Lớp 12 Toán 12 - Kết nối tri thức

Đề kiểm tra 15 phút Chương 1 Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số KNTT

Cùng nhau thử sức với bài kiểm tra 15 phút Toán 12 Kết nối tri thức Chương 1 Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số nhé!

  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Tìm tất cả các giá trị thực của tham số m để hàm số y = x^{3} - 3x^{2} + (m + 1)x + 2 có hai cực trị?

    Ta có: y' = 3x^{2} - 6x + m + 1

    Để hàm số đã cho có hai cực trị thì y' = 0 có hai nghiệm phân biệt

    \Rightarrow \Delta' > 0 \Leftrightarrow 9 - 3(m + 1) > 0 \Leftrightarrow m < 2

    Vậy với m < 2 thì hàm số y = x^{3} - 3x^{2} + (m + 1)x + 2 có hai cực trị.

  • Câu 2: Nhận biết

    Cho hàm số y = f(x) có đạo hàm f'(x) = x(x - 1)(x - 2);\forall x\mathbb{\in R}. Tìm số điểm cực đại của hàm số đã cho.

    Ta có: f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 1 \\ x = 2 \\ \end{matrix} ight.

    Ta có bảng xét dấu:

    Suy ra hàm số có một điểm cực đại.

  • Câu 3: Thông hiểu

    Cho hàm số y = f(x) xác định trên \mathbb{R}\backslash\left\{ 1 ight\} và có bảng biến thiên như sau:

    Số giá trị nguyên của tham số m để phương trình m - f(x) = 0 có ba nghiệm phân biệt là:

    Phương trình m - f(x) = 0 là phương trình hoành độ giao điểm của hai đồ thị (C):y = f(x) và đường thẳng (d):y = m

    Để phương trình m - f(x) = 0 có ba nghiệm phân biệt khi và chỉ khi (C);(d) có ba giao điểm \Leftrightarrow 1 < m < 4

    Mà m\mathbb{\in Z \Rightarrow}m \in \left\{ 2;3 ight\}

    Vậy có 2 giá trị nguyên của tham số m thỏa mãn điều kiện đề bài.

  • Câu 4: Thông hiểu

    Cho đồ thị hàm số y = f(x) như hình vẽ:

    Hàm số g(x) = 2f(x) + 2021 đồng biến trên khoảng:

    Ta có: g'(x) = 2f'(x) > 0 \Leftrightarrow f'(x) > 0

    \Leftrightarrow x \in ( - \infty; - 4) \cup (7; + \infty)

    Nên suy ra hàm số cũng đồng biến trên (8; + \infty).

  • Câu 5: Vận dụng

    Gọi m_{1};m_{2} là giá trị của tham số m để đồ thị hàm số y = 2x^{3} - 3x^{2} + m - 1 có hai điểm cực trị là P;Q sao cho diện tích tam giác OPQ bằng 2 (O là gốc tọa độ). Khi đó giá trị biểu thức m_{1}.m_{2} bằng:

    Tập xác định D\mathbb{= R}.

    Ta có: y' = 6x^{2} - 6x

    y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \Rightarrow y = m - 1 \\ x = 1 \Rightarrow y = m - 2 \\ \end{matrix} ight.

    Ta có bảng biến thiên như sau:

    Suy ra P(0;m - 1),Q(1;m - 2)

    \Rightarrow \overrightarrow{PQ} = (1; - 1) \Rightarrow \left| \overrightarrow{PQ} ight| = \sqrt{2}

    Đường thẳng (PQ) đi qua điểm P(0;m - 1) và nhận \overrightarrow{n} = (1;1) làm một vecto pháp tuyến nên có phương trình

    1(x - 0) + 1(y - m + 1) = 0 \Leftrightarrow x + y - m + 1 = 0

    d(O;PQ) = \frac{|1 - m|}{\sqrt{2}}

    Theo bài ra ta có diện tích tam giác OPQ bằng 2 nên ta có phương trình:

    S_{OAB} = \frac{1}{2}.d(O;PQ).PQ = 2

    \Leftrightarrow \frac{1}{2}.\frac{|1 - m|}{\sqrt{2}}.\sqrt{2} = 2 \Leftrightarrow |1 - m| = 4

    \Leftrightarrow \left\lbrack \begin{matrix} 1 - m = 4 \\ 1 - m = - 4 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} m = - 3 \\ m = 5 \\ \end{matrix} ight.

    Vậy m_{1}.m_{2} = - 15.

  • Câu 6: Thông hiểu

    Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật s(t) = t^{3} - 4t^{2} + 12(m), trong đó t(s) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc của chất điểm đó đạt giá trị bé nhất khi t bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật s(t) = t^{3} - 4t^{2} + 12(m), trong đó t(s) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc của chất điểm đó đạt giá trị bé nhất khi t bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 7: Nhận biết

    Cho hàm số y = f(x) có đạo hàm f'(x) trên khoảng ( - \infty; + \infty). Đồ thị hàm số y = f'(x) như hình vẽ:

    Hàm số y = f(x) nghịch biến trên khoảng nào trong các khoảng nào sau đây?

    Hàm số y = f(x) nghịch biến khi f'(x) \leq 0 \Leftrightarrow x \in (0;3)

    Vậy hàm số nghịch biến trên khoảng (0;3).

  • Câu 8: Thông hiểu

    Đồ thị hàm số y = \frac{x - 3}{x^{2} + x - 2} có bao nhiêu đường tiệm cận đứng?

    Ta có: y = \frac{x - 3}{x^{2} + x - 2} = \frac{x - 3}{(x - 1)(x + 2)}

    \lim_{x ightarrow 1^{+}}y = \lim_{x ightarrow 1^{+}}\frac{x - 3}{(x - 1)(x + 2)} = - \infty suy ra x = 1 là đường tiệm cận đứng của đồ thị hàm số.

    \lim_{x ightarrow 2^{+}}y = \lim_{x ightarrow 2^{+}}\frac{x - 3}{(x - 1)(x + 2)} = + \infty suy ra x = - 2 là đường tiệm cận đứng của đồ thị hàm số.

    Vậy đồ thị hàm số đã cho có 2 đường tiệm cận đứng.

  • Câu 9: Nhận biết

    Cho hàm số y =\frac{2x + 1}{x - 3}. Mệnh đề nào dưới đây là mệnh đề sai?

    Vì f'(x) = \frac{- 7}{(x - 3)^{2}}< 0;\forall x \in D nên đồ thị hàm số luôn nghịch biến trên các khoảng ( - \infty;3),(3; +\infty).

    Vậy mệnh đề sai là: "Hàm số đồng biến trên \mathbb{R}\backslash\left\{ 3 ight\}".

  • Câu 10: Vận dụng

    Hàm số y = \frac{1}{3}x^{3} + \frac{m}{2}x^{2} + x + 6 đồng biến trên nửa khoảng \lbrack 1; + \infty) khi:

    Ta có: y' = x^{2} + mx + 1

    Để hàm số đã cho đồng biến trên nửa khoảng \lbrack 1; + \infty) khi đó:

    \Leftrightarrow y' \geq 0;\forall x \in \lbrack 1; + \infty)

    \Leftrightarrow x^{2} + mx + 1 \geq 0;\forall x \in \lbrack 1; + \infty)

    \Leftrightarrow m \geq - x - \frac{1}{x};\forall x \in \lbrack 1; + \infty)

    Xét hàm số g(x) = - x - \frac{1}{x} trên nửa khoảng \lbrack 1; + \infty) ta có:

    g'(x) = - 1 + \frac{1}{x^{2}} = \frac{1 - x^{2}}{x^{2}}

    g'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 1 \\ \end{matrix} ight.

    Bảng biến thiên của hàm số g(x) = - x - \frac{1}{x} trên nửa khoảng \lbrack 1; + \infty) là:

    Từ bảng biến thiên suy ra \max_{\lbrack 1; + \infty)}g(x) = g(1) = - 2

    Vậy m \geq g(x);\forall x \in \lbrack 1; + \infty) khi và chỉ khi m \geq - 2.

  • Câu 11: Nhận biết

    Cho đồ thị hàm số như sau:

    Đồ thị hàm số đã cho có phương trình tiệm cận đứng và tiệm cận ngang lần lượt là:

    Dựa vào đồ thị hàm số ta thấy phương trình tiệm cận đứng và tiệm cận ngang của đồ thị hàm số lần lượt là x = - 1;y = 1.

  • Câu 12: Vận dụng

    Tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = \frac{1 + \sqrt{x + 1}}{x^{2} - 2x - m} có đúng hai tiệm cận đứng?

    Điều kiện xác định x \geq - 1

    Vì 1 + \sqrt{x + 1} > 0;\forall x \geq - 1 nên để đồ thị hàm số có đúng hai tiệm cận đứng thì phương trình x^{2} - 2x = m\ \ (*) phải có hai nghiệm phân biệt lớn hơn - 1.

    Xét hàm số f(x) = x^{2} - 2x trên \lbrack - 1; + \infty) có:

    f'(x) = 2x - 2 = 0 \Rightarrow x = 1

    Bảng biến thiên

    Phương trình (*) có hai nghiệm phân biệt lớn hơn - 1 khi - 1 < m \leq 3.

    Vậy đáp án cần tìm là m \in ( - 1;3brack.

  • Câu 13: Vận dụng cao

    Cho hàm số f(x) = x^{3} - 3x^{2} + m^{2} - 2m với m là tham số. Gọi S tập hợp tất cả các giá trị nguyên của tham số m thỏa mãn 3\max_{\lbrack - 3;1brack}f\left( |x| ight) + 2\min_{\lbrack - 3;1brack}f\left( |x| ight) \leq 112. Số phần tử của tập hợp S bằng:

    Ta có: f\left( |x| ight) = f\left( | - x| ight);\forall x\mathbb{\in R}

    \Rightarrow \left\{ \begin{matrix} \max_{\lbrack - 3;1brack}f\left( |x| ight) = \max_{0;3}f(x) \\ \min_{\lbrack - 3;1brack}f\left( |x| ight) = \min_{\lbrack 0;3brack}f(x) \\ \end{matrix} ight.

    Đạo hàm f'(x) = 3x^{2} - 6x = 0

    \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \Rightarrow f(0) = m^{2} - 2m \\ x = 2 \Rightarrow f(2) = m^{2} - 2m - 4 \\ \end{matrix} ight. và f(3) = m^{2} - 2m

    Suy ra 3\max_{\lbrack - 3;1brack}f\left( |x| ight) + 2\min_{\lbrack - 3;1brack}f\left( |x| ight) \leq 112

    \Leftrightarrow 3\left( m^{2} - 2m ight) + 2\left( m^{2} - 2m - 4 ight) \leq 112

    \Leftrightarrow m^{2} - 2m - 24 \leq 0 \Leftrightarrow - 4 \leq m \leq 6

    Mà m\mathbb{\in Z \Rightarrow}m \in \left\{ - 4; - 3;...;5;6 ight\}

    Vậy có tất cả 11 giá trị nguyên của tham số m.

  • Câu 14: Vận dụng

    Cho hàm số y = f(x) có đạo hàm f'\left( x ight) = {x^2} - 2x,\forall x \in \mathbb{R}. Hàm số g\left( x ight) = f\left( {2 - \sqrt {{x^2} + 1} } ight) - \sqrt {{x^2} + 1} - 3 đồng biến trên các khoảng nào?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) có đạo hàm f'\left( x ight) = {x^2} - 2x,\forall x \in \mathbb{R}. Hàm số g\left( x ight) = f\left( {2 - \sqrt {{x^2} + 1} } ight) - \sqrt {{x^2} + 1} - 3 đồng biến trên các khoảng nào?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 15: Thông hiểu

    Cho hàm số có đồ thị hàm số như hình vẽ.

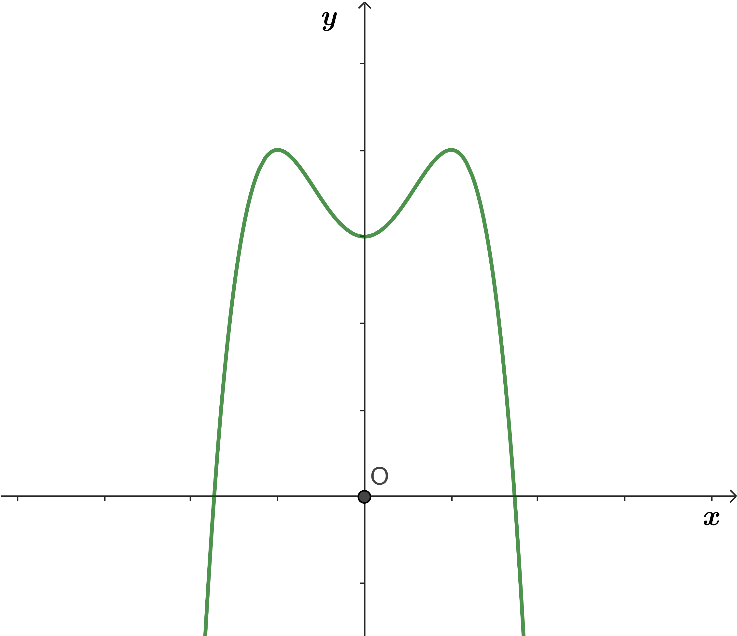
    Chọn khẳng định đúng trong các khẳng định dưới đây

    Chọn khẳng định đúng trong các khẳng định dưới đây?

    Dựa vào đồ thị hàm số ta thấy:

    \mathop {\lim }\limits_{x \to \infty } y = - \infty => Hệ số a < 0 => Loại đáp án C và D

    Đồ thị hàm số đi qua điểm \left( {0;d} ight) => d > 0

    Hàm số có ba cực trị => ab < 0

    Do a < 0 => b > 0

    Đồ thị hàm số đi qua điểm có tọa độ \left( {0;c} ight) => c > 0

  • Câu 16: Thông hiểu

    Hàm số y = f(x) = - x^{3} + 3x^{2} + (2m - 1)x - 1 nghịch biến trên khoảng (0; + \infty) khi và chỉ khi:

    Tập xác định D\mathbb{= R}

    Ta có:y' = - 3x^{2} + 6x + 2m - 1

    Hàm số đã cho nghịch biến trên khoảng (0; + \infty)

    y' \leq 0;\forall x \in (0; + \infty) khi và chỉ khi

    \Leftrightarrow 2m \leq 3x^{2} - 6x + 1;\forall x \in (0; + \infty)

    Xét hàm số g(x) = 3x^{2} - 6x + 1 trên (0; + \infty) ta có bảng biến thiên như sau:

    Dựa vào bảng biến thiên ta có:

    \min_{(0; + \infty)}g(x) = - 2

    Do đó \Leftrightarrow 2m \leq \min_{(0; + \infty)}g(x) \Leftrightarrow 2m \leq - 2 \Leftrightarrow m \leq - 1

    Vậy m \leq - 1 thỏa mãn yêu cầu bài toán.

  • Câu 17: Thông hiểu

    Có bao nhiêu giá trị nguyên của tham số m để hàm số y = \frac{x + 6}{x + 5m} nghịch biến trên khoảng (15; + \infty)?

    Tập xác định D\mathbb{= R}\backslash\left\{ - 5m ight\}

    Ta có: y' = \frac{5m - 6}{(x + 5m)^{2}}

    Hàm số y = \frac{x + 6}{x + 5m} nghịch biến trên khoảng (15; + \infty) khi và chỉ khi

    \left\{ \begin{matrix} 5m - 6 < 0 \\ - 5m \leq 15 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m < \frac{6}{5} \\ m \geq - 3 \\ \end{matrix} ight.\ \Leftrightarrow - 3 \leq m < \frac{6}{5}

    Vì m\mathbb{\in Z} nên có tất cả 5 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.

  • Câu 18: Nhận biết

    Cho hàm số y = \frac{3x - 1}{x + 2} có đồ thị kí hiệu là (H). Tìm điểm thuộc (H)?

    Ta thấy x = - 1 \Rightarrow y = \frac{3.( - 1) - 1}{( - 1) + 2} = - 4 \Rightarrow ( - 1; - 4) \in (H)

  • Câu 19: Vận dụng cao

    Cho hàm số y = \left| x^{3} - (2m +1)x^{2} + mx + m ight| với m là tham số. Giả sử S là tập hợp tất cả các giá trị nguyên của m \in \lbrack -2021;2021brack sao cho đồ thị của hàm số có 5 điểm cực trị. Tính tổng tất cả các phần tử của tập hợp S?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = \left| x^{3} - (2m +1)x^{2} + mx + m ight| với m là tham số. Giả sử S là tập hợp tất cả các giá trị nguyên của m \in \lbrack -2021;2021brack sao cho đồ thị của hàm số có 5 điểm cực trị. Tính tổng tất cả các phần tử của tập hợp S?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 20: Nhận biết

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Giá trị nhỏ nhất của hàm số đã cho trên đoạn \lbrack - 2;3brack bằng bao nhiêu?

    Giá trị nhỏ nhất của hàm số đã cho trên đoạn \lbrack - 2;3brack bằng - 3.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Chương 1 Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số KNTT Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án
Làm lại
  • 23 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Chương 1 Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số KNTT
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập