Lớp 10 Toán 10 - Kết nối tri thức

Đề kiểm tra 15 phút Chương 3 Hệ thức lượng trong tam giác

Đề kiểm tra 15 phút Toán 10 Chương 3 Hệ thức lượng trong tam giác sách Kết nối tri thức giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!

  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Vận dụng

    Cho tam giác ABC có góc A tù. Cho các biểu thức sau:

    (1) M = \sin A + \sin B + \sin C

    (2) N = \cos A.cosB.cosC

    (3) P = \cos\frac{A}{2}.sin\frac{B}{2}.cot\frac{C}{2}

    (4) Q = \cot A\tan B\cot C

    Số các biểu thức mang giá trị dương là:

    Ta có: A tù nên \cos A < 0;sinA > 0;tanA < 0;cotA < 0

    Do đó: M > 0;N < 0;P > 0;Q < 0.

  • Câu 2: Nhận biết

    Điểm cuối của \alpha thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?

    Điểm cuối của \alpha thuộc góc phần tư thứ hai ightarrow \left\{ \begin{matrix} \sin\alpha < 0 \\ \cos\alpha < 0 \\ \tan\alpha > 0 \\ \cot\alpha > 0 \\ \end{matrix} ight..

  • Câu 3: Nhận biết

    Trong các đẳng thức sau, đẳng thức nào đúng?

     Đáp án đúng là sin(180° – α) = sin α

  • Câu 4: Vận dụng

    Một tam giác có ba cạnh là 52,56,60. Bán kính đường tròn ngoại tiếp là:

    Ta có: p = \frac{a + b + c}{2} = \frac{52 + 56 + 60}{2} = 84.

    Suy ra: S = \sqrt{p(p - a)(p - b)(p - c)} = \sqrt{84(84 - 52)(84 - 56)(84 - 60)} = 1344.

    Mà S = \frac{abc}{4R} \Rightarrow R = \frac{abc}{4S} = \frac{52.56.60}{4.1344} = \frac{65}{2}.

  • Câu 5: Nhận biết

    Tam giác ABC có BC = 10 và \widehat{A}=30°. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

     Ta có: \frac {BC}{\sin A}=2R \Leftrightarrow R= \frac{BC}{2\sin A} =\frac {10}{2.sin30^{\circ} }=10.

  • Câu 6: Thông hiểu

    Bà Sáu sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150m, chiều dài của hàng rào MP là 230m. Góc giữa hai hàng rào MN và MP là 110^{\circ} (như hình vẽ)

    Diện tích mảnh đất mà gia đình bà Sáu sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?

    Diện tích mảnh đất của gia đình bà Sáu (tam giác MNP) là:

    S = \frac{1}{2}MN \cdot MP \cdot \sin M

    = \frac{1}{2} \cdot 150 \cdot 230 \cdot \sin110^{\circ} \approx 16209,7\left( {m}^{2}ight).

  • Câu 7: Thông hiểu

    Trong các đẳng thức sau, đẳng thức nào sai?

    Khẳng định sai là: "\sin {0^0} + \cos {0^0} = 0"

    Sửa lại là: "\sin {0^0} + \cos {0^0} = 1"

  • Câu 8: Thông hiểu

    Tam giác ABC có \widehat A = {105^0},\widehat B = {45^0};AC = 10. Độ dài cạnh AB là:

    Xét tam giác ABC ta có:

    \begin{matrix} \widehat A + \widehat B + \widehat C = {180^0} \hfill \\ \Rightarrow \widehat C = {180^0} - \left( {\widehat A + \widehat B} ight) = {30^0} \hfill \\ \end{matrix}

    Áp dụng định lí sin cho tam giác ABC ta có:

    \begin{matrix} \dfrac{{AC}}{{\sin \widehat B}} = \dfrac{{AB}}{{\sin \widehat C}} \hfill \\ \Rightarrow AB = \dfrac{{AC.\sin \widehat C}}{{\sin \widehat B}} = \dfrac{{10.\sin {{30}^0}}}{{\sin {{45}^0}}} = 5\sqrt 2 \hfill \\ \end{matrix}

  • Câu 9: Nhận biết

    Cho tam giác ABC có AB = 8 cm, AC = 18 cm và có diện tích bằng 64 cm^{2}. Giá trị sin A là:

    Ta có: 

    \begin{matrix} {S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \widehat A \hfill \\ \Rightarrow \sin \widehat A = \dfrac{{2S}}{{AB.AC}} = \dfrac{{2.64}}{{8.18}} = \dfrac{8}{9} \hfill \\ \end{matrix}

  • Câu 10: Nhận biết

    Cho tam giác ABC có a = 8,b = 10, góc C bằng 60^{0} . Độ dài cạnh c là ?

    Ta có: c^{2} = a^{2} + b^{2} - 2a.b.cosC = 8^{2} + 10^{2} - 2.8.10.cos60^{0} = 84 \Rightarrow c = 2\sqrt{21}.

  • Câu 11: Thông hiểu

    Cho tam giác ABC thỏa mãn BC^{2} + AC^{2} - AB^{2} - \sqrt{2}BC.AC = 0. Khi đó, góc C có số đo là:

    Theo đề bài ra ta có:

    BC^{2} + AC^{2} - AB^{2} - \sqrt{2}BC.AC = 0

    \Leftrightarrow BC^{2} + AC^{2} - AB^{2} = \sqrt{2}BC.AC

    \Leftrightarrow \frac{BC^{2} + AC^{2} - AB^{2}}{BC \cdot AC} = \sqrt{2}

    \Leftrightarrow 2\cos C - \sqrt{2} = 0

    \Leftrightarrow \cos C = \frac{\sqrt{2}}{2}\Rightarrow \widehat{C} = 45^{\circ}.

  • Câu 12: Thông hiểu

    Giá trị biểu thức S = {\cos ^2}{12^0} + {\cos ^2}{48^0} + {\cos ^2}{1^0} + {\cos ^2}{89^0} bằng:

    Ta có:

    \begin{matrix} S = {\cos ^2}{12^0} + {\cos ^2}{48^0} + {\cos ^2}{1^0} + {\cos ^2}{89^0} \hfill \\ = {\cos ^2}{12^0} + {\sin ^2}{12^0} + {\cos ^2}{1^0} + {\sin ^2}{1^0} \hfill \\ = 1 + 1 = 2 \hfill \\ \end{matrix}

  • Câu 13: Nhận biết

    Tam giác ABC có \widehat{B} = 60{^\circ},\ \ \widehat{C} = 45{^\circ} và AB = 5. Tính độ dài cạnh AC.

    Theo định lí hàm sin, ta có \frac{AB}{\sin\widehat{C}} = \frac{AC}{\sin\widehat{B}} \Leftrightarrow \frac{5}{sin45{^\circ}} = \frac{AC}{sin60{^\circ}} \Rightarrow AC = \frac{5\sqrt{6}}{2}.

  • Câu 14: Thông hiểu

    Giá trị biểu thức A = \sin {30^0}.\cos {60^0} + \sin {60^0}.\cos {30^0} là:

    Ta có:

    \begin{matrix} A = \sin {30^0}.\cos {60^0} + \sin {60^0}.\cos {30^0} \hfill \\ A = \dfrac{1}{2}.\dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{2} \hfill \\ A = \dfrac{1}{4} + \dfrac{3}{4} = 1 \hfill \\ \end{matrix}

  • Câu 15: Nhận biết

    Tam giác ABC có AB=5,BC=7,CA=8. Số đo góc \hat A bằng:

     Áp dụng định lí côsin:

    \cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}}= \frac{{{5^2} + {8^2} - {7^2}}}{{2.5.8}} = \frac{1}{2}.

    Suy ra \hat A = 60^{\circ}.

  • Câu 16: Vận dụng

    Tính giá trị của \cos\left\lbrack \frac{\pi}{4} + (2k + 1)\pi ightbrack.

    Ta có \cos\left\lbrack \frac{\pi}{4} + (2k + 1)\pi ightbrack = \cos\left( \frac{5\pi}{4} + 2k\pi ight) = \cos\frac{5\pi}{4}

    = \cos\left( \pi + \frac{\pi}{4} ight) = - \cos\frac{\pi}{4} = - \frac{\sqrt{2}}{2}.

  • Câu 17: Nhận biết

    Cho \Delta ABC có b = 6,c = 8,\widehat{A} = 60^{0}. Độ dài cạnh a là:

    Ta có: a^{2} = b^{2} + c^{2} - 2bc\cos A = 36 + 64 - 2.6.8.cos60^{0} = 52

    \Rightarrow a = 2\sqrt{13}.

  • Câu 18: Thông hiểu

    Điểm cuối của góc lượng giác \alpha ở góc phần tư thứ mấy nếu \sin\alpha,\ tan\alpha trái dấu?

    Điểm cuối của \alpha thuộc góc phần tư thứ hai thì \sin\alpha > 0, \cos\alpha < 0.

    Điểm cuối của \alpha thuộc góc phần tư thứ tư thì \sin\alpha < 0, \cos\alpha > 0.

    Vậy nếu \sin\alpha,\ cos\alpha trái dấu thì điểm cuối của góc lượng giác \alpha ở góc phần tư thứ II hoặc IV.

  • Câu 19: Thông hiểu

    Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và \widehat{ACB} = 60{^\circ}. Tính độ dài cạnh cạnh BC.

    Gọi M,\ \ N lần lượt là trung điểm của AB,\ \ BC.

    \overset{}{ightarrow}MN là đường trung bình của \Delta ABC.

    \overset{}{ightarrow}MN = \frac{1}{2}AC. Mà MN = 3, suy ra AC = 6.

    Theo định lí hàm cosin, ta có:

    AB^{2} = AC^{2} + BC^{2} - 2.AC.BC.cos\widehat{ACB}

    \Leftrightarrow 9^{2} = 6^{2} + BC^{2} - 2.6.BC.cos60{^\circ}

    \Rightarrow BC = 3 + 3\sqrt{6}

  • Câu 20: Vận dụng

    Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30' (hình vẽ).

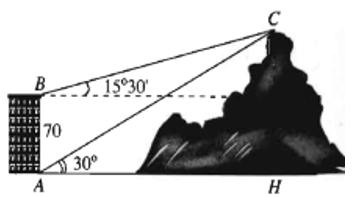
    Tính độ cao CH của ngọn núi

    Ngọn núi đó có độ cao CH so với mặt đất gần nhất với giá trị nào sau đây?

    Ta có: \widehat {ABC} = {90^0} + {15^0}30' = {105^0}30'

    Xét tam giác ABC ta có:

    \begin{matrix} \widehat {ABC} + \widehat {CAB} + \widehat {ACB} = {180^0} \hfill \\ \Rightarrow \widehat {ACB} = {180^0} - \left( {\widehat {ABC} + \widehat {CAB}} ight) \hfill \\ \Rightarrow \widehat {ACB} = {180^0} - \left( {{{105}^0}30\prime + {{60}^0}} ight) \hfill \\ \Rightarrow \widehat {ACB} = {14^0}30\prime \hfill \\ \end{matrix}

    Áp dụng định lí sin cho tam giác ABC ta có:

    \begin{matrix} \dfrac{{AB}}{{\sin \widehat {ACB}}} = \dfrac{{AC}}{{\sin \widehat {ABC}}} \hfill \\ \Rightarrow AC = \dfrac{{AB.\sin \widehat {ABC}}}{{\sin \widehat {ACB}}} \hfill \\ \Rightarrow AC = \dfrac{{70.\sin {{107}^0}30'}}{{\sin {{14}^0}30'}} \approx 269,4\left( m ight) \hfill \\ \end{matrix}

    Xét tam giác ACH vuông tại H ta có:

    \begin{matrix} CH = AC.\sin \widehat {CAH} \hfill \\ \Rightarrow CH \approx 269,4.\sin {30^0} \approx 134,7\left( m ight) \hfill \\ \end{matrix}

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Chương 3 Hệ thức lượng trong tam giác Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 27 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Chương 3 Hệ thức lượng trong tam giác
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập