Lớp 12 Toán 12 - Chân trời sáng tạo

Đề kiểm tra 15 phút Chương 5 Phương trình mặt phẳng, đường thẳng, mặt cầu CTST

Cùng nhau thử sức với bài kiểm tra 15 phút Toán 12 Chân trời sáng tạo Chương 5 Phương trình mặt phẳng, đường thẳng, mặt cầu nhé!

  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x + 2y - 2z + 1 = 0 và (Q):x + my + (m - 1)z + 2019 = 0. Khi hai mặt phẳng (P), (Q) tạo với nhau một góc nhỏ nhất thì mặt phẳng (Q) đi qua điểm M nào sau đây?

    Gọi \alpha là góc giữa (P) và (Q).

    Ta có:

    \cos\alpha = \dfrac{\left|{\overrightarrow{n}}_{P} \cdot {\overrightarrow{n}}_{Q} ight|}{\left|{\overrightarrow{n}}_{P} ight| \cdot \left| {\overrightarrow{n}}_{Q}ight|}= \dfrac{1}{3\sqrt{2m^{2} - 2m + 2}} = \dfrac{1}{3\sqrt{2\left( m- \dfrac{1}{2} ight)^{2} + \dfrac{3}{2}}}

    \leq \dfrac{1}{3\sqrt{2\left( m -\dfrac{1}{2} ight)^{2} + \dfrac{3}{2}}} \leq\dfrac{1}{3\sqrt{\dfrac{3}{2}}}

    Do 0 \leq \alpha \leq 90^{\circ} nên \alpha nhỏ nhất khi \cos\alpha lớn nhất \Leftrightarrow m = \frac{1}{2}.

    \Rightarrow (Q):2x + y - z + 4038 = 0 \Rightarrow M( - 2019;1;1) \in (Q).

  • Câu 2: Vận dụng

    Trong không gian với hệ tọa độ Oxyz, cho ba đường thẳng d:\frac{x}{1} = \frac{y}{1} = \frac{z + 1}{-2},\Delta_{1}:\frac{x - 3}{2} = \frac{y}{1} = \frac{z -1}{1},\Delta_{2}:\frac{x - 1}{1} = \frac{y - 2}{2} =\frac{z}{1}. Đường thẳng \Delta vuông góc với d đồng thời cắt \Delta_{1};\Delta_{2} tương ứng tại H;K sao cho độ dài HK nhỏ nhất. Biết rằng \Delta có một vectơ chỉ phương \overrightarrow{u} = (h;\ k;\ 1). Giá trị h - k bằng?

    Ta có \left\{ \begin{matrix} H \in \Delta_{1} \Leftrightarrow H(3 + 2t;t;1 + t) \\ K \in \Delta_{2} \Leftrightarrow K(1 + m;2 + 2m;m) \\ \end{matrix} ight.

    Suy ra \overrightarrow{HK} = (m - 2t - 2;2m - t + 2;m - t - 1)

    Đường thẳng d có một VTCP là \overrightarrow{u_{d}} = (1;1; - 2)

    \Delta\bot d \Rightarrow \overrightarrow{u_{d}}.\overrightarrow{HK} = 0

    \Leftrightarrow \ m - t + 2 = 0 \Leftrightarrow m = t - 2

    \Rightarrow \overrightarrow{HK} = ( - t - 4;t - 2; - 3)

    Ta có: HK^{2} = ( - t - 4)^{2} + (t - 2)^{2} + ( - 3)^{2} = 2(t + 1)^{2} + 27 \geq 27;\forall t\mathbb{\in R}

    \Rightarrow \min HK = \sqrt{27} khi và chỉ khi t = - 1

    \Rightarrow \overrightarrow{HK} = ( - 3; - 3; - 3) \Rightarrow \overrightarrow{u} = (1;1;1)

    \Rightarrow h = k = 1 \Rightarrow h - k = 0

  • Câu 3: Vận dụng

    Trong không gian Oxyz cho điểm M(2;1;5). Mặt phẳng (P) đi qua điểm M và cắt các trục Ox,Oy,Oz lần lượt tại các điểm A,B,C sao cho M là trực tâm của tam giác ABC. Tính khoảng cách từ điểm I(1;2;3) đến mặt phẳng (P).

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Trong không gian Oxyz cho điểm M(2;1;5). Mặt phẳng (P) đi qua điểm M và cắt các trục Ox,Oy,Oz lần lượt tại các điểm A,B,C sao cho M là trực tâm của tam giác ABC. Tính khoảng cách từ điểm I(1;2;3) đến mặt phẳng (P).

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 4: Nhận biết

    Trong không gian Oxyz cho hai điểm A(2;0; - 1),B(1;1;0) và (\alpha) là mặt phẳng trung trực của đoạn thẳng AB. Vectơ nào sau đây là một vectơ pháp tuyến của (\alpha)?

    Do (\alpha) là mặt phẳng trung trực của đoạn thẳng AB nên (\alpha) nhận \overrightarrow{AB} = ( - 1;1;1) làm vectơ pháp tuyến.

    Suy ra \overrightarrow{n}(1; - 1; - 1) = - \overrightarrow{AB} cũng là vectơ pháp tuyến của (α).

  • Câu 5: Thông hiểu

    Trong không gian với hệ tọa độ Oxyz, cho các điểm A( - 1;0;0),B(0;0;2),C(0; - 3;0). Bán kính mặt cầu ngoại tiếp tứ diện OABC là:

    Gọi (S) là mặt cầu ngoại tiếp tứ diện OABC

    Phương trình mặt cầu (S) có dạng x^{2} + y^{2} + z^{2} - 2ax - 2by - 2cz + d = 0

    Vì O;A;B;C \in (S) nên ta có: \left\{ \begin{matrix} d = 0 \\ 1 + 2a + d = 0 \\ 4 - 4c + d = 0 \\ 9 + 6b + d = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} d = 0 \\ a = - \frac{1}{2} \\ b = - \frac{3}{2} \\ c = 1 \\ \end{matrix} ight.

    Vậy bán kính mặt cầu (S) là:

    R = \sqrt{a^{2} + b^{2} + c^{2} - d} = \sqrt{\frac{1}{4} + \frac{9}{4} + 1} = \frac{\sqrt{14}}{2}

  • Câu 6: Nhận biết

    Trong không gian Oxyz, cho mặt phẳng (P):x - 2y - 3z - 2 = 0. Đường thẳng d vuông góc với mặt phẳng (P) có một vectơ chỉ phương có tọa độ là:

    Mặt phẳng (P) có một vectơ pháp tuyến là \overrightarrow{n} = (1; - 2; - 3).

    Do d\bot(P) nên vectơ \overrightarrow{n} = (1; - 2; - 3) cũng là một vectơ chỉ phương của d.

  • Câu 7: Nhận biết

    Trong không gian Oxyz, phương trình nào sau đây là phương trình của mặt cầu có tâm I(7;6; - 5) và bán kính 9?

    Mặt cầu tâm I(7;6; - 5), bán kính R = 9 có phương trình lá:

    (x - 7)^{2} + (y - 6)^{2} + (z - 5)^{2} = 81.

  • Câu 8: Thông hiểu

    Trong không gian Oxyz, cho điểm A(0;1;1) và hai đường thẳng d_{1}:\left\{ \begin{matrix} x = - 1 \\ y = - 1 + t \\ z = t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight) và d_{2}:\frac{x - 1}{3} = \frac{y - 2}{1} = \frac{z}{1}. Gọi d là đường thẳng đi qua điểm A, cắt đường thẳng d_{1} và vuông góc với đường thẳng d_{2}. Đường thẳng d đi qua điểm nào trong các điểm dưới đây?

    Gọi \left\{ \begin{matrix} B = d_{1} \cap d \\ B \in d_{1} \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} B( - 1; - 1 + t;t) \\ \overrightarrow{AB} = ( - 1;t - 2;t - 1) \\ \end{matrix} ight.

    d_{2} có một vectơ chỉ phương \overrightarrow{u} = (3;1;1).

    Do d\bot d_{2} nên \overrightarrow{u}.\overrightarrow{AB} = 0 \Leftrightarrow - 3 + t - 2 + t - 1 = 0

    \Leftrightarrow t = 3 \Rightarrow \overrightarrow{AB} = ( - 1;1;2)

    Ta có: \left\{ \begin{matrix} \overrightarrow{AN} = (2;0;6);\overrightarrow{AQ} = (3;1;4) \\ \overrightarrow{AP} = ( - 2; - 4;10);\overrightarrow{AM} = (1; - 1; - 2) \\ \end{matrix} ight.

    Suy ra đường thẳng d đi qua M.

  • Câu 9: Vận dụng cao

    Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: \dfrac{x-2}{2}=\dfrac{y}{-1} = \dfrac z 4và mặt

    cầu (S) tâm I(1;2;1), bán kính R. Hai mặt phẳng (P) và (Q) chứa d và tiếp xúc với

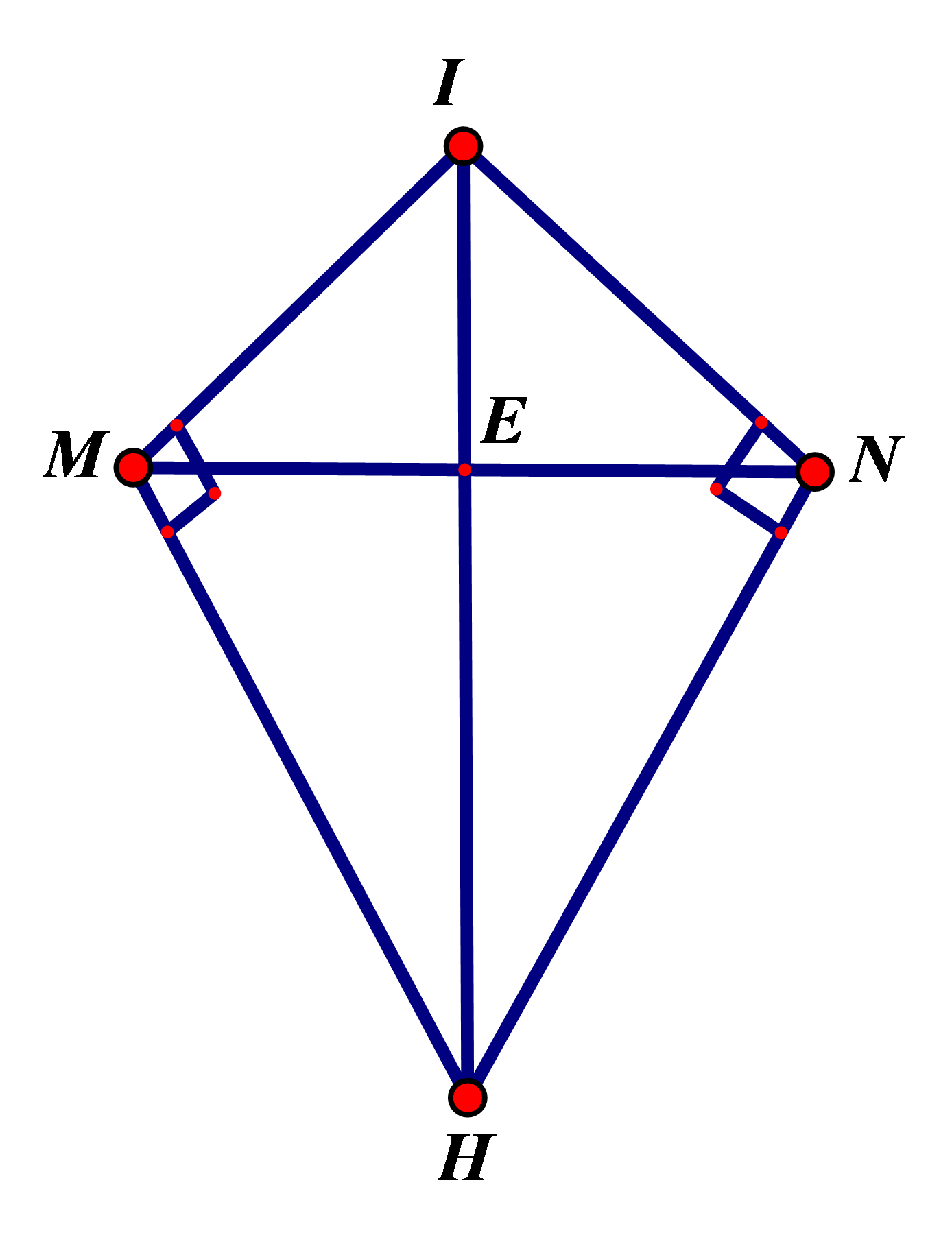
    (S) tạo với nhau góc 60^0 . Hãy viết phương trình mặt cầu (S)

     Viết phương trình mặt cầu

    Gọi M, N là tiếp điểm của mặt phẳng (P), (Q) và mặt cầu (S). Gọi H là hình chiếu của điểm I trên đường thẳng d.

    \Rightarrow IH=d(I,d)= \sqrt 6

    TH1: Góc \widehat {MHN}=60^0:

    Theo bài ra ta có: R=IM=IH.\sin30^0= \sqrt 6 .\frac 1 2 = \frac{\sqrt 6}{2}

    \Rightarrow(S) : (x-1)^2+(y-2)^2+(z-1)^2= \frac 3 2

    TH2: Góc \widehat {MHN}=120^0:

    Theo bài ra ta có: R=IM=IH.\sin60^0= \sqrt 6 .\frac {\sqrt 3}{2} = \frac{\sqrt18}{2}

    \Rightarrow(S) : (x-1)^2+(y-2)^2+(z-1)^2= \frac 9 2.

  • Câu 10: Vận dụng

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông có độ dài đường chéo bằng a\sqrt{2} và SA vuông góc với mặt phẳng (ABCD). Gọi α là góc giữa hai mặt phẳng (SBD) và (ABCD). Nếu \tan\alpha = \sqrt{2} thì góc giữa hai mặt phẳng (SAC) và (SBC) bằng:

    Hình vẽ minh họa

    Gọi I = AC \cap BD.

    Hình vuông ABCD có độ dài đường chéo bằng a\sqrt{2} suy ra hình vuông đó có cạnh bằng a.

    Ta có \left\{ \begin{matrix} (SBD) \cap (ABCD) = BD \\ SI\bot BD \\ AI\bot BD \\ \end{matrix} \Rightarrow ((SBD);(ABCD)) = (SI;AI) = SIA ight..

    Ta có tan\alpha = tanSIA = \frac{SA}{AI} \Leftrightarrow SA = a.

    Chọn hệ trục tọa độ Oxyz như hình vẽ. Ta có A(0;0;0),B(a;0;0),C(a;a;0),S(0;0;a).

    Khi đó \overrightarrow{SA} = (0;0; - a);\overrightarrow{SC} = (a;a; - a);\overrightarrow{SB} = (a;0; - a).

    Mặt phẳng (SAC) có vectơ pháp tuyến {\overrightarrow{n}}_{1} = ( - 1;1;0).

    Mặt phẳng (SBC) có vectơ pháp tuyến {\overrightarrow{n}}_{2} = (1;0;1).

    Suy ra cos((SAC);(SBC)) = \frac{\left|{\overrightarrow{n}}_{1} \cdot {\overrightarrow{n}}_{2} ight|}{\left|{\overrightarrow{n}}_{1} ight| \cdot \left| {\overrightarrow{n}}_{2}ight|}= \frac{1}{\sqrt{2} \cdot \sqrt{2}} = \frac{1}{2}\Rightarrow((SAC);(SBC)) = 60^{\circ}.

  • Câu 11: Nhận biết

    Trong không gian Oxyz, hai điểm A(7; - 2;2) và B(1;2;4). Phương trình nào sau đây là phương trình mặt cầu đường kính AB?

    Mặt cầu nhận AB làm đường kính, do đó mặt cầu nhận trung điểm I(4;0;3) của AB làm tâm và có bán kính R = \frac{AB}{2} = \sqrt{56}

    Suy ra phương trình mặt cầu cần tìm là (x - 4)^{2} + y^{2} + (z - 3)^{2} = 56.

  • Câu 12: Thông hiểu

    Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;6; - 7);B(3;2;1). Phương trình mặt phẳng trung trực của đoạn thẳng AB là:

    Gọi (P) là mặt phẳng trung trực của đoạn thẳng AB.

    Ta có \overrightarrow{AB} = (2; - 4;8)

    Suy ra một vectơ pháp tuyến của (P) là \overrightarrow{n_{(P)}} = (1; - 2;4)

    Hơn nữa, trung điểm của AB là I(2; 4; −3) thuộc mặt phẳng (P) nên

    (P):(x - 2) - 2(y - 4) + 4(z + 3) = 0

    \Leftrightarrow x - 2y + 4z + 18 = 0.

  • Câu 13: Nhận biết

    Trong không gian Oxyz đường thẳng \Delta:\frac{x}{1} = \frac{y}{2} = \frac{z}{- 1} = 1 và mặt phẳng (\alpha):x - y + 2z = 0. Góc giữa mặt phẳng (\alpha) và đường thẳng \Delta bằng:

    Mặt phẳng (\alpha):x - y + 2z = 0 có một vectơ pháp tuyến là \overrightarrow{n} = (1; - 1;2)

    Đường thẳng \Delta:\frac{x}{1} = \frac{y}{2} = \frac{z}{- 1} = 1 có một vectơ chỉ phương là \overrightarrow{u} = (1;2; - 1)

    Gọi α là góc giữa đường thẳng \Delta và mặt phẳng (\alpha):

    \sin\alpha = \left| \cos\alpha ight| = \frac{\left| \overrightarrow{u}.\overrightarrow{n} ight|}{\left| \overrightarrow{u} ight|.\left| \overrightarrow{n} ight|} = \frac{|1 - 2 - 2|}{\sqrt{6}.\sqrt{6}} = \frac{1}{2} \Rightarrow \alpha = 30^{0}

  • Câu 14: Vận dụng cao

    Cho hai đường thẳng (d1 ): \left\{ \begin{array}{l}x - y + z - 5 = 0\\x - 3y + 6 = 0\end{array} ight. và ({d_2})\left\{ \begin{array}{l}2y + z - 5 = 0\\4x - 2y + 5z - 4 = 0\end{array} ight.

    Xét VTTĐ của (d1 ) và (d2 )? Tìm câu đúng ?

    Chuyển đường thẳng (d1 ) và (d2 ) về dạng tham số :

    ({d_1}):\left\{ \begin{array}{l}x = - 6 + 3t\\y = t\\z = 11 - 2t\end{array} ight. \Rightarrow ({d_1}) có vectơ chỉ phương \overrightarrow a = (3,1, - 2) và qua A( - 6,0,11) .

    ({d_2}):\left\{ \begin{array}{l}x = \frac{{15}}{4} - 3t'\\y = 3 - t'\\z = - 1 + 2t'\end{array} ight. \Rightarrow \left( {{d_2}} ight) có vectơ chỉ phương \overrightarrow b = (\frac{{15}}{4},3, - 1)

    \overrightarrow a earrow \swarrow \overrightarrow bvà hệ phương trình \left\{ \begin{array}{l} - 6 + 3t = \frac{{15}}{4} - 3t'\\t = 3 - t'\\11 - 2t = - 1 + 2t'\end{array} ight. vô nghiệm.

    \Rightarrow ({d_1})//(d_{2} ).

  • Câu 15: Thông hiểu

    Trong không gian với tọa độ Oxyz cho A(2; - 3;0) và mặt phẳng (\alpha):x + 2y - z + 3 = 0. Tìm phương trình mặt phẳng (P) đi qua A sao cho (P) vuông góc với (α) và (P) song song với trục Oz?

    Vì (P)\bot(\alpha) nên \overrightarrow{n_{(P)}}\bot\overrightarrow{n_{(\alpha)}} và (P)//Oz nên \overrightarrow{n_{(P)}}\bot\overrightarrow{k}

    Chọn \overrightarrow{n_{(P)}} = \left\lbrack \overrightarrow{n_{(\alpha)}};\overrightarrow{k} ightbrack = (2; - 1;0)

    Phương trình mặt phẳng (P) là 2x - y - 7 = 0.

  • Câu 16: Thông hiểu

    Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \Delta:\frac{x - 1}{1} = \frac{y - 2}{3} = \frac{z - 3}{- 1}. Gọi ∆’ là đường thẳng đối xứng với đường thẳng ∆ qua (Oxy). Tìm một vectơ chỉ phương của đường thẳng ∆’.

    Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm A(4; 11; 0).

    Ta thấy B(1; 2; 3) ∈ ∆ và B’(1; 2; −3) là điểm đối xứng của điểm B qua mặt phẳng (Oxy).

    Đường thẳng ∆’ đi qua các điểm A, B’.

    Ta có \overrightarrow{AB} = ( - 3; - 9; - 3), từ đó suy ra \overrightarrow{u} = (1;3;1) là một vectơ chỉ phương của đường thẳng ∆’.

  • Câu 17: Nhận biết

    Trong không gian tọa độ Oxyz, cho đường thẳng \Delta:\frac{x - 1}{- 2} = \frac{y + 1}{2} = \frac{z - 2}{- 1} và mặt phẳng (P):2x - y - 2z + 1 = 0. Gọi \alpha là góc giữa đường thẳng \Delta và mặt phẳng (P). Khẳng định nào sau đây đúng?

    Ta có: \Delta có một vectơ chỉ phương là \overrightarrow{u} = ( - 2;2; - 1), (P) có một vectơ pháp tuyến là \overrightarrow{n} = (2; - 1; - 2).

    Từ đó: \sin\alpha = \left| \cos\left( \overrightarrow{n};\overrightarrow{u} ight) ight| = \left| \frac{\overrightarrow{n}.\overrightarrow{u}}{\left| \overrightarrow{n} ight|.\left| \overrightarrow{u} ight|} ight| = \frac{4}{9}

  • Câu 18: Thông hiểu

    Trong không gian Oxyz, cho mặt cầu (S):(x + 3)^{2} + (y - 1)^{2} + (z + 1)^{2} = 3 và mặt phẳng (\alpha):(m - 4)x + 3y - 3mz + 2m - 8 = 0. Với giá trị nào của tham số m thì mặt phẳng tiếp xúc với mặt cầu?

    Mặt cầu (S) có tâm I(−3; 1; −1) và bán kính R = \sqrt{3}

    Mặt phẳng (α) tiếp xúc với (S) khi và chỉ khi

    d\left( I;(P) ight) = R

    \Leftrightarrow \frac{\left| (m - 4).( - 3) + 3.1 - 3m.( - 1) + 2m - 8 ight|}{\sqrt{(m - 4)^{2} + 3^{2} + ( - 3m)^{2}}} = \sqrt{3}

    \Leftrightarrow \frac{|2m + 7|}{\sqrt{10m^{2} - 8m + 25}} = \sqrt{3}

    \Leftrightarrow 26m^{2} - 52m + 26 = 0 \Leftrightarrow m = 1

    Vậy đáp án cần tìm là: m = 1.

  • Câu 19: Nhận biết

    Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (\alpha):x - y + 2z = 1. Trong các đường thẳng sau, đường thẳng nào vuông góc với (\alpha).

    Mặt phẳng (\alpha):x - y + 2z = 1 có một vectơ pháp tuyến là \overrightarrow{n_{(\alpha)}} = (1; - 1;2).

    Đường thẳng d_{1} có một vectơ chỉ phương là \overrightarrow{u_{d_{1}}} = (1; - 1;2) = \overrightarrow{n_{(\alpha)}}

    Suy ra d_{1}\bot(\alpha).

  • Câu 20: Nhận biết

    Câu nào sau đây đúng? Trong không gian Oxyz:

     A sai và có thể (P) và (Q) trùng nhau

    B sai, vì mỗi mặt phẳng có vô số vecto pháp tuyến. Suy ra D sai.

    C đúng vì 1 mặt phẳng được xác định nếu biết một điểm và một VTPT của nó.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Chương 5 Phương trình mặt phẳng, đường thẳng, mặt cầu CTST Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án
Làm lại
  • 12 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Chương 5 Phương trình mặt phẳng, đường thẳng, mặt cầu CTST
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập