Lớp 12 Toán 12

Đề kiểm tra 15 phút Hàm số lũy thừa

Cùng nhau thử sức với bài kiểm tra 15 phút Hàm số lũy thừa

  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Tính đạo hàm của hàm số y = \left( {{x^2} + 2x - 2} ight){.5^x}

     Ta có:

    \begin{matrix} y' = \left( {{x^2} + 2x - 2} ight)'{.5^x} + \left( {{5^x}} ight)'.\left( {{x^2} + 2x - 2} ight) \hfill \\ \Rightarrow y' = \left( {2x + 2} ight){.5^x} + \left( {{x^2} + 2x - 2} ight){.5^x}.\ln 5 \hfill \\ \end{matrix}

  • Câu 2: Vận dụng

    Cho {9^x} + {9^{ - x}} = 14;\frac{{6 + 3.\left( {{3^x} + {3^{ - x}}} ight)}}{{2 - {3^{x + 1}} - {3^{1 - x}}}} = \frac{a}{b}; (\frac{a}{b} là phân số tối giản). Tính giá trị biểu thức P = ab.

    Ta có:

    \begin{matrix} {\left( {{3^x} + {3^{ - x}}} ight)^2} = 14 + 2 = 16 \hfill \\ \Rightarrow {3^x} + {3^{ - x}} = 4 \hfill \\ \Rightarrow \dfrac{a}{b} = \dfrac{{6 + 3.4}}{{2 - 3.4}} = - \dfrac{9}{5} \hfill \\ \Rightarrow P = - 45 \hfill \\ \end{matrix}

  • Câu 3: Thông hiểu

    Cho số thực a dương. Rút gọn biểu thức P = \sqrt[5]{{a.\sqrt[4]{{a.\sqrt[3]{{a\sqrt a }}}}}}

    Ta có:

    P = \sqrt[5]{{a.\sqrt[4]{{a.\sqrt[3]{{{a^{\frac{3}{2}}}}}}}}} = {\left( {a\sqrt[4]{{a.{a^{\frac{1}{2}}}}}} ight)^{\frac{1}{5}}} = {\left( {a\sqrt[4]{{{a^{\frac{3}{2}}}}}} ight)^{\frac{1}{5}}} = {\left( {a.{a^{\frac{3}{8}}}} ight)^{\frac{1}{5}}} = {\left( {{a^{\frac{{11}}{8}}}} ight)^{\frac{1}{5}}} = {a^{\frac{{11}}{{40}}}}

  • Câu 4: Nhận biết

    Giá trị của biểu thức P = {\left( {1 + \sqrt 3 } ight)^{2016}}.{\left( {3 - \sqrt 3 } ight)^{2016}} bằng:

    Ta có:

    P = {\left( {1 + \sqrt 3 } ight)^{2016}}.{\left( {3 - \sqrt 3 } ight)^{2016}}

    = {\left[ {\left( {1 + \sqrt 3 } ight)\left( {3 - \sqrt 3 } ight)} ight]^{2016}} = {\left( {2\sqrt 3 } ight)^{2016}} = {12^{1008}}

  • Câu 5: Nhận biết

    Biết \frac{{{x^{{a^2}}}}}{{{x^{{b^2}}}}} = {x^{16}} với x > 1 và a + b = 2. Tính giá trị của biểu thức M = a – b.

     Ta có: 

    \begin{matrix} \dfrac{{{x^{{a^2}}}}}{{{x^{{b^2}}}}} = {x^{16}} \hfill \\ \Leftrightarrow {x^{{a^2} - {b^2}}} = {x^{16}} \hfill \\ \Leftrightarrow {a^2} - {b^2} = 16 \hfill \\ \Leftrightarrow \left( {a + b} ight)\left( {a - b} ight) = 16 \hfill \\ \Rightarrow a - b = 8 \hfill \\ \end{matrix}

  • Câu 6: Nhận biết

    Cho biết Q = \sqrt {{a^2}.\sqrt[3]{{{a^4}}}} với a > 0,a e 1. Chọn khẳng định đúng?

    Ta có: Q = \sqrt {{a^2}.\sqrt[3]{{{a^4}}}} = {\left( {{a^2}.{a^{\frac{4}{3}}}} ight)^{\frac{1}{2}}} = {\left( {{a^{\frac{{10}}{3}}}} ight)^{\frac{1}{2}}} = {a^{\frac{5}{3}}}

    Vậy Q = {a^{\frac{5}{3}}}

  • Câu 7: Vận dụng

    Cho x > 0;y > 0. Viết biểu thức {x^{\frac{4}{5}}}.\sqrt[6]{{{x^5}\sqrt x }} = {x^m} và {y^{\frac{4}{5}}}:\sqrt[6]{{{y^5}\sqrt y }} = {y^n}. Tính T = m - n

    Ta có:

    \left\{ {\begin{array}{*{20}{c}} {{{\left( {{x^m}} ight)}^6} = {x^{\frac{{24}}{5}}}.{x^5}.{x^{\frac{1}{2}}} = {x^{\frac{{103}}{{10}}}} \Rightarrow m = \dfrac{{103}}{{60}}} \\ {{{\left( {{y^n}} ight)}^6} = {y^{\frac{{24}}{5}}}:\left( {{y^5}.{y^{\frac{1}{2}}}} ight) = {y^{ - \frac{7}{{10}}}} \Rightarrow n = - \dfrac{7}{{60}}} \end{array}} ight. \Rightarrow T = m - n = \frac{{11}}{6}

  • Câu 8: Vận dụng cao

    Cho P = \sqrt {{x^2} + \sqrt[3]{{{x^4}{y^2}}}} + \sqrt {{y^2} + \sqrt[3]{{{x^2}{y^4}}}} và Q = 2\sqrt {{{\left( {\sqrt[3]{{{x^2}}} + \sqrt[3]{{{y^2}}}} ight)}^3}} với x và y là các số thực khác 0. So sánh P và Q?

    Ta có: {x^2};{y^2};\sqrt[3]{{{x^4}{y^2}}};\sqrt[3]{{{x^2}{y^4}}} là những số thực dương

    Ta lại có:

    \begin{matrix} Q = 2\sqrt {{{\left( {\sqrt[3]{{{x^2}}} + \sqrt[3]{{{y^2}}}} ight)}^3}} \hfill \\ = 2\sqrt {{x^2} + 3\sqrt[3]{{{x^4}{y^2}}} + 3\sqrt[3]{{{x^2}{y^4}}} + {y^2}} \hfill \\ = \sqrt {{x^2} + 3\sqrt[3]{{{x^4}{y^2}}} + 3\sqrt[3]{{{x^2}{y^4}}} + {y^2}} + \sqrt {{x^2} + 3\sqrt[3]{{{x^4}{y^2}}} + 3\sqrt[3]{{{x^2}{y^4}}} + {y^2}} \hfill \\ > \sqrt {{x^2} + 3\sqrt[3]{{{x^4}{y^2}}}} + \sqrt {3\sqrt[3]{{{x^2}{y^4}}} + {y^2}} \hfill \\ > \sqrt {{x^2} + \sqrt[3]{{{x^4}{y^2}}}} + \sqrt {\sqrt[3]{{{x^2}{y^4}}} + {y^2}} = P \hfill \\ \Rightarrow P < Q \hfill \\ \end{matrix}

  • Câu 9: Thông hiểu

    Cho hàm số y = {x^{\frac{{ - 3}}{4}}}. Khẳng định nào sau đây sai?

    Hàm số y = {x^{\frac{{ - 3}}{4}}} có các tính chất như sau:

    Đồ thị hàm số nhận trục tung làm tiệm cận đứng

    Đồ thị hàm số nhận trục hoành làm tiệm cận ngang

    Là hàm số nghịch biến trên \left( {0; + \infty } ight)

  • Câu 10: Thông hiểu

    Hàm số nào sau đây nghịch biến trên tập xác định của nó?

    Ta có: y = {x^{ - \frac{5}{2}}} \Rightarrow y' = - \frac{5}{2}.{x^{ - \frac{7}{2}}};\forall x > 0 nên hàm số nghịch biến trên tập xác định của nó.

  • Câu 11: Vận dụng cao

    Tìm mệnh đề đúng trong các mệnh đề dưới đây:

    Giả sử M\left( {{x_0};{a^{{x_0}}}} ight) thuộc đồ thị hàm số y = {x^\alpha }

    Xét N\left( { - {x_0};{{\left( {\frac{1}{a}} ight)}^{ - {x_0}}}} ight) thuộc đồ thị hàm số y = {\left( {\frac{1}{a}} ight)^x}

    Rõ ràng {\left( {\frac{1}{a}} ight)^{ - {x_0}}} = {\left( { - {a^{ - 1}}} ight)^{ - {x_0}}} = {a^{{x_0}}}

    Khi đó N\left( { - {x_0};{a^{{x_0}}}} ight) và ta thấy rằng hai điểm M và N đối xứng với nhau qua trục Oy

    Do đó đồ thị hàm số y = {x^\alpha } và y = {\left( {\frac{1}{a}} ight)^x} đối xứng nhau qua trục Oy

  • Câu 12: Thông hiểu

    Tính đạo hàm của hàm số y = {\left( {{x^2} - 3x + 2} ight)^{\sqrt 3 }}

    Ta có:

    \begin{matrix} y' = \sqrt 3 .{\left( {{x^2} - 3x + 2} ight)^{\sqrt 3 - 1}}.\left( {{x^2} - 3x + 1} ight)\prime \hfill \\ \Rightarrow y' = \sqrt 3 .\left( {2x - 3} ight).{\left( {{x^2} - 3x + 2} ight)^{\sqrt 3 - 1}} \hfill \\ \end{matrix}

  • Câu 13: Thông hiểu

    Với a là một số thực dương thì biểu thức P = \frac{{{a^{\sqrt 7 + 1}}.{a^{2 - \sqrt 7 }}}}{{{{\left( {{a^{\sqrt 2 - 2}}} ight)}^{\sqrt 2 + 2}}}} được rút gọn là:

    Ta có: P = \frac{{{a^{\sqrt 7 + 1}}.{a^{2 - \sqrt 7 }}}}{{{{\left( {{a^{\sqrt 2 - 2}}} ight)}^{\sqrt 2 + 2}}}} = \frac{{{a^3}}}{{{a^{ - 2}}}} = {a^5}

  • Câu 14: Vận dụng

    Cho hình vẽ sau là đồ thị của ba hàm số y = {x^\alpha };y = {x^\beta };y = {x^\gamma } với x > 0 và \alpha ;\beta ;\gamma là các số thực cho trước, mệnh đề nào sau đây đúng?

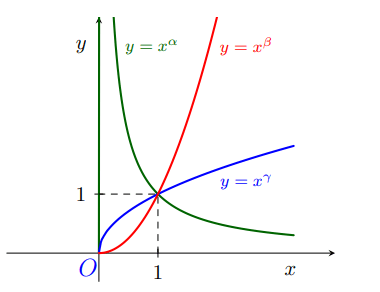
    Chọn mệnh đề đúng

    Hàm số {x^\alpha } nghịch biến trên \alpha < 0

    Các hàm số y = {x^\beta };y = {x^\gamma } đồng biến nên \beta ;\gamma > 0

    Tại x = 3 thì {3^\beta } > {3^\gamma } \Rightarrow \beta > \gamma

  • Câu 15: Thông hiểu

    Cho đồ thị hàm số y = {x^{ - \sqrt 2 }}. Khẳng định nào dưới đây đúng?

     Theo định nghĩa của hàm số lũy thừa, đồ thị hàm số có tiệm cận đứng là x = 0

    Ta có: \mathop {\lim }\limits_{x \to + \infty } y = 0 suy ra đồ thị hàm số có tiệm cận ngang là y = 0

    Vậy đồ thị hàm số có tiệm cận ngang là y = 0 và tiệm cận đứng là x = 0

  • Câu 16: Vận dụng

    Cho f\left( x ight) = \sqrt {1 + 3x} - \sqrt[3]{{1 + 2x}};g\left( x ight) = \sin x. Tính giá trị của biểu thức \frac{{f'\left( 0 ight)}}{{g'\left( 0 ight)}}

    Ta có: 

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {f'\left( x ight) = \dfrac{3}{{2\sqrt {1 + 3x} }} - \dfrac{2}{{3\sqrt[3]{{{{\left( {1 + 2x} ight)}^2}}}}} \Rightarrow f'\left( 0 ight) = \dfrac{5}{6}} \\ {g'\left( x ight) = \cos x \Rightarrow g'\left( 0 ight) = 1} \end{array}} ight. \hfill \\ \Rightarrow \frac{{f'\left( 0 ight)}}{{g'\left( 0 ight)}} = \dfrac{5}{6} \hfill \\ \end{matrix}

  • Câu 17: Nhận biết

    Đạo hàm của hàm số y = \frac{{{e^{4x}}}}{5}

    Ta có: y' = \frac{1}{5}\left( {{e^{4x}}} ight)' = \frac{1}{5}\left( {4x} ight)'.{e^{4x}} = \frac{4}{5}.{e^{4x}}

  • Câu 18: Nhận biết

    Cho hàm số y = {\left( {{x^2} - 2x + 1} ight)^{\frac{1}{3}}}. Tập xác định của hàm số đã cho là:

    Điều kiện xác đinh: {x^2} - 2x + 1 > 0 \Rightarrow x e 1

    => Tập xác định của hàm số là: D = \mathbb{R}\backslash \left\{ 1 ight\}

  • Câu 19: Vận dụng

    Cho biết {\left( {x - 2} ight)^{ - \frac{1}{3}}} > {\left( {x - 2} ight)^{ - \frac{1}{6}}}, khẳng định nào sau đây đúng?

    Điều kiện: x - 2 > 0 \to x > 2

    Ta có:

    - \frac{1}{3} > - \frac{1}{6} \Rightarrow {\left( {x - 2} ight)^{ - \frac{1}{3}}} > {\left( {x - 2} ight)^{ - \frac{1}{6}}}

    \Rightarrow x - 2 < 1 \Rightarrow x < 3

    Vậy 2 < x < 3

  • Câu 20: Thông hiểu

    Viết biểu thức \sqrt {a\sqrt {a\sqrt a } } :{a^{\frac{{11}}{6}}} với a > 0 dưới dạng lũy thừa với số mũ hữu tỉ?

    Ta có: 

    \begin{matrix} A = \sqrt {a\sqrt {a\sqrt a } } :{a^{\frac{{11}}{6}}} = {\left( {a\sqrt {{a^{\frac{3}{2}}}} } ight)^{\frac{1}{2}}}:{a^{\frac{{11}}{6}}} \hfill \\ = {\left( {a.{a^{\frac{3}{8}}}} ight)^{\frac{1}{2}}}:{a^{\frac{{11}}{6}}} = {\left( {{a^{\frac{7}{4}}}} ight)^{\frac{1}{2}}}:{a^{\frac{{11}}{6}}} = {a^{\frac{7}{8}}}:{a^{\frac{{11}}{6}}} = {a^{\frac{{23}}{{24}}}} \hfill \\ \end{matrix}

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Hàm số lũy thừa Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 20 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Hàm số lũy thừa
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập