Cho hai hình bình hành ![]() và
và ![]() nằm trong hai mặt phẳng phân biệt. Xét tính đúng sai của các mệnh đề sau:
nằm trong hai mặt phẳng phân biệt. Xét tính đúng sai của các mệnh đề sau:
a) ![]() . Sai||Đúng
. Sai||Đúng
b) ![]() . Đúng||Sai
. Đúng||Sai
c) ![]() . Sai||Đúng
. Sai||Đúng
d) Sáu điểm ![]() là 6 đỉnh của một hình lăng trụ tam giác. Đúng||Sai
là 6 đỉnh của một hình lăng trụ tam giác. Đúng||Sai
Cho hai hình bình hành và
nằm trong hai mặt phẳng phân biệt. Xét tính đúng sai của các mệnh đề sau:
a) . Sai||Đúng
b) . Đúng||Sai
c) . Sai||Đúng
d) Sáu điểm là 6 đỉnh của một hình lăng trụ tam giác. Đúng||Sai
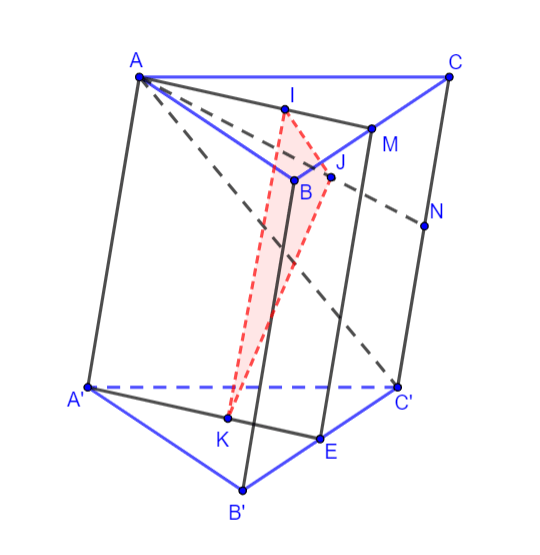
Hình vẽ minh họa
a) Sai: và
cắt nhau tại
.
b) Đúng.
Vì là hình bình hành nên
, suy ra
.
Vì là hình bình hành nên
, suy ra
.
Mà và
cắt nhau nên
.
c) Sai: Vì và
có điểm
chung.
d) Đúng:
Vì và
là hình bình hành nên
đôi một song song
Mặt khác (theo câu b)
Do đó 6 điểm là 6 đỉnh của một hình lăng trụ tam giác