Lớp 11 Toán 11 - Kết nối tri thức với cuộc sống

Đề kiểm tra 15 phút Toán 11 Chương 7 Kết nối tri thức

Mô tả thêm: Đề kiểm tra 15 phút Toán 11 Quan hệ vuông góc trong không gian gồm 20 câu hỏi trắc nghiệm giúp bạn học ôn tập, củng cố lại kiến thức sách Kết nối tri thức.
  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Cho khối lăng trụ đứng ABC.A'B'C', đáy ABC có AB = AC = a;\widehat{BAC} = 120^{0}. Tính thể tích của khối lăng trụ đã cho biết \left( (AB'C');(ABCD) ight) = 60^{0}.

    Hình vẽ minh họa

    Gọi H là trung điểm của B’C’, khi đó góc giữa mặt phẳng (AB’C’) và (ABCD) là góc \widehat{AHA'} = 60^{0}

    Ta có:

    S_{ABC} = \frac{1}{2}AC.AB.sin120^{0} = \frac{a^{2}\sqrt{3}}{4}

    B'C' = BC = \sqrt{AB^{2} + AC^{2} - 2AB.AC.cos120^{0}}

    = \sqrt{a^{2} + a^{2} - 2.a.a.\left( - \frac{1}{2} ight)} = a\sqrt{3}

    \Rightarrow AH' = \frac{2S_{ABC}}{B'C'} = \frac{a}{2}

    \Rightarrow AA' = A'H.tan60^{0} = \frac{a\sqrt{3}}{2}

    Vậy V = S_{ACB}.AA' = \frac{3a^{3}}{8}

  • Câu 2: Vận dụng

    Cho tứ diện ABCD có AB, BC, CD đôi một vuông góc với nhau và AB = a, BC = b, CD = c. Độ dài đoạn thẳng AD bằng bao nhiêu?

    Hình vẽ minh họa:

    Ta có: \left\{ \begin{matrix} BC\bot AB \\ CD\bot AB \\ \end{matrix} ight.\ \Rightarrow AB\bot(BCD)

    => Tam giác ABD vuông tại B.

    Ta có: \left\{ \begin{matrix} CD\bot AB \\ CD\bot BC \\ \end{matrix} ight.\ \Rightarrow CD\bot(ABC)

    => Tam giác BCD vuông tại C.

    Ta có: \left\{ \begin{matrix} AD^{2} = AB^{2} + BD^{2} \\ BD^{2} = BC^{2} + CD^{2} \\ \end{matrix} ight.

    \begin{matrix}\Rightarrow AD^{2} = AB^{2} + BC^{2} + CD^{2} \hfill \\\Rightarrow AD = \sqrt{AB^{2} + BC^{2} + CD^{2}} \hfill \\\Rightarrow AD = \sqrt{a^{2} + b^{2} + c^{2}} \hfill \\\end{matrix}

  • Câu 3: Thông hiểu

    Cho tứ diện ABCD với các đường thẳng AB, AC, AD đôi một vuông góc, H là trực tâm tam giác BCD. Góc giữa mặt phẳng (BCD) và mặt phẳng (ACD) bằng góc nào trong các góc sau đây?

    Dễ thấy rằng BA⊥(ACD), AH⊥(BCD), suy ra góc giữa mặt phẳng (BCD) và mặt phẳng (ACD) bằng góc giữa hai đường thẳng BA và AH, tức là bằng góc \widehat{BAH}

  • Câu 4: Nhận biết

    Cho hình lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác đều, M là trung điểm của BC. Khẳng định nào sau đây đúng?

    Hình vẽ minh họa

    Ta có tam giác ABC đều và M là trung điểm của BC nên AM\bot BC

    Ta có: \left\{ \begin{matrix} AM\bot BC \\ BC//B'C' \\ \end{matrix} ight.\ \Rightarrow AM\bot B'C'

  • Câu 5: Nhận biết

    Cho hình chóp S.ABC, tam giác ABC vuông tại B, cạnh bên SA vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SB (tham khảo hình vẽ bên). Mệnh đề nào sau đây sai?

    Ta có: SA ⊥ (ABC) => SA ⊥ BC

    Mặt khác BC ⊥ AB

    Suy ra BC ⊥ (SAB) nên hình chiếu vuông góc của SC trên (SAB) là SB

    Vậy \widehat{\left( SC,(SAB) ight)} =\widehat{(SC,SB)} = \widehat{BSC\ }(vì tam giác SBC vuông tại B)

  • Câu 6: Vận dụng cao

    Cho hình lập phương ABCD.A’B’C’D’ có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và điểm M thuộc đoạn OI sao cho MO = 2MI (tham khảo hình vẽ). Khi đó sin của góc tạo bởi hai mặt phẳng (MC’D’) và (MAB) bằng:

    Hình ảnh minh họa:

    Do AB // C’D’ nên giao tuyến của (MAB) và (MC’D’) là đường thẳng ∆ // AB // C’D’.

    Gọi P, Q lần lượt là trung điểm của D’C’ và AB ta có:

    \left\{ \begin{matrix} MP\bot C’D’ \\ MQ\bot AB \\ \end{matrix} ight.=> MP ⊥ ∆, MQ ⊥ ∆.

    Như vậy góc giữa (MAB) và (MC0’’) là góc giữa MP và MQ.

    Không mất tính tổng quát, ta cho cạnh hình lập phương là 6.

    Khi đó \left\{ \begin{matrix} MP = \sqrt{IM^{2} + IP^{2}} = \sqrt{10} \\ MQ = \sqrt{34};PQ = 6\sqrt{2} \\ \end{matrix} ight.

    Áp dụng định lí cosin cho tam giác MPQ ta được:

    \cos\widehat{PMQ} = \frac{MP^{2} + MQ^{2} - PQ^{2}}{2MP.MQ} = - \frac{14}{\sqrt{340}}

    Góc α là góc giữa hai mặt phẳng (MC’D’) và (MAB) ta có:

    \cos\alpha = \frac{14}{\sqrt{340}} = \frac{7\sqrt{85}}{85} \Rightarrow \sin\alpha = \frac{6\sqrt{85}}{85}

  • Câu 7: Nhận biết

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và AB = a, SA ⊥ (ABC), SA = a. Góc giữa đường thẳng SB và mặt phẳng đáy là:

    Hình vẽ minh họa:

    Theo bài ta có AB là hình chiếu của SB trên (ABC)

    Vậy \widehat{\left( SB,(ABC) ight)} =\widehat{(SB,\ AB)} = \widehat{SBA}

    Mà ∆SBA vuông cân tại A nên \widehat{SBA}= 45^{0}

  • Câu 8: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA\bot(ABCD). Biết diện tích tam giác SBD bằng a^{2}. Khi đó SA bằng:

    Hình vẽ minh họa

    Gọi O là tâm của đáy.

    Khi đó BD\bot(SAC) \Rightarrow BD\bot SO \Rightarrow S_{SBD} = \frac{1}{2}.SO.BD = a^{2}

    \Rightarrow SO = \frac{2a^{2}}{a\sqrt{2}} = a\sqrt{2}

    \Rightarrow SA = \sqrt{SO^{2} - AO^{2}} = \sqrt{2a^{2} - \frac{a^{2}}{2}} = \frac{a\sqrt{6}}{2}

  • Câu 9: Nhận biết

    Trong không gian cho ba đường thẳng phân biệt a, b, c. Khẳng định nào sau đây sai?

    Mệnh đề đúng: Nếu a và b cùng vuông góc với c thì a // b

  • Câu 10: Nhận biết

    Tính thể tích khối lập phương có cạnh bằng 3a?

    Ta có: V = (3a)^{3} = 27a^{3}

  • Câu 11: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ⊥ (ABCD). Gọi AM, AN lần lượt là đường cao của tam giác SAB và tam giác SAD. Khẳng định nào dưới đây là khẳng định đúng?

    Hình vẽ minh họa:

    Khẳng định đúng trong các khẳng định đã cho

    Ta có: SA ⊥ (ABCD) => SA ⊥ BC

    Mà AB ⊥ BC => BC ⊥ (SAB)

    => BC ⊥ AE

    Mà AM nằm trong mặt phẳng (SAB)

    Xét tam giác SAB có:

    AM ⊥ SB

    Mà BC ⊥ AM => AM ⊥ (SBC) => AM ⊥ SC

    Chứng minh tương tự ta được: AN ⊥ SC

    => SC ⊥ (AMN)

  • Câu 12: Nhận biết

    Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến ∆. Gọi ϕ là góc giữa (P) và (Q). Có tất cả bao nhiêu mệnh đề đúng trong các mệnh đề sau?

    (1) ϕ bằng góc giữa hai đường thẳng a và b cùng vuông góc với ∆.

    (2) ϕ bằng góc giữa hai đường thẳng a và b cùng vuông góc với ∆, lần lượt nằm trên (P) và (Q).

    (3) ϕ bằng góc giữa hai đường thẳng a và b đồng quy với ∆, cùng vuông góc với ∆, lần lượt nằm trên (P) và (Q).

    Ta có: a và b chỉ cần lần lượt nằm trong (P), (Q) cùng vuông góc với ∆ là đủ, thêm đồng quy với ∆ càng tốt nên có tất cả 2 mệnh đề đúng.

  • Câu 13: Vận dụng

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 10. Cạnh bện SA vuông góc với mặt phẳng (ABCD) và SC =10\sqrt{5}. Gọi M, N lần lượt là trung điểm của SA và CD. Tính khoảng cách d giữa BD và MN.

    Hình vẽ minh họa:

    Gọi P là trung điểm BC và E = NP ∩ AC

    => PN // BD => BD // (MNP)

    => d(BD, MN) = d(BD, (MNP)) = d(O, (MNP)) = \frac{1}{3}d(A, (MNP))

    Kẻ AK ⊥ ME

    Khi đó d(A, (MNP)) = AK.

    Ta tính được:

    \begin{matrix}SA = \sqrt{SC^{2} - AC^{2}} = 10\sqrt{3} \\\Rightarrow MA = 5\sqrt{3};AE = \dfrac{3}{4}AC = \dfrac{15\sqrt{2}}{2} \\\end{matrix}

    Xét tam giác vuông MAE ta có:

    AK = \frac{MA.AE}{\sqrt{MA^{2} +AE^{2}}} = 3\sqrt{5}

    \Rightarrow d(BD;MN) = \frac{1}{3}AK =\sqrt{5}

  • Câu 14: Nhận biết

    Tính thể tích khối lập phương có cạnh bằng 2a?

    Ta có: V = (2a)^{3} = 8a^{3}

  • Câu 15: Thông hiểu

    Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a; SA = a;SA\bot(ABCD). Khoảng cách giữa hai đường thẳng SC;BD bằng bao nhiêu?

    Hình vẽ minh họa

    Dựng Cx//BD;(\alpha) = (SC;Cx)

    \Rightarrow d(BD;SC) = d\left( BD;(\alpha) ight)

    d\left( BD;(\alpha) ight) = d\left( O;(\alpha) ight) = \frac{1}{2}d\left( A;(\alpha) ight)

    Dựng AK\bot SC. Dễ thấy AK\bot(\alpha) \Rightarrow d\left( A;(\alpha) ight) = AK

    \frac{1}{AK^{2}} = \frac{1}{SA^{2}} + \frac{1}{AC^{2}} \Rightarrow AK = \frac{a\sqrt{6}}{3}

    \Rightarrow d\left( O;(\alpha) ight) = \frac{a\sqrt{6}}{3}

  • Câu 16: Nhận biết

    Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Dựng mặt phẳng (P) cách đều năm điểm A, B, C, D và S. Hỏi có tất cả bao nhiêu mặt phẳng (P) như vậy?

    Gọi O là tâm hình bình hành ABCD.

    Các mặt phẳng cách đều A, B, C, D và S là

    1) Mặt phẳng qua trung điểm của SA, SB, SC, SD

    2) Mặt phẳng qua O và song song (SAB)

    3) Mặt phẳng qua O và song song (SAD)

    4) Mặt phẳng qua O và song song (SCD)

    5) Mặt phẳng qua O và song song (SBC)

  • Câu 17: Thông hiểu

    Cho hình chóp S.ABC có SA = SB và CA = CB. Tính số đo góc giữa hai đường thẳng chéo nhau SC và AB.

    Hình vẽ minh họa:

    Số đo góc giữa hai đường thẳng chéo nhau

    \begin{matrix} \overrightarrow {SC} \overrightarrow {AB} = - \overrightarrow {CS} .(\overrightarrow {CB} - \overrightarrow {CA} ) \hfill \\ = \overrightarrow {CS} .\overrightarrow {CA} - \overrightarrow {CS} .\overrightarrow {CB} \hfill \\ = CS.CA.\cos \widehat {SCA} - CS.CB.\cos \widehat {SCB} \hfill \\ = CS.CA.\dfrac{{S{C^2} + C{A^2} - S{A^2}}}{{2SC.CA}} \hfill \\ - CS.CB.\dfrac{{S{C^2} + C{B^2} - S{B^2}}}{{2SC.CB}} \hfill \\ = \frac{{S{C^2} + C{A^2} - S{A^2}}}{2} - \dfrac{{S{C^2} + C{B^2} - S{B^2}}}{2} = 0 \hfill \\ ({\text{Do }}SA = SB{\text{ v\`a }}CA = CB) \Rightarrow SC \bot AB \hfill \\ \end{matrix}

  • Câu 18: Vận dụng

    Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc với nhau. Tính sin góc giữa đường thẳng SC và mặt phẳng (SAD).

    Tính sin góc giữa đường thẳng SC và mặt phẳng (SAD)

    Gọi I là trung điểm của AB. Khi đó SI \bot \left( {ABCD} ight)

    Ta có \left\{ \begin{gathered} AD \bot AB \hfill \\ AD \bot SI \hfill \\ \end{gathered} ight. \Rightarrow AD \bot \left( {SAB} ight) mà AD \subset \left( {SAD} ight) \Rightarrow \left( {SAD} ight) \bot \left( {SAB} ight)

    Dựng BH \bot SA tại H suy ra SH \bot \left( {SAD} ight)

    Trong mặt phẳng (SAD) kẻ Hx // AD. Trong mặt phẳng (BC, Hx) qua C kẻ đường thẳng song song với BH cắt Hx tại K thì CK \bot \left( {SAD} ight)

    Suy ra SK là hình chiếu vuông góc của SC trên mặt phẳng (SAD) nên góc giữa đường thẳng SC và mặt phẳng (SAD) là góc \widehat {CSK}

    Ta có BH = CK = \frac{{a\sqrt 3 }}{2}

    Trong tam giác SCI có

    SC = \sqrt {S{I^2} + I{C^2}} = \sqrt {\frac{{3{a^2}}}{4} + \frac{{5{a^2}}}{4}} = a\sqrt 2

    Suy ra \sin \widehat {CSK} = \frac{{CK}}{{SC}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{{a\sqrt 2 }} = \frac{{\sqrt 6 }}{4}

  • Câu 19: Thông hiểu

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy. Gọi H, K lần lượt là hình chiếu vuông góc của A trên các cạnh SB, SC. Giả sử HK cắt BC tại D. Khi đó:

    a) \widehat{(AC;AD)} = 90^{0} Đúng||Sai

    b) AH\bot(SBC) Đúng||Sai

    c) \widehat{(SC;HK)} = 90^{0} Đúng||Sai

    d) Tam giác SBC cân tại B. Sai||Đúng

    Đáp án là:

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy. Gọi H, K lần lượt là hình chiếu vuông góc của A trên các cạnh SB, SC. Giả sử HK cắt BC tại D. Khi đó:

    a) \widehat{(AC;AD)} = 90^{0} Đúng||Sai

    b) AH\bot(SBC) Đúng||Sai

    c) \widehat{(SC;HK)} = 90^{0} Đúng||Sai

    d) Tam giác SBC cân tại B. Sai||Đúng

    \widehat{(AC;AD)} = 90^{0} đúng

    AH\bot(SBC) đúng

    \widehat{(SC;HK)} = 90^{0} đúng

    Tam giác SBC cân tại B. sai

  • Câu 20: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , SA vuông góc với mặt phẳng (ABCD), AB = BC = a, AD = 2a. Biết góc giữa SC và mặt phẳng (ABCD) bằng 450. Tính góc giữa mặt phẳng (SAD) và (SCD).

    Tính góc giữa mặt phẳng (SAD) và (SCD)

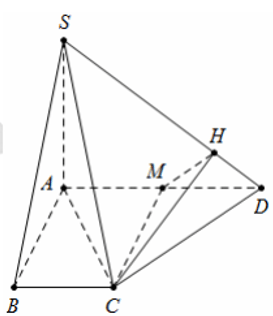
    Tam giác ABC vuông cân tại B, suy ra AC = AB\sqrt 2 = a\sqrt 2

    Vì SA \bot \left( {ABCD} ight) nên AC là hình chiếu của SC trên mặt phẳng (ABCD).

    Khi đó

    \begin{matrix} \widehat {\left( {SC;\left( {ABCD} ight)} ight)} = \widehat {\left( {SC;AC} ight)} = \widehat {SCA} = {45^0} \hfill \\ \Rightarrow SA = AC = a\sqrt 2 \hfill \\ \end{matrix}

    Gọi M là trung điểm của AD => CM ⊥ AD.

    Mà CM ⊥ SA nên CM ⊥ (SAD) => CM ⊥ SD

    Hạ CH ⊥ SD . Khi đó SD ⊥ (CMH) => MH ⊥ SD

    Ta có:

    \begin{matrix} \left\{ {\begin{array}{*{20}{l}} {(SAD) \cap (SCD) = SD} \\ {MH \subset (SAD)} \\ {MH \bot SD} \\ {CH \subset (SCD)} \\ {CH \bot SD} \end{array}} ight. \hfill \\ \Rightarrow \widehat {((SAD),(SCD))} = \widehat {(MH,CH)} = \widehat {MHC} \hfill \\ \end{matrix}

    Ta lại có: SD = \sqrt {S{A^2} + A{D^2}} = a\sqrt 6 ;CM = AB = a

    \begin{matrix} \Delta SAD \sim \Delta MHD \hfill \\ \Rightarrow \dfrac{{SA}}{{SD}} = \dfrac{{MH}}{{MD}} \hfill \\ \Rightarrow MH = \dfrac{{SA.MD}}{{SD}} = \dfrac{{a\sqrt 2 a}}{{a\sqrt 6 }} = \dfrac{{a\sqrt 3 }}{3} \hfill \\ \end{matrix}

    Tam giác MHC vuông tại M

    \Rightarrow \tan \widehat {MHC} = \frac{{CM}}{{MH}} = \frac{a}{{\frac{{a\sqrt 3 }}{3}}} = \sqrt 3 \Rightarrow \widehat {MHC} = {60^0}

    Vậy \left( {\widehat {\left( {SAD} ight);\left( {SCD} ight)}} ight) = {60^0}

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Toán 11 Chương 7 Kết nối tri thức Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 68 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Toán 11 Chương 7 Kết nối tri thức
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập