Lớp 11 Toán 11 - Cánh Diều

Đề kiểm tra 15 phút Toán 11 Chương 8 Cánh Diều

Cùng nhau thử sức với bài kiểm tra 15 phút Toán 11 Cánh Diều Chương 8: Quan hệ vuông góc trong không gian. Phép chiếu vuông góc nha!

  • Thời gian làm: 15 phút
  • Số câu hỏi: 20 câu
  • Số điểm tối đa: 20 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Nhận biết

    Cho hình chóp ABCD có đáy ABCD là hình thoi tâm O, cạnh bên SO vuông góc với mặt phẳng đáy. Gọi \alpha là góc giữa đường thẳng SD với mặt phẳng đáy. Khi đó:

    Hình vẽ minh họa

    Ta có: SO\bot(ABCD) suy ra OD là hình chiếu vuông góc của SD lên mặt phẳng (ABCD)

    Suy ra \widehat{\left( SD;(ABCD) ight)} = \widehat{(SD;SO)} = \widehat{SDO}

    Vậy \alpha = \widehat{SDO}

  • Câu 2: Vận dụng

    Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = 2a, BC = a. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AB, góc giữa đường thẳng SC và mặt phẳng đáy bằng 600. Tính cosin góc giữa hai đường thẳng SB và AC.

    Tính cosin góc giữa hai đường thẳng SB và AC

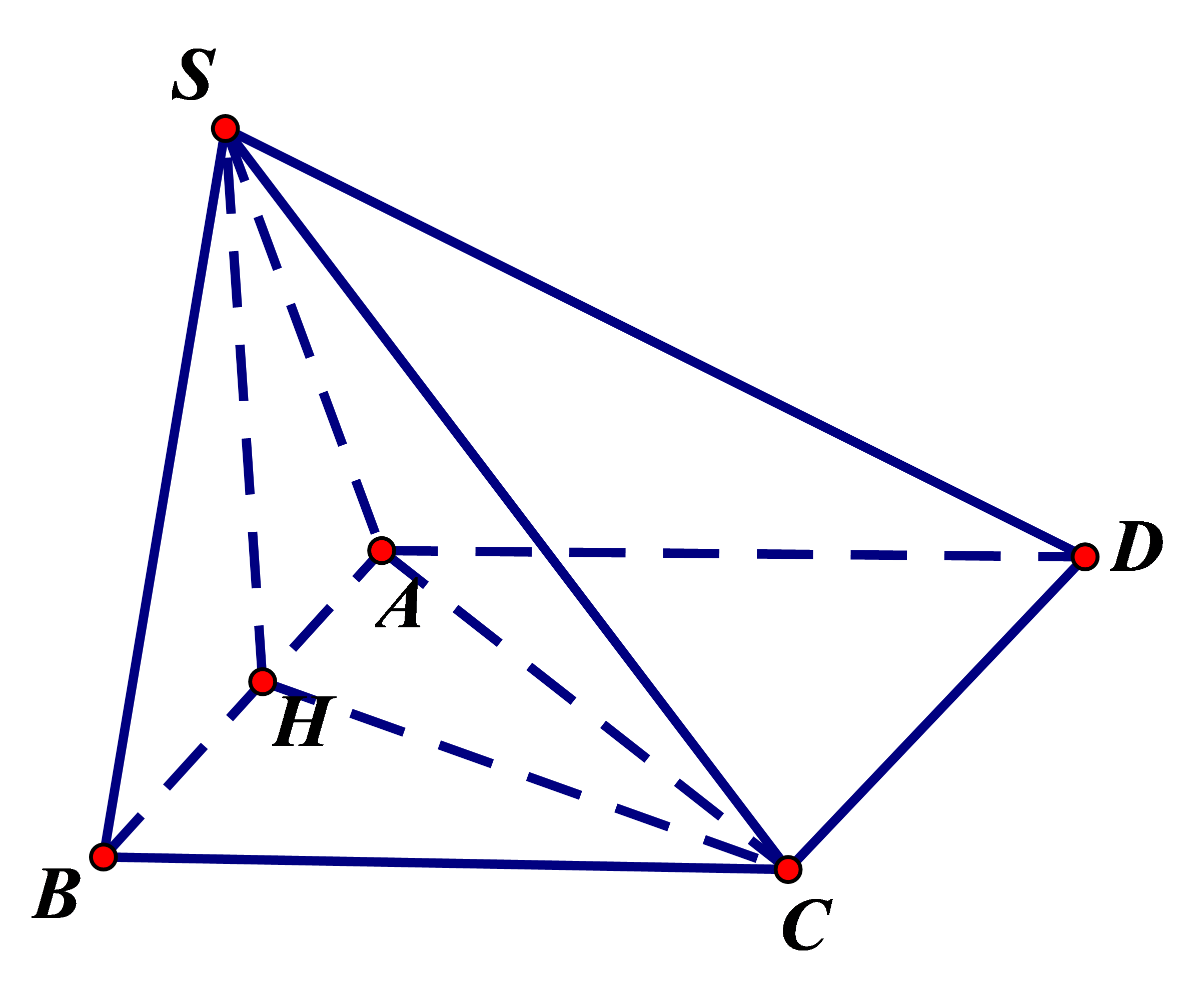
    +) Ta có:

    \begin{matrix} \overrightarrow {SB} .\overrightarrow {AC} = \left( {\overrightarrow {SH} + \overrightarrow {HB} } ight)\left( {\overrightarrow {AB} + \overrightarrow {BC} } ight) \hfill \\ = \overrightarrow {SH} .\overrightarrow {AB} + \overrightarrow {SH} .\overrightarrow {BC} + \overrightarrow {HB} .\overrightarrow {AB} + \overrightarrow {HB} .\overrightarrow {BC} \hfill \\ = \overrightarrow {HB} .\overrightarrow {AB} + \overrightarrow {HB} .\overrightarrow {BC} \hfill \\ = \dfrac{1}{2}A{B^2} = 2{a^2} \hfill \\ \end{matrix}

    +) Mặt khác

    \begin{matrix} AC = a\sqrt 5 ;CH = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \hfill \\ SH = CH.\tan \widehat {SCH} = a\sqrt 6 \hfill \\ SB = \sqrt {S{H^2} + H{B^2}} = \sqrt {{{\left( {a\sqrt 6 } ight)}^2} + {a^2}} = a\sqrt 7 \hfill \\ \end{matrix}

    => \cos \left( {SB,AC} ight) = \frac{{\left| {\overrightarrow {SB} .\overrightarrow {AC} } ight|}}{{SB.AC}} = \frac{{2{a^2}}}{{a\sqrt 7 .a\sqrt 5 }} = \frac{2}{{\sqrt {35} }}

  • Câu 3: Vận dụng

    Cho hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng x và \widehat{BAD} = \widehat{DAA'} = \widehat{A'AB} = 60^{0}. Gọi M,N lần lượt là trung điểm câc các cạnh AA';CD. Tính cosin góc giữa hai đường thẳng MN và B'C?

    Hình vẽ minh họa

    Gọi P là trung điểm của DC’. Ta có: \left\{ \begin{matrix} A'D//B'C \\ MN//A'P \\ \end{matrix} ight.

    Suy ra (MN,B'C) = (A'P,A'D) = \widehat{DA'P}

    Xét tam giác ADA’ có \left\{ \begin{matrix} AD = AA' \\ \widehat{DAA'} = 60^{0} \\ \end{matrix} ight. suy ra tam giác ADA’ là tam giác đều \Rightarrow A'D = x

    Xét tam giác A’AB có \left\{ \begin{matrix} AB = AA' \\ \widehat{A'AB} = 60^{0} \\ \end{matrix} ight. suy ra tam giác A’AB đều

    Do đó tam giác DD’C đều

    Vậy DC' = 2DP = 2.\frac{x\sqrt{3}}{2}= x\sqrt{3}

    Xét tam giác BAD có AD = AB và \widehat{BAD} = 60^{0} nên tam giác BAD là tam giác đều.

    Vì tam giác BAD đều nên tam giác B’A’D’ cùng là tam giác đều.

    Gọi A’I là đường cao của tam giác B’A’D’

    Khi đó: A'C' = 2A'I =2.\frac{x\sqrt{2}}{2} = x\sqrt{3}

    Dễ thấy A’P là đường trung tuyến của tam giác DA’C’ nên A'P = \sqrt{\frac{A'D'^{2} +A'C'^{2}}{2} - \frac{DC'^{2}}{4}} =\frac{x\sqrt{5}}{2}

    Áp dụng định lí cosin cho tam giác A’DP có:

    \Rightarrow \cos\widehat{DA'P} =\frac{A'D^{2} + A'P^{2} - DP^{2}}{2.A'D.A'P} =\frac{x\sqrt{5}}{10}

    \Rightarrow \cos(MN,B'C) = \left| \cos\widehat{DA'P} ight| = \frac{3\sqrt{5}}{10}

  • Câu 4: Nhận biết

    Cho khối chóp và lăng trụ có diện tích đáy, chiều cao tương ứng với nhau và thể tích lần lượt là V và V' . Khi đó tỉ số \frac{V}{V'} = 1/3

    (Kết quả ghi dưới dạng phân số tối giản a/b)

    Đáp án là:

    Cho khối chóp và lăng trụ có diện tích đáy, chiều cao tương ứng với nhau và thể tích lần lượt là V và V' . Khi đó tỉ số \frac{V}{V'} = 1/3

    (Kết quả ghi dưới dạng phân số tối giản a/b)

    Ta có:

    Thể tích khối chóp là: V = \frac{1}{3}B.h

    Thể tích hình lăng trụ là: V' = B.h

    Khi đó: \dfrac{V}{V'} =\dfrac{\dfrac{1}{3}B.h}{B.h} = \dfrac{1}{3}

  • Câu 5: Vận dụng

    Cho lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh đều bằng a. Khoảng cách giữa hai đường thẳng BC và AB’ bằng:

    Hình vẽ minh họa:

    Ta có BC // B’C’ => BC // (AB’C’)

    => d(BC, AB’) = d(BC, (AB’C’)) = d(B, (AB’C’)) = d(A’ ,(AB’C’))

    Gọi I và H lần lượt là hình chiếu vuông góc của A’ trên B’C’ và AI

    Ta có: B’C’⊥ A’I và B’C’⊥ A’A nên B’C’⊥ (A’AI) => B’C’⊥ A’H

    Mà AI ⊥ A’H

    => (AB’C’) ⊥ A’H.

    Khi đó:

    d\left( A';(AB'C') ight) =A'H = \frac{AA'.A'I}{\sqrt{AA'^{2} +A'I^{2}}}

    =\dfrac{a.\dfrac{a\sqrt{3}}{2}}{\sqrt{a^{2} + \left( \dfrac{a\sqrt{3}}{2}ight)^{2}}} = \dfrac{a\sqrt{21}}{7}

    Vậy khoảng cách cần tìm là \frac{a\sqrt{21}}{7}

  • Câu 6: Nhận biết

    Trong không gian cho đường thẳng a và điểm M. Có bao nhiêu đường thẳng đi qua M, cắt a và vuông góc với a?

    Có 1 nếu M không thuộc a, có vô số nếu M thuộc a

  • Câu 7: Thông hiểu

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, các cạnh AB = AC = a, các góc \widehat{SBA} = \widehat{SCA} = 90^{0}. Gọi H là hình chiếu vuông góc của S trên (ABC) và SH = a\sqrt{2}. Tính cosin góc giữa hai mặt phẳng (SAB) và (SAC).

    Đáp án: 1/3 (Ghi đáp án dưới dạng phân số tối giản a/b).

    Đáp án là:

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, các cạnh AB = AC = a, các góc \widehat{SBA} = \widehat{SCA} = 90^{0}. Gọi H là hình chiếu vuông góc của S trên (ABC) và SH = a\sqrt{2}. Tính cosin góc giữa hai mặt phẳng (SAB) và (SAC).

    Đáp án: 1/3 (Ghi đáp án dưới dạng phân số tối giản a/b).

    Hình vẽ minh họa

    Gọi (\alpha) là mặt phẳng qua B và vuông góc với AB \Rightarrow (\alpha) \cap (ABC) = Bt//AC.

    Gọi (\beta) là mặt phẳng qua C và vuông góc với AC

    \Rightarrow (\beta) \cap (ABC) =Ct'//AB

    Khi đó, (\alpha) \cap (\beta) = SH với H = Bt \cap Ct' là đỉnh thứ tư của hình vuông ABHC.

    Khi đó: \Delta SAB,\ \ \Delta SAC là hai tam giác vuông bằng nhau có SB = SC = a\sqrt{3},SA = 2a.

    Gọi I là chân đường cao hạ từ đỉnh B của tam giác SAB, ta có BI\bot SA,CI\bot SA.

    Vậy góc giữa hai mặt phẳng (SAB) và (SAC) là (IB;IC).

    Xét \Delta IBC cân tại I có IB = IC = \frac{a\sqrt{3}.a}{2a} = \frac{a\sqrt{3}}{2},BC = a\sqrt{2}.

    Ta có: \cos\widehat{BIC} = \frac{IB^{2} +IC^{2} - BC^{2}}{2IB.IC}= \dfrac{\dfrac{3a^{2}}{4} + \dfrac{3a^{2}}{4} -2a^{2}}{2.\dfrac{3a^{2}}{4}} = - \dfrac{1}{3}.

    Vậy cosin góc giữa hai mặt phẳng (SAB) và (SAC) bằng \frac{1}{3}.

  • Câu 8: Nhận biết

    Cho hình lập phương ABCD.A1B1C1D1. Chọn khẳng định sai?

    Hình vẽ minh họa:

    Dễ thấy

    Góc giữa B1D1 và AC bằng 900

    Góc giữa AD và C1B bằng 450

    Góc giữa BD và CA1 bằng 900

    Đều là các đáp án đúng

    Góc giữa B1D1 và AA1 bằng 600 sai vì \widehat{\left( B_{1}D_{1};AA_{1} ight)} = 90^{0}

  • Câu 9: Thông hiểu

    Đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ là tam giác đều cạnh bằng 4. Tính khoảng cách giữa hai đường thẳng AA’ và BC.

    Hình vẽ minh họa:

    Gọi M là trung điểm của BC. Khi đó AM ⊥ AA’ tại A, AM ⊥ BC tại M.

    Do đó, AM là đoạn vuông góc chung của AA’ và BC.

    => d(AA’, BC) = \frac{4\sqrt{3}}{2} = 2\sqrt{3}

  • Câu 10: Thông hiểu

    Cho hình chóp S.ABC có đáy ABC là hình tam giác vuông tại B, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi H;K lần lượt là hình chiếu của điểm A trên cạnh SB;SC. Kết luận nào sau đây sai?

    Hình vẽ minh họa

    Ta có: \left\{ \begin{matrix}SA\bot(ABC) \\BC \subset (ABC) \\\end{matrix} ight.\ \Rightarrow SA\bot BC;AB\bot BC

    \Rightarrow BC\bot(SAB) đúng

    Ta có: \left\{ \begin{matrix}BC\bot AH \\SC\bot AH \\\end{matrix} ight.\ \Rightarrow AH\bot(SBC) đúng

    Ta có: \left\{ \begin{matrix}AH\bot SC \\AK\bot SC \\\end{matrix} ight.\ \Rightarrow SC\bot(AHK) đúng

    Vậy kết luận sai là: AK\bot(SBC).

  • Câu 11: Thông hiểu

    Cho ba vecto \vec{n}, \vec{a}, \vec{b} bất kì đều khác với vecto \vec{0}. Nếu vecto \vec{n} vuông góc với cả hai vecto \vec{a} và \vec{b} thì \vec{n}, \vec{a} và \vec{b}:

    Nếu vecto \vec{n} vuông góc với cả hai vecto \vec{a} và \vec{b} thì \vec{n}, \vec{a} và \vec{b} thì có thể đồng phẳng.

  • Câu 12: Thông hiểu

    Cho hình chóp tam giác S.ABC có SA\bot(ABC);SA = a\sqrt{2}. Biết rằng tam giác ABC vuông cân tại B và AC = 2a. Tính góc giữa SB và (ABC)?

    Hình vẽ minh họa

    Ta có: SB \cap (ABC);SA\bot(ABC)

    => Hình chiếu vuông góc của SB trên mặt phẳng (ABC) là AB.

    => Góc giữa đường thẳng SB và mặt phẳng (ABC) là \widehat{SBA}

    Do tam giác ABC vuông cân tại B và AC = 2a nên AB = \frac{AC}{\sqrt{2}} = a\sqrt{2} = SA

    Suy ra tam giác SAB vuông cân tại A.

    Do đó \widehat{SBA} = 45^{0}

    Vậy góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 450.

  • Câu 13: Thông hiểu

    Cho khối hộp chữ nhật ABCD.A'B'C'D' có đáy là hình vuông, đường chéo BD = 2a. Biết góc giữa hai mặt phẳng (A'BD) và mặt phẳng (ABCD) bằng 60^{0}. Khi đó thể tích hình hộp chữ nhật bằng bao nhiêu?

    Hình vẽ minh họa

    Gọi góc giữa mặt phẳng (A'BD) và mặt phẳng (ABCD)là \alphavà O = AC \cap BD

    Ta có: \left\{ \begin{matrix} AO\bot BD \\ AA'\bot BD \\ \end{matrix} ight.\ \Rightarrow A'O\bot BD

    \Rightarrow \alpha = (AO;A'O) = \widehat{AOA'} = 60^{0}

    Ta có ABCD là hình vuông, BD = 2a nên AB = AD = a\sqrt{2}

    Ta có: AO = \frac{1}{2}AC = \frac{1}{2}BD = a

    Xét tam giác AOA’ có AA' = AO.tan60^{0} = a\sqrt{3}

    \Rightarrow V_{ABCD.A'B'C'D'} = AA'.S_{ABCD} = a\sqrt{3}.2a^{2} = 2a^{3}\sqrt{3}

  • Câu 14: Nhận biết

    Cho hình chóp S.ABCD có đáy là hình vuông ABCD, SA vuông góc với đáy. Kẻ AH vuông góc với SB (H ∈ SB). Chọn mệnh đề đúng.

    Hình vẽ minh họa:

    Ta có:

    SA ⊥ BC

    AB ⊥ BC

    => BC ⊥ (SAB) => BC ⊥ AH

    Mà AH ⊥ SB nên AH ⊥ (SBC) => AH ⊥ SC

  • Câu 15: Vận dụng

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, góc ABC bằng 600, tam giác SBC là tam giác đều có cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Tính số đo góc giữa đường thẳng SA và mặt phẳng đáy (ABC).

    Hình vẽ minh họa:

    Gọi H là trung điểm của BC => SH ⊥ (ABC)

    Vì SH ⊥ (ABC) => HA là hình chiếu vuông góc của SA trên mặt phẳng (SAB)

    => \left( SA,(ABC) ight) = (SA,AH) = \widehat{SAH}

    Xét tam giác SBC đều cạnh 2a => SH = a\sqrt{3}

    Tam giác ABC vuông tại A => AH = \frac{BC}{2} = a

    Tam giác SAH vuông nên

    \begin{matrix}\tan\widehat{SAH} = \dfrac{SH}{AH} = \sqrt{3} \hfill\\\Rightarrow \widehat{SAH} = 60^{0} \hfill \\\end{matrix}

  • Câu 16: Vận dụng cao

    Cho tứ diện ABCD có BD vuông góc với AB và CD. Gọi P và Q lần lượt là trung điểm của các cạnh CD và AB thỏa mãn BD : CD : PQ : AB = 3 : 4 : 5 : 6. Gọi ψ là góc giữa hai đường thẳng AB và CD. Tính giá trị của cosψ

    Hình vẽ minh họa:

    Do AB vuông góc với BD nên AB nằm trong mặt phẳng (α) chứa AB và vuông góc với BD. Dựng hình chữ nhật BDPR thì góc giữa hai đường thẳng AB và CD cũng là góc giữa hai đường thẳng AB và BR. Ta có:

    \cos\psi = \frac{\left| BQ^{2} + BR^{2}- QR^{2} ight|}{2BQ.BR} = \frac{|9 + 4 - 16|}{2.3.2} =\frac{1}{4}

  • Câu 17: Nhận biết

    Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OB = OC = a. Tính khoảng cách giữa hai đường thẳng OA và BC.

    Hình vẽ minh họa:

    Gọi M là trung điểm CB, ta có: OM ⊥ BC.

    Mặt khác vì OA, OB, OC đôi một vuông góc nên OA ⊥ (OBC)

    => OA ⊥ OM. Do đó khoảng cách giữa OA và BC là OM.

    Ta có: OM = \frac{1}{2}BC = \frac{a\sqrt{2}}{2}

  • Câu 18: Vận dụng

    Cho tứ diện ABCD có các cạnh AB,AC,AD đôi một vuông góc với nhau; AB = 8a;AC = 5a;AD = 6a. Gọi trung điểm của các cạnh BC,CD,DB lần lượt là J;Q;K. Tính thể tích tứ diện AJQK?

    Hình vẽ minh họa

    Ta có: V_{ABCD} = \frac{1}{2}AB.\frac{1}{2}AD.AC = 60a^{3}

    Nhận thấy S_{JQK} = \frac{1}{2}S_{JQKD} = \frac{1}{4}S_{BCD}

    V_{JQK} = \frac{1}{4}.V_{ABCD} = 15a^{3}

  • Câu 19: Thông hiểu

    Cho tứ diện đều ABCD có I và J lần lượt là trung điểm của AB và CD. Tính cosin góc giữa hai cạnh AJ và CI?

    Hình vẽ minh họa:

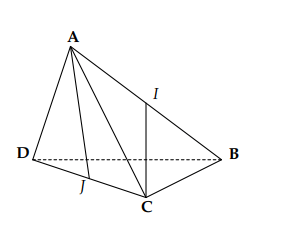
    Tính cosin góc giữa hai cạnh AJ và CI?

    Giả sử cạnh tứ diện đều bằng a. Khi đó:

    Ta có:

    \begin{matrix} \overrightarrow {AJ} = \dfrac{1}{2}\overrightarrow {AD} + \dfrac{1}{2}\overrightarrow {AC} \hfill \\ \overrightarrow {CI} = \overrightarrow {AI} - \overrightarrow {AC} = \dfrac{1}{2}\overrightarrow {AB} - \overrightarrow {AC} \hfill \\ \Rightarrow \overrightarrow {CI} .\overrightarrow {AJ} = \dfrac{1}{4}\left( {\overrightarrow {AB} - 2\overrightarrow {AC} } ight).\left( {\overrightarrow {AC} + \overrightarrow {AD} } ight) \hfill \\ \Rightarrow \overrightarrow {CI} .\overrightarrow {AJ} = - \dfrac{{{a^2}}}{2} \hfill \\ \Rightarrow \overrightarrow {CI} = \overrightarrow {AJ} = \dfrac{{a\sqrt 3 }}{2} \hfill \\ \Rightarrow \cos \left( {\overrightarrow {CI} ;\overrightarrow {AJ} } ight) = \dfrac{2}{3} \hfill \\ \end{matrix}

    Vậy cosin góc giữa hai cạnh AJ và CI bằng \frac{2}{3}

  • Câu 20: Thông hiểu

    Khối chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA = SB = 2a. Mặt phẳng (SAB) tạo với mặt phẳng đáy một góc 90^{0}. Xác định thể tích khối chóp S.ABCD?

    Hình vẽ minh họa

    Gọi H là trung điểm của AB

    Tam giác SAB cân tại S nên SH\bot AB

    Ta có: \left\{ \begin{matrix} SH\bot AB \\ (SAB)\bot(ABCD) \\ SH \subset (SAB) \\ AB = (SAB) \cap (ABCD) \\ \end{matrix} ight.\ \Rightarrow SH\bot(ABCD)

    Vậy SH là đường cao của hình chóp

    Xét tam giác AHS vuông tại H ta có:

    SH = \sqrt{SA^{2} - AH^{2}} = \sqrt{(2a)^{2} - \left( \frac{a}{2} ight)^{2}} = \frac{a\sqrt{15}}{2}

    Vậy thể tích hình chóp là:

    V = \frac{1}{3}.SH.S_{ABCD} = \frac{1}{3}.\frac{a^{2}\sqrt{15}}{2}.a^{2} = \frac{a^{3}\sqrt{15}}{6}

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 15 phút Toán 11 Chương 8 Cánh Diều Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 37 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 15 phút Toán 11 Chương 8 Cánh Diều
Thời gian còn lại 15:00 Số câu đã làm 0/20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập