Lớp 12 Toán 12

Đề kiểm tra 45 phút Chương 1 Khối đa diện

Hãy cùng thử sức kiểm tra đánh giá các kiến thức tổng quan với bài kiểm tra phút Chương 1: Khối đa diện Toán 12 các em nhé!

  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Vận dụng cao

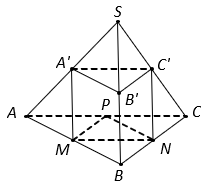
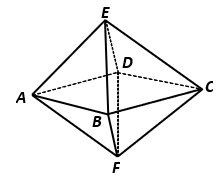
    Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề nào dưới đây đúng?

     

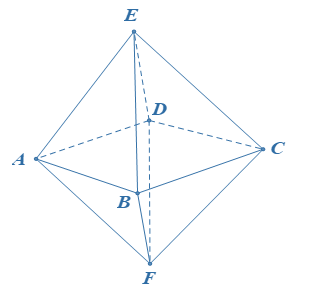
    Hình bát diện đều là hình có tám mặt bằng nhau và mỗi mặt là một tam giác đều. Gọi S_0 là diện tích tam giác đều cạnh a \xrightarrow{{}}\,{S_0} = \frac{{{a^2}\sqrt 3 }}{4}

    Vậy diện tích S cần tính là: S = 8.{S_0} = 8.\frac{{{a^2}\sqrt 3 }}{4} = 2\sqrt 3 \,{a^2}.

  • Câu 2: Vận dụng cao

    Cho tứ diện có thể tích bằng V. Gọi V' là thể tích của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính tỉ số \frac{{V'}}{V}.

     

    Xét khối  tứ diện và các điểm được kí hiệu như hình vẽ trên, ta có:

    \frac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \frac{{SA'}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}} = \frac{1}{8} \Rightarrow {V_{S.A'B'C'}} = \frac{V}{8}

    Tương tự \,{V_{A.A'MP}} = {V_{B.B'MN}} = {V_{C.C'NP}} = \frac{V}{8}.

    Do đó \,\,V' = {V_{S.ABC}} - \left( {{V_{S.A'B'C'}} + {V_{A.A'MP}} + {V_{B.B'MN}} + {V_{C.C'NP}}} ight)

    = \,\,V - \left( {\frac{V}{8} + \frac{V}{8} + \frac{V}{8} + \frac{V}{8}} ight) = \frac{V}{2}\,\, \Rightarrow \,\,\frac{{V'}}{V} = \frac{1}{2}.

  • Câu 3: Thông hiểu

    Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B và BA=BC=1. Cạnh A'B tạo với mặt đáy (ABC) góc 60^0. Tính thể tích V của khối lăng trụ đã cho.

     

    Vì ABC.A'B'C' là lăng trụ đứng nên AA' \bot \left( {ABC} ight), suy ra hình chiếu vuông góc của A'B trên mặt đáy (ABC) là AB.

    Do đó {60^0} = \widehat {A'B,\left( {ABC} ight)} = \widehat {A'B,AB} = \widehat {A'BA}.

    Tam giác vuông A'AB, ta có AA' = AB.\tan \widehat {A'BA} = \sqrt 3

    Diện tích tam giác là {S_{\Delta ABC}} = \frac{1}{2}BA.BC = \frac{1}{2}

    Vậy V = {S_{\Delta ABC}}.AA' = \frac{{\sqrt 3 }}{2}.

  • Câu 4: Thông hiểu

    Một hình đa diện có các mặt là những tam giác. Gọi M là tổng số mặt và C là tổng số cạnh của đa diện đó. Mệnh đề nào sau đây đúng.

     Vì mỗi mặt là những tam giác nên có tổng số cạnh là 3M.  Mỗi cạnh là cạnh chung của đúng hai mặt nên ta có hệ thức 3M = 2C.

  • Câu 5: Thông hiểu

    Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và khoảng cách từ A đến mặt phẳng (SBC) bằng \frac{{a\sqrt 2 }}{2}. Tính thể tích V của khối chóp đã cho. 

     

    Gọi H là hình chiếu của A trên SB \Rightarrow AH \bot SB

    Ta có \left\{ \begin{gathered} SA \bot \left( {ABCD} ight) \Rightarrow SA \bot BC \hfill \\ AB \bot BC \hfill \\ \end{gathered} ight.

    \Rightarrow BC \bot \left( {SAB} ight) \Rightarrow AH \bot BC

    Suy ra AH \bot \left( {SBC} ight) \Rightarrow d\left[ {A,\left( {SBC} ight)} ight] = AH = \frac{{a\sqrt 2 }}{2}

    Tam giác SAB vuông tại A, có \frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} \Rightarrow SA = a

    Vậy V = \frac{1}{3}.SA.{S_{ABCD}} = \frac{{{a^3}}}{3}.

  • Câu 6: Thông hiểu

    Số cạnh của hình đa diện luôn luôn là một số tự nhiên

     Có thể lấy tứ diện làm đại diện để xét với số đỉnh là 4, số cạnh là 6 và số mặt là 4.

  • Câu 7: Thông hiểu

    Gọi Đ là số các đỉnh, M là số các mặt, C là số các cạnh của một hình đa diện bất kỳ. Mệnh đề nào sau đây là đúng?

    Xét hình đa diện là một hình bất kì, ví dụ lấy đa diện là hình tứ diện thì ta có số đỉnh, mặt và cạnh lần lượt là:

    Đ=4; M=4; C=6

  • Câu 8: Nhận biết

    Trong các mệnh đề sau, mệnh đề nào saì?

    Áp dụng khái niệm đa diện lồi, ta thấy hình hộp, tứ diện, lập phương đều là các đa diện lồi. Xét đáp án còn lại, ta có: 

    - Hai tứ diện đều ghép vào nhau có thể không tạo thành một hình đa diện lồi.

    - Hai tứ diện (đều là các đa diện lồi) nhưng khi ghép với nhau có thể không tạo thành một hình đa diện lồi.

  • Câu 9: Thông hiểu

    Cho các hình khối sau:

    Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là?

    2 || Hai || hai

    Đáp án là:

    Cho các hình khối sau:

    Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là?

    2 || Hai || hai

     Có hai khối đa diện lồi là: Hình 1 & Hình 4

  • Câu 10: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là trung điểm của các cạnh AB và AD; H là giao điểm của CN và DM. Biết SH vuông góc với mặt phẳng (ABCD) và SH =a \sqrt 3. Tính thể tích khối chóp S.CDNM.

     

    Theo giả thiết, ta có SH = a\sqrt 3.

    Diện tích tứ giác:

    {S_{CDNM}} = {S_{ABCD}} - {S_{\Delta AMN}} - {S_{\Delta BMC}}

    = A{B^2} - \frac{1}{2}AM.AN - \frac{1}{2}BM.BC = {a^2} - \frac{{{a^2}}}{8} - \frac{{{a^2}}}{4} = \frac{{5{a^2}}}{8}

    Vậy  {V_{S.CDNM}} = \frac{1}{3}{S_{CDNM}}.SH = \frac{{5{a^3}\sqrt 3 }}{{24}}.

  • Câu 11: Thông hiểu

    Khối lăng trụ ngũ giác có bao nhiêu cạnh?

    Khối lăng trụ ngũ giác có số cạnh của một mặt đáy là 5 cạnh, số cạnh bên là 5 cạnh

    Số cạnh của khối lăng trụ ngũ giác là: 2.5 + 5 =15 cạnh.

  • Câu 12: Vận dụng

    Số mặt phẳng đối xứng của hình bát diện đều là:

    Gọi bát diện đều là ABCDEF

    Hình bát diện đều

    Có 9 mặt phẳng đối xứng, bao gồm: 3 mặt phẳng (ABCD), (BEDF), (AECF) và 6 mặt phẳng mà mỗi mặt phẳng là mặt phẳng trung trực của hai cạnh song song (chẳng hạn AB và CD).

  • Câu 13: Thông hiểu

    Tổng độ dài \ell của tất cả các cạnh của một tứ diện đều cạnh a.

     

    Tứ diện đều có tất cả cạnh nên có tổng độ dài các cạnh là  \ell = 6a

  • Câu 14: Vận dụng

    Tổng các góc ở đỉnh của tất cả các mặt của khối đa diện đều loại \left\{ {3;5} ight\} là:

    Khối đa diện đều loại \left\{ {3;5} ight\} là khối hai mươi mặt đều:

    Gồm 20 mặt là các tam giác đều nên tổng các góc bằng: 20.\pi = 20\pi

  • Câu 15: Nhận biết

    Cho các hình sau: Tìm hình đa diện

    Mỗi hình sau gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:

    Áp dụng định nghĩa hình đa diện, ta có:

    “Hình đa diện (còn gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác, gọi là các mặt của hình đa diện, thỏa mãn các tính chất sau:

    TC1: Hai mặt phân biệt chỉ có thể hoặc không giao nhau hoặc có một đỉnh chung, hoặc có một cạnh chung.

    TC2: Mỗi cạnh thuộc một mặt là cạnh cung của đúng hai mặt.

    TC3: Cho hai mặt S và S’, luôn tồn tại một dãy các mặt {S_0},{S_1},...\,\,,{S_n} sao cho trùng với trùng với S’ và bất kì hai mặt {S_i},{S_{i + 1}} nào (0 \le i \le n - 1) cũng đều có một cạnh chung.

    Các đỉnh, cạnh của mặt theo thứ tự được gọi là các đỉnh, cạnh của hình đa diện.”

  • Câu 16: Vận dụng

    Cho khối đa diện đều loại \{ 3; 4 \}. Tổng các góc phẳng tại một đỉnh của khối đa điện đó bằng?

     Khối đa diện đều loại \{ 3; 4 \} là khối bát diện đều.

    Mỗi đỉnh là đỉnh chung của 4 mặt.

    Vậy tổng các góc phẳng tại một đỉnh của khối đa diện đó bằng 60^∘⋅4=240^∘.

  • Câu 17: Nhận biết

    Trong các mệnh đề sau, mệnh đề nào sai?

     Trong 5 loại khối đa diện đều không tồn tại khối chóp có đáy là tứ giác!

  • Câu 18: Thông hiểu

    Tính thể tích V của khối lăng trụ tam giác đều có cạnh đáy bằng a và tổng diện tích các mặt bên bằng 3a^2

     

    Xét khối lăng trụ ABC.A'B'C'có đáy ABC là tam giác đều và AA' \bot \left( {ABC} ight).

    Diện tích xung quanh lăng trụ là {S_{xq}} = 3.{S_{ABB'A'}}

    \Leftrightarrow 3{a^2} = 3.\left( {AA'.AB} ight) \Leftrightarrow 3{a^2} = 3.\left( {AA'.a} ight) \Rightarrow AA' = a

    Diện tích tam giác ABC là {S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{4}.

    Vậy thể tích khối lăng trụ là {V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{{a^3}\sqrt 3 }}{4}.

  • Câu 19: Thông hiểu

    Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của khối chóp đã cho.

     

    Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Vì S.ABC là khối chóp đều nên suy ra \,SI \bot \left( {ABC} ight).

    Gọi M là trung điểm của BC\,\, \Rightarrow \,\,AI = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}

    Tam giác SAI vuông tại I, có:

    SI = \sqrt {S{A^2} - S{I^2}} = \sqrt {{{\left( {2a} ight)}^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} ight)}^2}} = \frac{{a\sqrt {33} }}{3}

    Diện tích tam giác ABC là:  {S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{4}

    Vậy thể tích khối chóp:  {V_{S.ABCD}} = \frac{1}{3}{S_{\Delta ABC}}.SI = \frac{{\sqrt {11} \,{a^3}}}{{12}}

  • Câu 20: Nhận biết

    Mệnh đề nào sau đây đúng?

     Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ sau:

    - Khối lập phương có 6 mặt.

    \Rightarrow "Mọi khối đa diện đều có số mặt là những số chia hết cho 4" \Rightarrow Sai.

    - Khối lập phương và khối bát diện đều có cùng số cạnh là 12. \Rightarrow Đúng

    - Khối tứ diện đều không có tâm đối xứng.

    \Rightarrow "Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng": Sai.

    - Khối 12 mặt đều có 20 đỉnh. Khối 20 mặt đều có 12 đỉnh.

    \Rightarrow "Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh": Sai

     

  • Câu 21: Thông hiểu

    Trong các hình dưới đây, hình nào không phải đa diện lồi?

     Áp dụng dấu hiệu nhận biết của khối đa diện lồi (H): Đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Ta thấy có hình sau vi phạm tính chất đó:

     

  • Câu 22: Nhận biết

    Khái niệm chính xác nhất về khối đa diện là:

     Áp dụng định nghĩa khối đa diện, ta có:

    “Khối đa diện là phần không gian được giới hạn bởi 1 hình đa diện, kể cả hình đa diện đó.”

  • Câu 23: Nhận biết

    Hình đa diện trong hình vẽ dưới đây có bao nhiêu mặt ?

     Quan sát hình vẽ và đếm các mặt xung quanh, chú ý cả những mặt được vẽ bằng nét đứt, không nhìn thấy được. 

  • Câu 24: Thông hiểu

    Chọn khẳng định đúng trong các khẳng định sau:

    Tâm tất cả các mặt của một hình tứ diện đều là các đỉnh của một hình tứ diện đều:

  • Câu 25: Nhận biết

    Tổng số cạnh của các loại hình {3;4} và {5;3} là bao nhiêu?

     Hình {3;4} là khối bát diện đều, có 12 cạnh.

    Hình {5;3} là khối mười hai mặt đều, có 30 cạnh.

    Vậy tổng số cạnh của hai hình trên là 12 + 30 =42 cạnh.

  • Câu 26: Thông hiểu

    Trung điểm các cạnh của một tứ diện đều tạo thành?

     Trung điểm các cạnh của một tứ diện đều tạo thành các đỉnh của một hình bát diện đều:

  • Câu 27: Nhận biết

    Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a?

     

    Xét khối lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a.

  • Câu 28: Vận dụng

    Có tất cả bao nhiêu mặt phẳng cách đều bốn đỉnh của một tứ diện?

    Có 2 loại mặt phẳng thỏa mãn đề bài là:

    a) Loại 1: Mặt phẳng qua trung điểm của 3 cạnh bên có chung đỉnh. Có 4 mặt phẳng thỏa mãn loại này (vì có 4 đỉnh)

    Mp cách đều 4 đỉnh

    Nhận xét. Loại này ta thấy có 1 điểm nằm khác phía với 3 điểm còn lại.

    b) Loại 2: Mặt phẳng qua trung điểm của cạnh ( cạnh này thuộc cặp cạnh, mỗi cặp cạnh là chéo nhau). Có mặt phẳng như thế.

    Mp cách đều 4 đỉnh

    Nhận xét. Loại này ta thấy có 2 điểm nằm khác phía với 2 điểm còn lại.

  • Câu 29: Nhận biết

    Cho lăng trụ đứng ABC.A'B'C'có đáy ABC là tam giác với AB = a,AC = 2a,\widehat {BAC} = {120^0},AA' = 2a\sqrt 5. Tính thể tích Vcủa khối lăng trụ đã cho.

     

    Diện tích tam giác ABC là {S_{\Delta ABC}} = \frac{1}{2}AB.AC.\sin \widehat {BAC} = \frac{{{a^2}\sqrt 3 }}{2}.

    Vậy thể tích khối lăng trụ {V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = {a^3}\sqrt {15}

  • Câu 30: Nhận biết

    Cho hình chóp S.ABC có tam giác SBC là tam giác vuông cân tại S, SB=2a  và khoảng cách từ A đến mặt phẳng (SBC) bằng 3a. Tính theo a thể tích V của khối chóp S.ABC.

     Ta chọn (SBC) làm mặt đáy suy ra chiều cao khối chóp là d\left[ {A,\left( {SBC} ight)} ight] = 3a

    Tam giác SBC vuông cân tại  S nên {S_{\Delta SBC}} = \frac{1}{2}S{B^2} = 2{a^2}

    Vậy thể tích khối chóp V = \frac{1}{3}{S_{\Delta SBC}}.d\left[ {A,\left( {SBC} ight)} ight] = 2{a^3}

  • Câu 31: Vận dụng

    Tổng các góc ở đỉnh của tất cả các mặt của khối đa diện đều loại \left\{ {4;3} ight\} là:

    Khối đa diện đều loại \left\{ {4;3} ight\} là khối lập phương, gồm 6 mặt là các hình vuông nên tổng các góc bằng:  6.2\pi = 12\pi

  • Câu 32: Vận dụng cao

    Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều. Cạnh đáy dưới dài 5 m, cạnh đáy trên dài 2 m, cạnh bên dài 3 m. Biết rằng chân tháp được làm bằng bê tông tươi với giá tiền là 1 470 000 đồng/m3. Tính số tiền để mua bê tông tươi làm chân tháp theo đơn vị chục nghìn.

    Đáp án: 4054 (chục nghìn)

    Đáp án là:

    Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều. Cạnh đáy dưới dài 5 m, cạnh đáy trên dài 2 m, cạnh bên dài 3 m. Biết rằng chân tháp được làm bằng bê tông tươi với giá tiền là 1 470 000 đồng/m3. Tính số tiền để mua bê tông tươi làm chân tháp theo đơn vị chục nghìn.

    Đáp án: 4054 (chục nghìn)

    Hình vẽ minh họa

    Mô hình hóa chân tháp của bài toán bằng khối chóp cụt tứ giác đều ABCD.A^{'}B^{'}C^{'}D^{'}, với O,O^{'} lần lượt là tâm của hai đáy ABCD và A^{'}B^{'}C^{'}D^{'}.

    Như vậy ta có:

    ABCD là hình vuông cạnh 5 có diện tích S_{ABCD} = 5^{2} = 25;

    A^{'}B^{'}C^{'}D^{'} là hình vuông cạnh 2 có diện tích S_{A^{'}B^{'}C^{'}D^{'}} = 2^{2} = 4;

    Các cạnh bên A^{'}A,B^{'}B,C^{'}C,D^{'}D có độ dài bằng 3;

    {OO}^{'} vuông góc với ( ABCD ) và ( \left. \ A^{'}B^{'}C^{'}D^{'} ight).

    Do ABCD là hình vuông nên \widehat{ABC} =90^{\circ}, do đó tam giác ABC vuông tại B.

    Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:

    AC^{2} = AB^{2} + BC^{2} = 5^{2} + 5^{2}= 50

    Suy ra AC = 5\sqrt{2}.
    Do đó CO = \frac{AC}{2} =\frac{5\sqrt{2}}{2} (do 0 là tâm hình vuông ABCD ).

    Do A^{'}B^{'}C^{'}D^{'} là hình vuông nên \widehat{A^{'}B^{'}C^{'}} = 90^{\circ}, do đó tam giác A^{'}B^{'}C^{'} vuông tại B^{'}.

    Áp dụng định lí Pythagore trong tam giác A^{'}B^{'}C^{'} vuông tại B^{'} có:

    A^{'}C^{'2} = A^{'}B^{'2} + B^{'}C^{'2} = 2^{2} + 2^{2} = 8.

    Suy ra A^{'}C^{'} = 2\sqrt{2}.

    Do đó C^{'}O^{'} = \frac{A^{'}C^{'}}{2} = \frac{2\sqrt{2}}{2} = \sqrt{2} (do O^{'} là tâm hình vuông A^{'}B^{'}C^{'}D^{'} ).

    Dễ thấy: (ABCD) \cap \left( A^{'}C^{'}CA ight) = AC; \left( A^{'}B^{'}C^{'}D^{'} ight) \cap \left( A^{'}C^{'}CA ight) = A^{'}C^{'}.

    Mà ( ABCD ) // ( \left. \ A^{'}B^{'}C^{'}D^{'} ight).

    Suy ra AC//A^{'}C^{'} hay A^{'}C^{'}CA là hình thang.

    Xét hình thang A^{'}C^{'}CA, kẻ C^{'}H\bot AC(H \in AC).

    Vì 00^{'}\bot(ABCD) và AC \subset (ABCD) nên 00^{'}\bot AC.

    Do đó C^{'}H//{OO}^{'} (cùng vuông góc với AC).

    Mà O^{'}C^{'}//OH (do A^{'}C^{'}//AC )

    Suy ra O^{'}C^{'}HO là hình bình hành.

    Do đó: 0O^{'} = C^{'}H và OH = C^{'}O^{'} = \sqrt{2}.

    Suy ra HC = OC - OH = \frac{5\sqrt{2}}{2} - \sqrt{2} = \frac{3\sqrt{2}}{2}.

    Áp dụng định lí Pythagore trong tam giác C^{'}HC vuông tại H( do \left. \ C^{'}H\bot AC ight) có:

    C^{'}C^{2} = C^{'}H^{2} + {HC}^{2}

    Suy ra C^{'}H = \sqrt{C^{'}C^{2} - HC^{2}} = \sqrt{3^{2} - \left( \frac{3\sqrt{2}}{2} ight)^{2}} = \frac{3\sqrt{2}}{2}.

    Do đó OO^{'} = C^{'}H = \frac{3\sqrt{2}}{2}.

    Thể tích khối chóp cụt tứ giác đều ABCD.A^{'}B^{'}C^{'}D^{'} với chiều cao OO^{'} = \frac{3\sqrt{2}}{2} và diện tích hai đáy S_{ABCD} = 25, S_{A'B'C'D'} =4 là:

    V_{ABCD \cdot A^{'}B^{'}C^{'}D^{'}} = \frac{1}{3} \cdot\frac{3\sqrt{2}}{2}(25 + \sqrt{25.4} + 4) = \frac{39\sqrt{2}}{2}\left({m}^{3} ight)

    Như vậy ta có thể tích của chân tháp đã cho bằng \frac{39\sqrt{2}}{2}\left( {m}^{3}ight).

    Vi chân tháp được làm bằng bê tông tươi với giá tiền là 1470000 đồng /m^{3} nên số tiền để mua bê tông tươi làm chân tháp là:

    \frac{39\sqrt{2}}{2}.1470000 \approx40538432 (đồng)

    Vậy số tiền để mua bê tông tươi làm chân tháp khoảng 40538432 đồng.

  • Câu 33: Vận dụng cao

    Cho hình hộp chữ nhật có đường chéo d = \sqrt {21}. Độ dài ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân có công bội q=2. Thể tích của khối hộp chữ nhật là?

    Xét hình hộp chữ nhật ABCD.A'B'C'D'có độ dài kích thước ba cạnh lần lượt là AA' = a,\,\,AB = b,\,\,AD = c và có đường chéo AC'.

    Theo bài ra, ta có a, b, c lập thành cấp số nhân có công bội q=2. Suy ra:

    \left\{ \begin{gathered} b = 2a \hfill \\ c = 4a \hfill \\ \end{gathered} ight.

    Mặt khác, độ dài đường chéo AC' = \sqrt {21}

    \Rightarrow A{A'^2} + A{B^2} + A{D^2} = 21\Leftrightarrow {a^2} + {b^2} + {c^2} = 21

    Ta có hệ:

    \left\{ \begin{gathered} c = 2b = 4a \hfill \\ {a^2} + {b^2} + {c^2} = 21 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} c = 2b = 4a \hfill \\ {a^2} + {\left( {2a} ight)^2} + {\left( {4a} ight)^2} = 21 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} c = 2b = 4a \hfill \\ 21{a^2} = 21 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} a = 1 \hfill \\ b = 2 \hfill \\ c = 4 \hfill \\ \end{gathered} ight.

    Vậy thể tích khối hộp chữ nhật ABCD.A'B'C'D'là:

    {V_{ABCD.A'B'C'D'}} = AA'.AB.AD = abc = 8

  • Câu 34: Vận dụng cao

    Hình lăng trụ có thể có số cạnh nào sau đây?

    Giả sử hình lăng trụ có đáy là n – giác.

    Khi đó, số cạnh của hình lăng trụ là 3n.

    Như vậy số cạnh của hình lăng trụ phải chia hết cho 3, xét các đáp án thì chỉ có 2022 chia hết cho 3 nên số cạnh của hình lăng trụ chỉ có thể là 2022.

  • Câu 35: Thông hiểu

    Cho một hình đa diện. Trong các khẳng định sau, khẳng định nào sai?

    Áp dụng định nghĩa hình đa diện, ta có:

    “Hình đa diện (còn gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác, gọi là các mặt của hình đa diện, thỏa mãn các tính chất sau:

    TC1: Hai mặt phân biệt chỉ có thể hoặc không giao nhau hoặc có một đỉnh chung, hoặc có một cạnh chung.

    TC2: Mỗi cạnh thuộc một mặt là cạnh cung của đúng hai mặt.

    TC3: Cho hai mặt S và S’, luôn tồn tại một dãy các mặt S_0, S_1,... , S_n sao cho S_0 trùng với S, S_n trùng với S’ và bất kì hai mặt nào cũng đều có một cạnh chung.

    Các đỉnh, cạnh của mặt theo thứ tự được gọi là các đỉnh, cạnh của hình đa diện.”

    Ta thấy ngoai trừ "Mỗi cạnh là cạnh chung của ít nhất ba mặt" các đáp án còn lại  đều đúng dựa vào khái niệm hình đa diện.

  • Câu 36: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh AB=a, BC =2a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy (ABCD). Tính theo a thể tích V của khối chóp S.ABCD.

     

    Vì hai mặt bên (SAB) và (SAD) cùng vuông góc với (ABCD), suy ra SA \bot \left( {ABCD} ight). Do đó chiều cao khối chóp là SA = a\sqrt {15}.

    Diện tích hình chữ nhật ABCD là {S_{ABCD}} = AB.BC = 2{a^2}

    Vậy thể tích khối chóp {V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SA = \frac{{2{a^3}\sqrt {15} }}{3}

  • Câu 37: Vận dụng

    Cho hình chóp đều S.ABC có tất cả các cạnh bằng a. Mặt phẳng (P) song song với mặt đáy (ABC) và cắt các cạnh bên SA, SB, SC lần lượt tại M, N, P. Tính diện tích tam giác MNP biết mặt phẳng (P) chia khối chóp đã cho thành hai phần có thể tích bằng nhau. 

     

    Mặt phẳng \left( P ight)\parallel \left( {ABC} ight) và cắt các cạnh SA,\,\,SB,\,\,SC lần lượt tại M,\,\,N,\,\,P.

    Theo Talet, ta có \frac{{SM}}{{SA}} = \frac{{SN}}{{SB}} = \frac{{SP}}{{SC}} = x.

    Do đó \frac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}}.\frac{{SP}}{{SC}} = {x^3}.

    Theo giả thiết \frac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \frac{1}{2} \to {x^3} = \frac{1}{2} \to x = \frac{1}{{\sqrt[3]{2}}}.

    Suy ra tam giác MNP là tam giác đều cạnh \frac{a}{{\sqrt[3]{2}}}. 

    Vậy diện tích {S_{\Delta MNP}} = {\left( {\frac{a}{{\sqrt[3]{2}}}} ight)^2}.\frac{{\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{{4\sqrt[3]{4}}}.

  • Câu 38: Vận dụng

    Cho hình lăng trụ ABC.A'B'C'có đáy là tam giác đều cạnh có độ dài bằng 2. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trung điểm H của BC. Góc tạo bởi cạnh bên AA' với mặt đáy là 45^0. Tính thể tích khối trụ  ABC.A'B'C'.

    3 || Ba || ba || V=3

    Đáp án là:

    Cho hình lăng trụ ABC.A'B'C'có đáy là tam giác đều cạnh có độ dài bằng 2. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trung điểm H của BC. Góc tạo bởi cạnh bên AA' với mặt đáy là 45^0. Tính thể tích khối trụ  ABC.A'B'C'.

    3 || Ba || ba || V=3

     

    Tam giác đều ABC cạnh bằng 2 nên AH = \sqrt 3.

    Vì A'H \bot \left( {ABC} ight) nên hình chiếu vuông góc của AA' trên mặt đáy (ABC) là AH. 

    Do đó {45^0} = \widehat {AA',\left( {ABC} ight)} = \widehat {AA',AH} = \widehat {A'AH}.

    Suy ra tam giác A'HA vuông cân tại H nên A'H = HA = \sqrt 3.

    Diện tích tam giác đều ABC là {S_{\Delta ABC}} = \sqrt 3.

    Vậy V = {S_{\Delta ABC}}.A'H = 3.

  • Câu 39: Vận dụng

    Cho hình đa diện đều loại \left\{ {4;3} ight\} cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình đa diện đó. Mệnh đề nào dưới đây đúng?

    Đa diện đều loại \left\{ {4;3} ight\} là khối lập phương nên có 6 mặt là các hình vuông cạnh a.

    Vậy hình lập phương có tổng diện tích tất cả các mặt là S=6a^2

  • Câu 40: Thông hiểu

    Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy bằng 60^{0}. Thể tích V của khối chóp S.ABCD bằng

    Hình vẽ minh họa

    Gọi O là tâm của đáy, gọi M là trung điểm của BC.

    Ta có \left\{ \begin{matrix} SO\bot BC \\ OM\bot BC \\ \end{matrix} ight. nên (SOM)\bot BC

    Suy ra \left\lbrack (SCD),(ABCD) ightbrack = (SM,OM) = \widehat{SMO} = 60^{0}.

    Có OM = \frac{1}{2}BC = \frac{a}{2}, SO = OMtan60^{0} = \frac{a\sqrt{3}}{2}.

    Thể tích khối chóp S.ABCD là

    V_{S.ABCD} = \frac{1}{3}SO.S_{ABCD} = \frac{1}{3}.\frac{a\sqrt{3}}{2}.a^{2} = \frac{a^{3}\sqrt{3}}{6}.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 1 Khối đa diện Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án
Làm lại
  • 17 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 45 phút Chương 1 Khối đa diện
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập