Lớp 12 Toán 12

Đề kiểm tra 45 phút Chương 2 Mặt nón, mặt trụ, mặt cầu

Hãy cùng thử sức kiểm tra đánh giá các kiến thức tổng quan với bài kiểm tra phút Chương 2: Mặt trụ - Mặt nón - Mặt cầu Toán 12 các em nhé!

  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Nhận biết

    Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh bằng a. Thể tích khối trụ bằng:

     Do thiết diện đi qua trục hình trụ nên ta có h=a.

    Bán kính đáy R = \frac{a}{2}. Do đó thể tích khối trụ V = {R^2}\pi .h = \frac{{\pi {a^3}}}{4}(đvtt).

  • Câu 2: Thông hiểu

    Trong không gian Oxyz, cho mặt cầu (S):(x + 3)^{2} + (y - 1)^{2} + (z + 1)^{2} = 3 và mặt phẳng (\alpha):(m - 4)x + 3y - 3mz + 2m - 8 = 0. Với giá trị nào của tham số m thì mặt phẳng tiếp xúc với mặt cầu?

    Mặt cầu (S) có tâm I(−3; 1; −1) và bán kính R = \sqrt{3}

    Mặt phẳng (α) tiếp xúc với (S) khi và chỉ khi

    d\left( I;(P) ight) = R

    \Leftrightarrow \frac{\left| (m - 4).( - 3) + 3.1 - 3m.( - 1) + 2m - 8 ight|}{\sqrt{(m - 4)^{2} + 3^{2} + ( - 3m)^{2}}} = \sqrt{3}

    \Leftrightarrow \frac{|2m + 7|}{\sqrt{10m^{2} - 8m + 25}} = \sqrt{3}

    \Leftrightarrow 26m^{2} - 52m + 26 = 0 \Leftrightarrow m = 1

    Vậy đáp án cần tìm là: m = 1.

  • Câu 3: Nhận biết

    Cạnh bên của một hình nón bằng 2a. Thiết diện qua trục của nó là một tam giác cân có góc ở đỉnh bằng 120^0. Diện tích toàn phần của hình nón là:

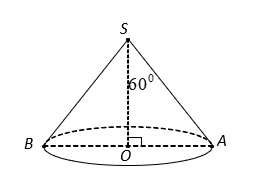
    Diện tích toàn phần

    Gọi S là đỉnh, O là tâm của đáy, thiết diện qua trục là SAB.

    Theo giả thiết, ta có SA = 2a và \widehat {ASO} = 60^\circ.

    Trong tam giác SAO vuông tại O, ta có

    OA = SA.\sin 60^\circ = a\sqrt 3

    Vậy diện tích toàn phần:

    {S_{tp}} = \pi R\ell + \pi {R^2} = \pi .OA.SA + \pi {\left( {OA} ight)^2} = \pi {a^2}\left( {3 + 2\sqrt 3 } ight) (đvdt).

  • Câu 4: Vận dụng

    Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính bằng chiều cao và bằng a. Trên đường tròn tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B sao cho AB = 2a. Thể tích của khối tứ diện OO’AB bằng:

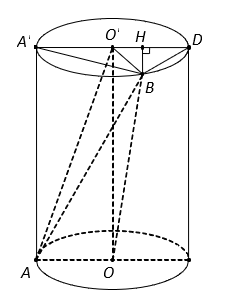
     Tính thể tích khối trụ

    Kẻ đường sinh AA’, gọi D là điểm đối xứng với A’ qua tâm O’ và H là hình chiếu của B trên A’D.

    Ta có BH \bot \left( {AOO'A'} ight) nên {V_{OO'AB}} = \frac{1}{3}{S_{\Delta AOO'}}.BH.

    Trong tam giác vuông A'AB có A'B = \sqrt {A{B^2} - AA{'^2}} = \sqrt 3 a.

    Trong tam giác vuông A'BD có BD = \sqrt {A'{D^2} - A'{B^2}} = a.

    Do đó suy ra tam giác BO'D nên BH = \frac{{\sqrt 3 a}}{2}.

    Vậy  {V_{OO'AB}} = \frac{1}{3}.\left( {\frac{1}{2}{a^2}} ight).\frac{{a\sqrt 3 }}{2} = \frac{{\sqrt 3 {a^3}}}{{12}} (đvtt).

  • Câu 5: Nhận biết

    Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):x^{2} + y^{2} + z^{2} + 2x - 2z - 7 = 0. Bán kính của mặt cầu (S) là:

    Ta có:

    x^{2} + y^{2} + z^{2} + 2x - 2z - 7 = 0

    \Leftrightarrow x^{2} + y^{2} + z^{2} - 2.( - 1)x - 2.0.y - 2.1z - 7 = 0

    \Leftrightarrow \left\{ \begin{matrix} a = - 1 \\ b = 0 \\ c = 1 \\ d = - 7 \\ \end{matrix} ight. suy ra tâm mặt cầu là: I( - 1;0;1)

    Bán kính mặt cầu là:

    R = \sqrt{a^{2} + b^{2} + c^{2} - d} = \sqrt{( - 1)^{2} + 0^{2} + 1^{2} - 7} = 3

  • Câu 6: Vận dụng cao

    Trong không gian Oxyz, cho điểm A(1;2;-1) và mặt phẳng (P):x+y+2z-13=0. Xét các mặt cầu (S) có tâm I(a;b;c), đi qua điểm A, tiếp xúc với mặt phẳng (P) . Tính giá trị của biểu thức T=a^2+2b^2+3c^2 khi (S) có bán kính nhỏ nhất.

     Gọi H là hình chiếu của I trên mặt phẳng (P) ta có IA + IH =2R nên R nhỏ nhất khi I, A, H thẳng hàng và I là trung điểm của AH.

    Phương trình AH đi qua A và vuông góc với mặt phẳng (P) có phương trình là

    \left\{\begin{matrix} x=1+t \\ y=2+t \\ z=-1+2t \end{matrix}ight.

    Tọa độ H là nghiệm (x;y;z) của hệ:

    \left\{\begin{matrix} x=1+t \\ y=2+t \\ z=-1+2t \\ x+y+2z-13=0 \end{matrix}ight.

    \Rightarrow H(3;4;3)\Rightarrow I(2;3;1)

    Suy ra, ta có: T=a^2+2b^2+3c^2 =2^2+2.3^2+3.1^2=25

  • Câu 7: Thông hiểu

    Trong không gian với hệ tọa độ Oxyz, cho điểm H(1; 2; −2). Gọi (P) là mặt phẳng đi qua H và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho H là trực tâm của tam giác ABC. Viết phương trình mặt cầu tâm O và tiếp xúc với (P).

    Hình vẽ minh họa

    Vì H là trực tâm tam giác ABC nên AH ⊥ BC, CH ⊥ AB

    \Rightarrow \left\{ \begin{matrix} AB\bot(OHC) \\ BC\bot(AHO) \\ \end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix} (ABC)\bot(OHC) \\ (ABC)\bot(AHO) \\ \end{matrix} ight.\ \Rightarrow OH\bot(ABC)

    Do vậy mặt cầu tâm O tiếp xúc với (P) nhận OH làm bán kính

    ⇒ Phương trình mặt cầu là x^{2} + y^{2} + z^{2} = 9.

  • Câu 8: Vận dụng cao

    Trong không gian Oxyz, cho mặt cầu (S): x^2 +y^2 +z^2 −2x+ 2z −2 = 0 và các điểm A(0; 1; 1), B(−1; −2; −3), C(1; 0; −3). Điểm D thuộc mặt cầu (S). Thể tích lớn nhất của tứ diện ABCD bằng:

    Mặt cầu (S) có tâm là I(1; 0; −1) và bán kính R = 2.

    Khi V_{DABC} lớn nhất thì \frac{V_{DABC}}{V_{IABC}} = \frac{d\left( D;(ABC) ight)}{d\left( I;(ABC) ight)} = \frac{R + d\left( I;(ABC) ight)}{d\left( I;(ABC) ight)}

    Ta có: \left\{ \begin{matrix} \overrightarrow{AB} = ( - 1; - 3; - 4) \\ \overrightarrow{AC} = (1; - 1; - 4) \\ \overrightarrow{AI} = (1; - 1; - 2) \\ \end{matrix} ight. suy ra:

    V_{IABC} = \frac{1}{6}\left| \left\lbrack \left\lbrack \overrightarrow{AB};\overrightarrow{AC} ightbrack.\overrightarrow{AI} ightbrack ight| = \frac{4}{3}

    \Rightarrow d\left( I;(ABC) ight) = \frac{6.V_{IABC}}{\left| \left\lbrack \overrightarrow{AB};\overrightarrow{AC} ightbrack ight|} = \frac{2}{3}

    \Rightarrow V_{DABC} =\dfrac{4}{3}.\dfrac{2 + \dfrac{2}{3}}{\dfrac{2}{3}} =\dfrac{16}{3}.

  • Câu 9: Vận dụng

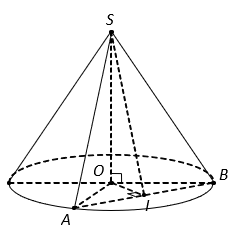
    Cho hình nón đỉnh S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và \widehat {SAO} = {30^0},\widehat {SAB} = {60^0}. Độ dài đường sinh \ell của hình nón bằng:

     Độ dài đường sinh

    Gọi I là trung điểm AB, suy ra OI \bot AB,{m{ }}SI \bot AB và OI = a.

    Trong tam giác vuông SOA, ta có OA = SA.\cos \widehat {SAO} = \frac{{SA\sqrt 3 }}{2}

    Trong tam giác vuông SIA, ta có IA = SA.\cos \widehat {SAB} = \frac{{SA}}{2}

    Trong tam giác vuông OIA, ta có:

    O{A^2} = O{I^2} + I{A^2} \Leftrightarrow \frac{3}{4}S{A^2} = {a^2} + \frac{1}{4}S{A^2} \Rightarrow SA = a\sqrt 2 .

  • Câu 10: Thông hiểu

    Một hình trụ có bán kính đáy R = 70{m{cm}} , chiều cao hình trụ h = 20{m{cm}}. Một hình vuông có các đỉnh nằm trên hai đường tròn đáy sao cho có ít nhất một cạnh không song song và không vuông góc với trục hình trụ. Khi đó cạnh của hình vuông bằng bao nhiêu?

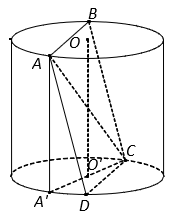
    Tính độ dài cạnh

    Xét hình vuông ABCD có AD không song song và không vuông góc với trục OO’ của hình trụ.

    Dựng đường sinh AA', ta có \left\{ \begin{array}{l}CD \bot AA'\\CD \bot AD\end{array} ight. \Rightarrow CD \bot \left( {AA'D} ight) \Rightarrow CD \bot A'D.

    Suy ra A’C là đường kính đáy nên A'C = 2R = 140{m{cm}}{m{.}}

    Xét tam giác vuông AA’C, ta có AC = \sqrt {AA{'^2} + A'{C^2}} = 100\sqrt 2 {m{cm}}{m{.}}

    Suy ra cạnh hình vuông bằng 100 cm.

  • Câu 11: Thông hiểu

    Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chu vi đáy bằng 2a thì thể tích của nó bằng:

     Gọi bán kính đáy là R.

    Hình trụ có chu vi đáy bằng 2a nên ta có 2\pi R = 2a \Leftrightarrow R = \frac{a}{\pi }.

    Suy ra hình trụ này có đường cao h=a.

    Vậy thể tích khối trụ V = \pi {R^2}h = \pi {\left( {\frac{a}{\pi }} ight)^2}a = \frac{{{a^3}}}{\pi }(đvtt).

  • Câu 12: Nhận biết

    Trong không gian Oxyz, cho mặt cầu (S):(x + 3)^{2} + (y + 1)^{2} + (z - 1)^{2} = 2 có tọa độ tâm I là:

    Tâm của (S) có tọa độ là I( - 3; - 1;1).

  • Câu 13: Vận dụng

    Một quả bóng rổ được đặt ở một góc của căn phòng hình hộp chữ nhật, sao cho quả bóng chạm và tiếp xúc với hai bức tường và nền nhà của căn phòng đó thì có một điểm trên quả bóng có khoảng cách lần lượt đến hai bức tường và nền nhà là 17 cm, 18 cm, 21 cm (tham khảo hình minh họa). Hỏi độ dài đường kính của quả bóng bằng bao nhiêu cm, biết rằng quả bóng rổ tiêu chuẩn có đường kính từ 23 cm đến 24,5 cm? (Kết quả là tròn đến một chữ số thập phân)

    A basketball on the groundDescription automatically generated

    Trả lời: 23,9 cm

    Đáp án là:

    Một quả bóng rổ được đặt ở một góc của căn phòng hình hộp chữ nhật, sao cho quả bóng chạm và tiếp xúc với hai bức tường và nền nhà của căn phòng đó thì có một điểm trên quả bóng có khoảng cách lần lượt đến hai bức tường và nền nhà là 17 cm, 18 cm, 21 cm (tham khảo hình minh họa). Hỏi độ dài đường kính của quả bóng bằng bao nhiêu cm, biết rằng quả bóng rổ tiêu chuẩn có đường kính từ 23 cm đến 24,5 cm? (Kết quả là tròn đến một chữ số thập phân)

    A basketball on the groundDescription automatically generated

    Trả lời: 23,9 cm

    Ta đặt hệ trục vào căn phòng sao cho có hai bức tường là mặt (Oxz),(Oyz), và nền là (Oxy)

    Vậy bài toán dẫn đến việc tìm đường kính của mặt cầu tiếp xúc với 3 mặt phẳng toạ độ và chứa điểm M(17\ ;\ 18\ ;\ 21).

    Ta có thể gọi phương trình mặt cầu là (S):(x - a)^{2} + (y - b)^{2} + (z - c)^{2} = R^{2}, với a,b,c,R > 0

    Do mặt cầu tiếp xúc với các mặt phẳng toạ độ nên a = b = c = R

    \Rightarrow (S):(x - a)^{2} + (y - a)^{2} + (z - a)^{2} = a^{2}

    Do M(17\ ;\ 18\ ;\ 21) \in (S) nên (17 - a)^{2} + (18 - a)^{2} + (21 - a)^{2} = a^{2}.

    \Rightarrow 2a^{2} - 112a + 1054 = 0 \Leftrightarrow \left\lbrack \begin{matrix} a = 28 - \sqrt{257} \\ a = 28 + \sqrt{257} \\ \end{matrix} ight.

    Vì quả bóng rổ tiêu chuẩn có đường kính từ 23 cm đến 24,5 cm nên a = 28 - \sqrt{257} thỏa.

    Vậy đường kính quả bóng bằng 2a = 56 - 2\sqrt{257} \approx 23,9\ (cm).

  • Câu 14: Vận dụng

    Một hình nón có đường cao bằng 9 cm nội tiếp trong một hình cầu bán kính bằng 5 cm. Tỉ số giữa thể tích khối nón và khối cầu là:

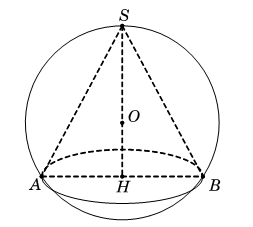
    Tỉ số giữa thể tích

    Hình vẽ kết hợp với giả thiết, ta có SH = 9cm, OS=OA=5cm

    Suy ra OH = 4{m{cm}} và AH = \sqrt {O{A^2} - O{H^2}} = 3{m{cm}}{m{.}}

    Thể tích khối nón {V_n} = \frac{1}{3}\pi A{H^2}.SH = 27\pi(đvtt).

    Thể tích khối cầu {V_c} = \frac{4}{3}\pi .S{O^3} = \frac{{500\pi }}{3}  (đvtt).

    Suy ra \frac{{{V_n}}}{{{V_c}}} = \frac{{81}}{{500}}

  • Câu 15: Nhận biết

    Trong không gian, cho tam giác ABC vuông tại A, AB =a và AC = a\sqrt 3. Độ dài đường sinh \ell của hình nón nhận được khi quay tam giác ABC xung quanh trục AB bằng:

    Độ dài đường sinh

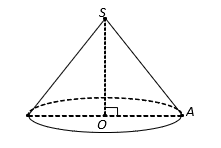
    Từ giả thiết suy ra hình nón có đỉnh là B , tâm đường tròn đáy là A , bán kính đáy là AC = a\sqrt 3 và chiều cao hình nón là AB = a.

    Vậy độ dài đường sinh của hình nón là:

    \ell = BC = \sqrt {A{B^2} + A{C^2}} = 2a.

  • Câu 16: Vận dụng cao

    Trong không gian Oxyz, , cho hai mặt cầu (S_1), (S_2) có phương trình lần lượt là (x − 2)^2 + (y − 1)^2 + (z − 1)^2 = 16 và (x − 2)^2 + (y − 1)^2 + (z − 5)^2 = 4. Gọi (P) là mặt phẳng thay đổi tiếp xúc với cả hai mặt cầu (S_1), (S_2). Tính khoảng cách lớn nhất từ gốc tọa độ O đến mặt phẳng (P).

    Hình vẽ minh họa

    Mặt cầu (S1) có tâm I(2; 1; 1) và bán kính R_1 = 4.

    Mặt cầu (S2) có tâm J(2; 1; 5) và bán kính R_2 = 2.

    Gọi A, B lần lượt là hai tiếp điểm của (S1), (S2) với mặt phẳng (P).

    Gọi M là giao điểm của IJ với mặt phẳng (P). Ta có:

    \frac{MI}{MJ} = \frac{IA}{IB} = 2

    Suy ra J là trung điểm của IM, do đó M(2; 1; 9).

    Gọi véc-tơ pháp tuyến của mặt phẳng (P) là \overrightarrow{n} = (a;b;c),\left( a^{2} + b^{2} + c^{2} > 0 ight) khi đó phương trình của mặt phẳng (P) là

    a(x − 2) + b(y − 1) + c(z − 9) = 0

    Ta có:

    d\left( I;(P) ight) = 4 \Leftrightarrow \frac{|8c|}{\sqrt{a^{2} + b^{2} + c}} = 4

    \Leftrightarrow \frac{|c|}{\sqrt{a^{2} + b^{2} + c}} = \frac{1}{2} \Leftrightarrow a^{2} + b^{2} = 3c^{2}

    \Leftrightarrow \left( \frac{a}{c} ight)^{2} + \left( \frac{b}{c} ight)^{2} = 3\ \ \ (1)

    Mặt khác d\left( O;(P) ight) = \frac{|2a + b + 9c|}{\sqrt{a^{2} + b^{2} + c^{2}}} = \frac{|2a + b + 9c|}{2c} = \frac{1}{2}\left| \frac{2a}{c} + \frac{b}{c} + 9 ight|\ \ \ (2)

    Áp dụng bất đẳng thức Bunhiacopxki ta có

    \left( \frac{2a}{c} + \frac{b}{c} ight)^{2} \leq \left( 2^{2} + 1^{2} ight)\left\lbrack \left( \frac{a}{c} ight)^{2} + \left( \frac{b}{c} ight)^{2} ightbrack\ \ \ (3)

    Từ (1) và (3) ta có: \left( \frac{2a}{c} + \frac{b}{c} ight)^{2} \leq 15 \Leftrightarrow - \sqrt{15} \leq \frac{2a}{c} + \frac{b}{c} \leq \sqrt{15}\ \ (4)

    Từ (2) và (4) suy ra:

    \frac{9 - \sqrt{15}}{2} \leq d\left( O;(P) ight) \leq \frac{9 + \sqrt{15}}{2}

    Vậy khoảng cách lớn nhất từ gốc tọa độ O đến mặt phẳng (P) bằng \frac{9 + \sqrt{15}}{2}.

  • Câu 17: Thông hiểu

    Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chiều dài đường sinh bằng 2a thì bán kính đáy bằng:

     Gọi bán kính đáy là R.

    Từ giả thiết suy ra h= 2a và chu vi đáy bằng a .

    Do đó 2\pi R = a \Leftrightarrow R = \frac{a}{{2\pi }}.

  • Câu 18: Vận dụng

    Cho mặt cầu \left( S ight):{x^2} + {y^2} + {z^2} + 4x - 2y + 6z - 2 = 0 và mặt phẳng \left( P ight):3x + 2y + 6z + 1 = 0. Gọi (C) là đường tròn giao tuyến của (P) và (S). Viết phương trình mặt cầu (S') chứa (C) và điểm M(1,-2,1)

     Phương trình của \left( {S'} ight):\left( S ight) + m\left( P ight) = 0,\,\,m e 0

    \left( {S'} ight):{x^2} + {y^2} + {z^2} + 4x - 2y + 6z - 2 + m\left( {3x + 2y + 6z + 1} ight) = 0

    (S') qua M\left( {1, - 2,1} ight) \Rightarrow 6m + 18 = 0 \Leftrightarrow m = - 3

    \Rightarrow \left( {S'} ight):{x^2} + {y^2} + {z^2} - 5x - 8y - 12z - 5 = 0

  • Câu 19: Nhận biết

    Cho hình nón đỉnh S có bán kính đáy R = a\sqrt 2, góc ở đỉnh bằng {60^0}. Diện tích xung quanh của hình nón bằng:

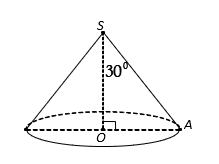
    Diện tích xung quanh

     Theo giả thiết, ta có OA = a\sqrt 2 và \widehat {OSA} = {30^0}.

    Suy ra độ dài đường sinh:  \ell = SA = \frac{{OA}}{{\sin {{30}^0}}} = 2a\sqrt 2

    Vậy diện tích xung quanh bằng: {S_{xq}} = \pi R\ell = 4\pi {a^2} (đvdt). 

  • Câu 20: Vận dụng cao

    Cho hình nón có bán kính đáy là 5a , độ dài đường sinh là 13a. Thể tích khối cầu nội tiếp hình nón bằng:

    Thể tích khối cầu nội tiếp hình nón

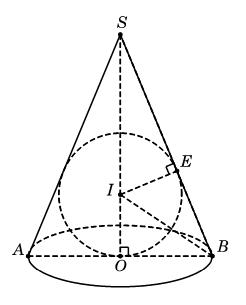
    Xét mặt phẳng qua trục SO của hình nón ta được thiết diện là tam giác cân SAB.

    Mặt phẳng đó cắt mặt cầu theo đường tròn có bán kính r (bán kính mặt cầu) và nội tiếp trong tam giác cân SAB.

    Trong tam giác vuông SOB, gọi I là giao điểm của đường phân giác trong góc B với đường thẳng SO.

    Chứng minh được I là tâm đường tròn nội tiếp tam giác và bán kínhr =IO=IE  (E là hình chiếu vuông góc của I trên SB).

    Theo tính chất phân giác, ta có \frac{{IS}}{{IO}} = \frac{{BS}}{{BO}} = \frac{{13}}{5}.

    Lại có IS + IO = SO = \sqrt {S{B^2} - O{B^2}} = 12.

    Từ đó suy ra IS = \frac{{26}}{3},{m{ }}IO = \frac{{10}}{3}.

    Ta có \Delta SEI \backsim\Delta SOB  nên \frac{{IE}}{{IS}} = \frac{{BO}}{{BS}} = \frac{5}{{13}} \Rightarrow IE = \frac{5}{{13}}IS = \frac{{10}}{3}

    Thể tích khối cầu: V = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi {\left( {\frac{{10a}}{3}} ight)^3} = \frac{{4000\pi {a^3}}}{{81}} (đvtt).

  • Câu 21: Nhận biết

    Trong không gian Oxyz, cho mặt cầu (S):x^{2} + (y - 2)^{2} + (z + 1)^{2} = 6. Đường kính của (S) bằng

    Ta có bán kính của (S) là \sqrt{6} nên đường kính của (S) bằng 2\sqrt{6}.

  • Câu 22: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với  AB=2a, AD=a. Cạnh bên SA vuông góc với đáy và góc giữa SC với đáy bằng 45^0 . Gọi N là trung điểm SA, h là chiều cao của khối chóp S.ABCD và R là bán kính mặt cầu ngoại tiếp khối chóp N.ABC. Biểu thức liên hệ giữa R và h là:

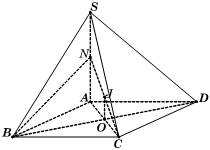
    Tìm biểu thức liên hệ

    Ta có {45^0} = \widehat {SC,\left( {ABCD} ight)} = \widehat {SC,AC} = \widehat {SCA} .

    Trong \Delta SAC, ta có h = SA = a\sqrt 5

    Ta có \left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} ight. \Rightarrow BC \bot \left( {SAB} ight) \Rightarrow BC \bot BN.

    Mặt khác, ta lại có NA \bot AC.

    Do đó hai điểm A, B cùng nhìn đoạn dưới một góc vuông nên hình chóp N.ABC nội tiếp mặt cầu tâm J là trung điểm NC, bán kính

    R = JN = \frac{{NC}}{2} = \frac{1}{2}.\sqrt {A{C^2} + {{\left( {\frac{{SA}}{2}} ight)}^2}} = \frac{{5a}}{4}.

  • Câu 23: Thông hiểu

    Cho hình nón có đỉnh S, đường cao SO = h, đường sinh SA. Nội tiếp hình nón là một hình chóp đỉnh S, đáy là hình vuông ABCD cạnh a. Nửa góc ở đỉnh của hình nón có tan bằng:

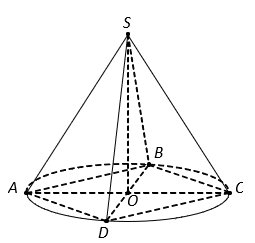
     Tính tang của góc

    Nửa góc ở đỉnh của hình nón là góc \widehat {ASO} .

    Hình vuông ABCD cạnh a nên suy ra: OA = \frac{{a\sqrt 2 }}{2}

    Trong tam giác vuông SOA, ta có \tan \widehat {ASO} = \frac{{OA}}{{SO}} = \frac{{a\sqrt 2 }}{{2h}}.

  • Câu 24: Nhận biết

    Hình nón có đường sinh l=2a và hợp với đáy góc \alpha = {60^0}. Diện tích toàn phần của hình nón bằng:

    Diện tích toàn phần

    Theo giả thiết, ta có

    SA = \ell = 2a và \widehat {SAO} = {60^0}.

    Suy ra:

    R = OA = SA.\cos {60^0} = a.

    Vậy diện tích toàn phần của hình nón bằng: S = \pi Rl + \pi {R^2} = 3\pi {a^2} (đvdt). 

  • Câu 25: Thông hiểu

    Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng R\sqrt 3. Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng 30^0. Khoảng cách giữa AB và trục của hình trụ bằng:

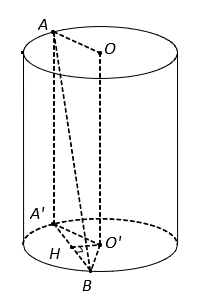
    Tính khoảng cách

    Từ hình vẽ kết hợp với giả thiết, ta có OA = O'B = R.

    Gọi AA’ là đường sinh của hình trụ thì O'A' = R,{m{ }}AA' = R\sqrt 3 và \widehat {BAA'} = {30^0}.

    Vì OO'\parallel \left( {ABA'} ight) nên d\left[ {OO',\left( {AB} ight)} ight] = d\left[ {OO',\left( {ABA'} ight)} ight] = d\left[ {O',\left( {ABA'} ight)} ight].

    Gọi H là trung điểm A’B, suy ra \left. \begin{array}{l}O'H \bot A'B\\O'H \bot AA'\end{array} ight\} \Rightarrow O'H \bot \left( {ABA'} ight)

    nên O'H = \frac{{R\sqrt 3 }}{2}h.

    Tam giác ABA’ vuông tại A’ nên BA' = AA'\tan {30^0} = R

    Suy ra tam giác A’BO đều có cạnh bằng R nên O'H = \frac{{R\sqrt 3 }}{2}.h

  • Câu 26: Thông hiểu

    Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P):x + \sqrt{2}y - z + 3 = 0 cắt mặt cầu (S):x^{2} + y^{2} + z^{2} = 5 theo giao tuyến là đường tròn có diện tích là:

    Mặt cầu (S) có tâm O(0;0;0) và bán kính R = \sqrt{5}

    Khoảng cách từ O đến (P): d\left( O;(P) ight) = \frac{3}{2}

    Bán kính đường tròn giao tuyến

    r = \sqrt{R^{2} - \left\lbrack d\left( O;(P) ight) ightbrack^{2}} = \sqrt{5 - \frac{9}{4}} = \sqrt{\frac{11}{4}}

    Diện tích đường tròn giao tuyến S = 2\pi r^{2} = \frac{11\pi}{4}.

  • Câu 27: Thông hiểu

    Cho hình trụ có chiều cao bằng 8a . Biết hai điểm A và C lần lượt nằm trên hai đáy thỏa mãn AC=10a, khoảng cách giữa AC và trục của hình trụ bằng 4a. Thể tích của khối trụ đã cho là:

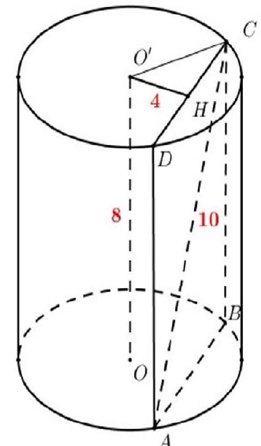
      Thể tích của khối trụ

    Gọi (O) và (O') lần lượt là hai đường tròn đáy; A\in (O), C \in (O') .

    Dựng AD, CB lần lượt song song với OO' (D \in (O'), B \in (O). Dễ dàng có ABCD là hình chữ nhật.

    Do AC=10a,AD=8a\Rightarrow DC=6a..

    Gọi H là trung điểm của DC.

    \left\{\begin{matrix}O^\prime H\bot D C\\O^\prime H\bot A D\\\end{matrix}\Rightarrow O^\prime H\bot(ABCD)ight..

    Ta có O^\prime//(ABCD)\Rightarrow d\left(OO^\prime,ACight)=d\left(OO^\prime,(ABCD)ight)=O^\prime H=4a..

    Suy ra O^\prime H=4a,CH=3a\Rightarrow R=O^\prime C=5a..

    Vậy thể tích của khối trụ là V=\pi R^2h=\pi(5a)^28a=200\pi a^3.

  • Câu 28: Vận dụng

    Cho hình nón tròn xoay có chiều cao bằng 2a, bán kính đáy bằng 3a. Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện bằng \frac{3a}{2}. Diện tích của thiết diện đó bằng?

    Xét hình nón đỉnh S có chiều cao SO=2a, bán kính đáy OA=3a .

    Thiết diện đi qua đỉnh của hình nón là tam giác SAB cân tại S.

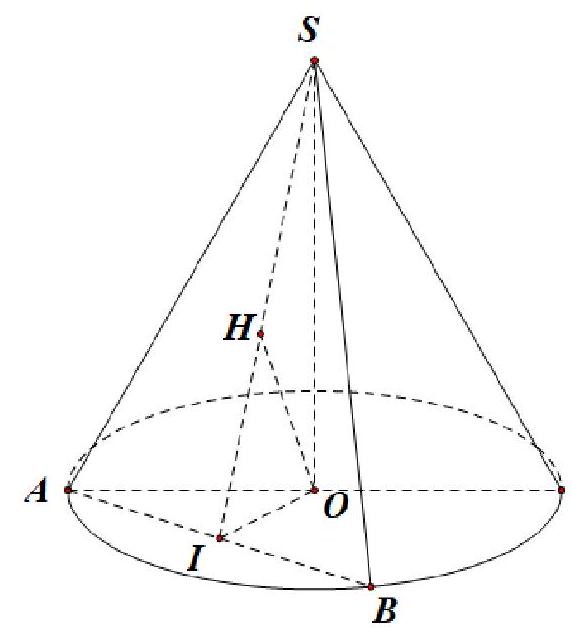
    Diện tích thiết diện

    Gọi I là trung điểm của đoạn thẳng AB. Trong tam giác SOI, kẻ OH\bot SI,H\in SI

    Ta có: 

     +\left\{\begin{matrix}AB\bot O I\\AB\bot S O\\\end{matrix}\Rightarrow A B\bot(SOI)\Rightarrow A B\bot O Hight.

    +\left\{\begin{matrix}OH\bot S I\\OH\bot A B\\\end{matrix}\Rightarrow O H\bot(SAB)\Rightarrow d(O,(SAB))=OH=\frac{3a}{2}ight.

    Xét tam giác SOI vuông tại O, ta có

    \frac{1}{OI^2}=\frac{1}{OH^2}-\frac{1}{SO^2}=\frac{4}{9a^2}-\frac{1}{4a^2}=\frac{7}{36a^2}\Rightarrow OI=\frac{6a}{\sqrt7}.

    SI=\sqrt{SO^2+OI^2}=\sqrt{4a^2+\frac{36a^2}{7}}=\frac{8a}{\sqrt7}.

    Xét tam giác AOI vuông tại I, có: 

    AI=\sqrt{AO^2-OI^2}=\sqrt{9a^2-\frac{36a^2}{7}}=\frac{3\sqrt3a}{\sqrt7}

    \Rightarrow AB=2AI=\frac{6\sqrt3a}{\sqrt7}

    Vậy diện tích của thiết diện là:

    S_{\triangle S A B}=\frac{1}{2}\cdot SI\cdot AB=\frac{1}{2}\cdot\frac{8a}{\sqrt7}\cdot\frac{6\sqrt3a}{\sqrt7}=\frac{24a^2\sqrt3}{7}.

  • Câu 29: Thông hiểu

    Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):(x - 1)^{2} + (y - 2)^{2} + (z + 1)^{2} = 25. Đường thẳng d cắt mặt cầu (S) tại hai điểm A, B. Biết tiếp diện của (S) tại A, B vuông góc. Tính độ dài AB.

    Hình vẽ minh họa

    Mặt cầu (S) có tâm I(1; 2; −1), bán kính R = 5. Xét mặt phẳng (P) chứa d cắt giao tuyến của hai tiếp diện tại O.

    Ta có tứ giác OIAB là hình vuông.

    Suy ra AB = IA.\sqrt{2} = R\sqrt{2} = 5\sqrt{2}.

  • Câu 30: Vận dụng

    Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x - 2y + 2z - 3 = 0 và mặt cầu (S) tâm I(5; - 3;5), bán kính R = 2\sqrt{5}. Từ một điểm A thuộc mặt phẳng (P) kẻ một đường thẳng tiếp xúc với mặt cầu (S) tại B. Tính OA biết AB = 4.

    Hình vẽ minh họa

    Khoảng cách từ điểm I đến mặt phẳng (P) là

    d\left( I;(P) ight) = \frac{\left| 5 - 2.( - 3) + 2.5 - 3 ight|}{3} = 6

    Vì AB tiếp xúc với (S) tại B nên tam giác AIB vuông tại B, do đó ta có:

    IA = \sqrt{IB^{2} + AB^{2}} = \sqrt{R^{2} + AB^{2}} = 6 = d\left( I;(P) ight)

    Đường thẳng IA đi qua I(5; −3; 5) có vectơ chỉ phương là \overrightarrow{u} = (1; - 2;2) nên có phương trình là: \left\{ \begin{matrix} x = 5 + t \\ y = - 3 - 2t \\ z = 5 + 2t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)

    Do A = IA ∩ (P) nên 5 + t − 2(−3 − 2t) + 2(5 + 2t) − 3 = 0 ⇔ t = −2

    Vậy A(3; 1; 1) nên OA = \sqrt{11}.

  • Câu 31: Thông hiểu

    Cho mặt cầu \left( S ight):{x^2} + {y^2} + {z^2} + 4x - 2y + 6z - 2 = 0 và mặt phẳng \left( P ight):3x + 2y + 6z + 1 = 0. Gọi (C) là đường tròn giao tuyến của (P) và (S). Tính tọa độ tâm H của (C).

     Theo đề bài, mặt cầu (S) có tâm I\left( { - 2,1, - 3} ight) và vecto pháp tuyến của (P):\,\,\overrightarrow n = \left( {3,2,6} ight)

    \begin{array}{l}IH \bot \left( P ight) \Rightarrow IH:x = - 2 + 3t;\,\,y = 1 + 2t;\,\,z = - 3 + 6t\\H \in \left( P ight) \Rightarrow 3\left( { - 2 + 3t} ight) + 2\left( {1 + 2t} ight) + 6\left( { - 3 + 6t} ight) + 1 = 0 \Leftrightarrow t = \dfrac{3}{7}\\ \Rightarrow H\left( { - \dfrac{5}{7},\dfrac{{13}}{7}, - \dfrac{3}{7}} ight)\end{array}

  • Câu 32: Thông hiểu

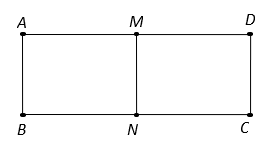
    Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2 . Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ. Diện tích toàn phần của hình trụ bằng:

    Diện tích toàn phần

    Theo giả thiết ta được hình trụ có chiều cao h=AB=1 , bán kính đáy R = \frac{{AD}}{2} = 1

    Do đó diện tích toàn phần: {S_{tp}} = 2\pi Rh + 2\pi {R^2} = 4\pi

  • Câu 33: Thông hiểu

    Bán kính đáy hình trụ bằng 4 cm, chiều cao bằng 6cm. Độ dài đường chéo của thiết diện qua trục bằng:

     Thiết diện qua trục của một hình trụ là một hình chữ nhật có hai cạnh lần lượt bằng đường kính đáy và chiều cao của hình trụ.

    Vậy hai cạnh của hình chữ nhật là 8 cm và 6 cm.

    Do đó độ đài đường chéo: \sqrt {{8^2} + {6^2}} = 10{m{cm}}{m{.}}

  • Câu 34: Thông hiểu

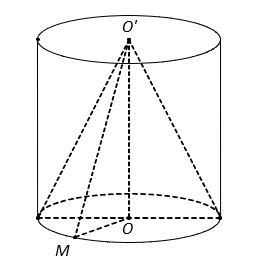
    Cho hình trụ có hai đáy là hai hình tròn (O) và (O’), chiều cao R\sqrt 3 và bán kính đáy R. Một hình nón có đỉnh là O’ và đáy là hình tròn (O;R). Tỉ số diện tích xung quanh của hình trụ và hình nón bằng:

    Tỉ số diện tích

    Diện tích xung quanh của hình trụ:

    {S_{{m{xq}}\left( {m{T}} ight)}} = 2\pi R.h = 2\pi R.R\sqrt 3 = 2\sqrt 3 \pi {R^2} (đvdt).

    Kẻ đường sinh O’M của hình nón, suy ra

    \ell = O'M = \sqrt {OO{'^2} + O{M^2}} = \sqrt {3{R^2} + {R^2}} = 2R.

    Diện tích xung quanh của hình nón: {S_{{m{xq}}\left( {m{N}} ight)}} = \pi R\ell = \pi R.2R = 2\pi {R^2} (đvdt).

    Vậy \frac{{{S_{{m{xq}}\left( {m{T}} ight)}}}}{{{S_{{m{xq}}\left( {m{N}} ight)}}}} = \sqrt 3.

  • Câu 35: Vận dụng cao

    Cho hình nón đỉnh S có đáy là hình tròn tâm O. Một mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là một tam giác vuông  SAB có diện tích bằng 4a^2. Góc giữa trục SO và mặt phẳng (SAB) bằng {30}^\circ. Diện tích xung quanh của hình nón đã cho bằng?

     

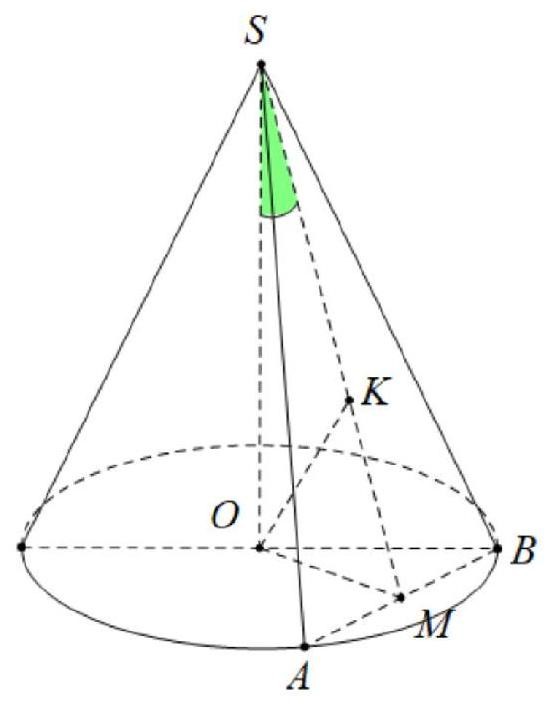
    Gọi M là trung điểm của AB , tam giác OAB cân đỉnh O nên OM\bot AB  và SO\bot AB suy ra AB\bot(SOM)

    Dựng OK\bot SM..

    Theo trên có OK\bot AB nên OK\bot(SAB).

    Vậy góc tạo bởi giữa trục SO và mặt phẳng (SAB) là \widehat{OSM}={30}^\circ. Tam giác vuông cân SAB có diện tích bằng 4a^2 suy ra \frac{1}{2}SA^2=4a^2\Rightarrow SA=2a\sqrt2

    \Rightarrow AB=4a\Rightarrow SM=2a..

    Xét tam giác vuông SOM có \cos\widehat{OSM}=\frac{SO}{SM}\Rightarrow SO=\frac{\sqrt3}{2}\cdot2a=\sqrt3a..

    Cuối cùng OB=\sqrt{SB^2-SO^2}=a\sqrt5.

    Vậy diện tích xung quanh của hình nón bằng S_{xq}=\pi rl=\pi\cdot a\sqrt5\cdot2a\sqrt2=2a^2\sqrt{10}\pi.

  • Câu 36: Thông hiểu

    Trong không gian với hệ toạ độ Oxyz, cho điểm M(1; - 2;3). Gọi I là hình chiếu vuông góc của M trên trục Ox. Phương trình nào dưới đây là phương trình mặt cầu tâm I bán kính IM?

    Hình chiếu vuông góc của M trên Ox là: I(1;0;0)

    \Rightarrow IM = \sqrt{13}

    Suy ra phương trình mặt cầu tâm I bán kính IM là: (x - 1)^{2} + y^{2} + z^{2} = 13.

  • Câu 37: Thông hiểu

    Cho hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R. Dựng hai đường sinh SA và SB, biết AB chắn trên đường tròn đáy một cung có số đo bằng 60^0, khoảng cách từ tâm O đến mặt phẳng (SAB) bằng \frac{R}{2}. Đường cao h của hình nón bằng:

    Theo giả thiết ta có tam giác OAB đều cạnh R.

    Gọi E là trung điểm AB, suy ra OE \bot AB và OE = \frac{{R\sqrt 3 }}{2}.

    Gọi H là hình chiếu của O trên SE, suy ra OH \bot SE.

    Ta có \left\{ \begin{array}{l}AB \bot OE\\AB \bot SO\end{array} ight. \Rightarrow AB \bot \left( {SOE} ight) \Rightarrow AB \bot OH

    Từ đó suy ra OH \bot \left( {SAB} ight) nên d\left[ {O,\left( {SAB} ight)} ight] = OH = \frac{R}{2}.

    Trong tam giác vuông SOE, ta có  \frac{1}{{S{O^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{O{E^2}}} = \frac{8}{{3{R^2}}} \Rightarrow SO = \frac{{R\sqrt 6 }}{4}

  • Câu 38: Vận dụng

    Trong không gian Oxyz, cho điểm A(0; 1; 2), mặt phẳng (α): x−y +z −4 = 0 và mặt cầu (S):(x - 3)^{2} + (y - 1)^{2} + (z - 2)^{2} = 16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x’Ox là

    Gọi (C) là giao tuyến của mặt phẳng (P) và mặt cầu (S) và (C) có tâm H, bán kính r.

    Bán kính r của đường tròn là nhỏ nhất khi và chỉ khi IH lớn nhất khi và chỉ khi d(I,(P)) lớn nhất.

    Vì M ∈ x'Ox nên gọi M(m; 0; 0).

    Suy ra mặt phẳng (P) chứa AM và (P) ⊥ (α).

    Khi đó \overrightarrow{n_{(P)}} = \left\lbrack \overrightarrow{MA};\overrightarrow{n_{(\alpha)}} ightbrack = (3;2 + m;m - 1)

    Mà mặt phẳng (P) đi qua A nên phương trình của mặt phẳng (P) là:

    3(x − 0) + (2 + m)(y − 2) + (m − 1)(z − 2) = 0 hay 3x + (2 + m)y + (m − 1)z −3m=0

    Ta có:

    d\left( I;(P) ight) = \frac{9}{\sqrt{2m^{2} + 2m + 14}} lớn nhất khi và chỉ khi 2m^{2} + 2m + 14 đạt giá trị nhỏ nhất

    Mà 2m^{2} + 2m + 14 = 2\left( m + \frac{1}{2} ight)^{2} + \frac{27}{2} \geq \frac{27}{2}

    Do đó 2m^{2} + 2m + 14 nhỏ nhất khi và chỉ khi m = - \frac{1}{2}

    Vậy M\left( - \frac{1}{2};0;0 ight).

  • Câu 39: Nhận biết

    Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S):x^{2} + y^{2} + z^{2} - 2y + 2z - 7 = 0. Bán kính của mặt cầu (S) là:

    Ta có:

    x^{2} + y^{2} + z^{2} - 2y + 2z - 7 = 0

    \Leftrightarrow x^{2} + y^{2} + z^{2} - 2.0.x - 2.1y - 2.( - 1)z - 7 = 0

    \Leftrightarrow \left\{ \begin{matrix} a = 0 \\ b = 1 \\ c = - 1 \\ d = - 7 \\ \end{matrix} ight. suy ra tâm mặt cầu là: I(0;1; - 1)

    Bán kính mặt cầu là:

    R = \sqrt{a^{2} + b^{2} + c^{2} - d} = \sqrt{0^{2} + 1^{2} + ( - 1)^{2} - 7} = 3

  • Câu 40: Nhận biết

    Cho đường tròn (C) đường kính AB và đường thẳng \triangle. Để hình tròn xoay sinh bởi (C) khi quay quanh \triangle là một mặt cầu thì cần có thêm điều kiện nào sau đây:

    Điều kiện để hình tròn xoay sinh bởi (C) khi quay quanh \triangle là một mặt cầu là trục quay \triangle phải cố định và hai điểm A, B cũng cố định trên \triangle.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 2 Mặt nón, mặt trụ, mặt cầu Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 3 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 45 phút Chương 2 Mặt nón, mặt trụ, mặt cầu
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập