Lớp 10 Toán 10 - Chân trời sáng tạo

Đề kiểm tra 45 phút Chương 4 Hệ thức lượng trong tam giác Sách CTST

Mô tả thêm: Đề kiểm tra 1 tiết Toán 10 Hệ thức lượng trong tam giác gồm 40 câu hỏi trắc nghiệm giúp bạn học ôn tập, củng cố lại kiến thức sách Chân trời sáng tạo.
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Nhận biết

    Tam giác ABC có AB = 2,\ \ AC = 1 và \widehat{A} = 60{^\circ}. Tính độ dài cạnh BC.

    Theo định lí hàm cosin, ta có BC^{2} = AB^{2} + AC^{2} - 2AB.AC.cos\widehat{A} = 2^{2} + 1^{2} - 2.2.1.cos60{^\circ} = 3 \Rightarrow BC = \sqrt{3}.

  • Câu 2: Thông hiểu

    Tam giác ABC có AB = \sqrt{2},\ \ AC = \sqrt{3} và \widehat{C} = 45{^\circ}. Tính độ dài cạnh BC.

    Theo định lí hàm cosin, ta có

    AB^{2} = AC^{2} + BC^{2} - 2.AC.BC.cos\widehat{C}

    \Rightarrow \left( \sqrt{2} ight)^{2} = \left( \sqrt{3} ight)^{2} + BC^{2} - 2.\sqrt{3}.BC.cos45{^\circ}

    \Rightarrow BC = \frac{\sqrt{6} + \sqrt{2}}{2}.

  • Câu 3: Vận dụng

    Tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E,\ \ F sao cho các góc \widehat{MPE},\ \ \widehat{EPF},\ \ \widehat{FPQ} bằng nhau. Đặt MP = q,\ \ PQ = m,\ \ PE = x,\ \ PF = y. Trong các hệ thức sau, hệ thức nào đúng?

    Ta có \widehat{MPE} = \widehat{EPF} = \widehat{FPQ} = \frac{\widehat{MPQ}}{3} = 30{^\circ} \Rightarrow \widehat{MPF} = \widehat{EPQ} = 60{^\circ}.

    Theo định lí hàm cosin, ta có

    ME^{2} = AM^{2} + AE^{2} - 2.AM.AE.cos\widehat{MAE}

    = q^{2} + x^{2} - 2qx.cos30{^\circ} = q^{2} + x^{2} - qx\sqrt{3}

    MF^{2} = AM^{2} + AF^{2} - 2AM.AF.cos\widehat{MAF}

    = q^{2} + y^{2} - 2qy.cos60{^\circ} = q^{2} + y^{2} - qy

    MQ^{2} = MP^{2} + PQ^{2} = q^{2} + m^{2}.

  • Câu 4: Nhận biết

    Tam giác ABC có BC = 10 và \widehat{A}=30°. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

     Ta có: \frac {BC}{\sin A}=2R \Leftrightarrow R= \frac{BC}{2\sin A} =\frac {10}{2.sin30^{\circ} }=10.

  • Câu 5: Thông hiểu

    Cho \sin\alpha =\frac{1}{4}, với 0^{\circ} < \alpha < 90^{\circ}. Giá trị \cos\alpha bằng

    Ta có:

    \cos^{2}\alpha = 1 -\sin^{2}\alpha

    = 1 - \left( \frac{1}{4} ight)^{2} = \frac{15}{16}

    \Rightarrow \cos\alpha =\frac{\sqrt{15}}{4} (do 0^{\circ} < \alpha < 90^{\circ}).

    Vậy \cos\alpha =\frac{\sqrt{15}}{4}.

  • Câu 6: Nhận biết

    Cho \Delta ABC thỏa mãn : 2cosB = \sqrt{2}. Khi đó:

    Ta có: 2cosB = \sqrt{2} \Leftrightarrow \cos B = \frac{\sqrt{2}}{2} \Rightarrow \widehat{B} = 45^{0}.

  • Câu 7: Nhận biết

    Cho tam giác ABC có a = 8,b = 10, góc C bằng 60^{0} . Độ dài cạnh c là ?

    Ta có: c^{2} = a^{2} + b^{2} - 2a.b.cosC = 8^{2} + 10^{2} - 2.8.10.cos60^{0} = 84 \Rightarrow c = 2\sqrt{21}.

  • Câu 8: Nhận biết

    Cho \Delta ABC có a = 4,c = 5,B = 150^{0}. Diện tích của tam giác là:

    Ta có: S_{\Delta ABC} = \frac{1}{2}a.c.sinB = \frac{1}{2}.4.5.sin150^{0} = 5.

  • Câu 9: Vận dụng

    Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội – Huế), người ta cắm hai cọc AM và BN cao 1,5 mét so với mặt đất. Hai cọc này song song và cách nhau 10 mét và thẳng hàng so với tim cột cờ (Hình vẽ minh họa). Đặt giác kế tại đỉnh A và B để nhắm đến đỉnh cột cờ, người ta được các góc lần lượt là 51°40' và 45°39' so với đường song song mặt đất.

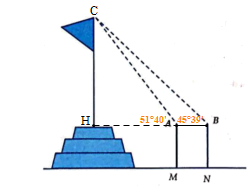
    Tính chiều cao của cột cờ

    Chiều cao của cột cờ (làm tròn kết quả đến chữ số thập phân thứ hai) là:

    Ta có: \widehat {CAB} = {180^0} - {51^0}40' = {128^0}20'

    Xét tam giác ABC ta có:

    \begin{matrix} \widehat {ABC} + \widehat {CAB} + \widehat {ACB} = {180^0} \hfill \\ \Leftrightarrow \widehat {ACB} = {180^0} - \left( {\widehat {ABC} + \widehat {CAB}} ight) \hfill \\ \Leftrightarrow \widehat {ACB} = {180^0} - \left( {{{45}^0}39' + {{128}^0}20'} ight) \hfill \\ \Leftrightarrow \widehat {ACB} = {6^0}1\prime \hfill \\ \end{matrix}

    Áp dụng định lí sin trong tam giác ABC ta có:

    \begin{matrix} \dfrac{{AB}}{{\sin \widehat {ACB}}} = \dfrac{{AC}}{{\sin \widehat {ABC}}} = \dfrac{{BC}}{{\sin \widehat {CAB}}} \hfill \\ \Rightarrow \dfrac{{10}}{{\sin {6^0}1'}} = \dfrac{{AC}}{{\sin {{45}^0}39'}} \hfill \\ \Rightarrow AC = \dfrac{{10.\sin {{45}^0}39'}}{{\sin {6^0}1'}} \hfill \\ \end{matrix}

    Ta có tam giác ACH vuông tại C

    \begin{matrix} \Rightarrow CH = AC.\sin \widehat {HAC} \hfill \\ \Rightarrow CH = \dfrac{{10.\sin {{45}^0}39'}}{{\sin {6^0}1'}}.\sin {51^0}40' \approx 53,51\left( m ight) \hfill \\ \end{matrix}

    Chiều cao của cột cờ khoảng: 1,5+53,51=55,01(m)

  • Câu 10: Nhận biết

    Cho biết \tan\alpha = \frac{1}{2}. Tính \cot\alpha.

    Ta có: \tan\alpha.cot\alpha = 1 \Rightarrow \cot\alpha = \frac{1}{\tan\alpha} = \frac{1}{\frac{1}{2}} = 2.

  • Câu 11: Thông hiểu

    Tam giác ABC có AB=\sqrt{2},AC=\sqrt{3} và \widehat{C}=45°. Tính độ dài cạnh BC.

     Áp dụng định lý côsin: A{B^2} = C{A^2} + C{B^2} - 2CA.CB.\cos 45^\circ\Leftrightarrow 2 = 3 + C{B^2} - 2\sqrt 3 .CB.\frac{{\sqrt 2 }}{2}\Leftrightarrow C{B^2} - \sqrt 6 CB + 1 = 0\Rightarrow BC=\frac{{\sqrt 6 + \sqrt 2 }}{2}.

     

  • Câu 12: Thông hiểu

    Nếu tam giác ABC có BC^{2} < AB^{2} + AC^{2} thì:

    Nếu tam giác ABC có BC^{2} < AB^{2} + AC^{2} thì \widehat{A} là góc nhọn

  • Câu 13: Thông hiểu

    Tam giác đều ABC có đường cao AH. Khẳng định nào sau đây là đúng?

    Hình ảnh minh họa

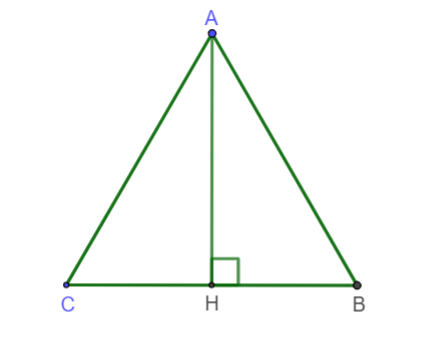
    Chọn khẳng định đúng

    Do tam giác ABC là tam giác đều có AH là đường cao nên đồng thời là đường phân giác

    => \widehat {BAH} = \frac{1}{2}\widehat {BAC}=30^0;\widehat {ABC} = {60^0};\widehat {AHC} = {90^0}

    Do đó: \sin \widehat {BAH} = \frac{1}{2};\sin \widehat {BAH} = \frac{{\sqrt 3 }}{2}

    Ta có: \widehat {ABC} = {60^0} \Rightarrow \sin \widehat {ABC} = \frac{{\sqrt 3 }}{2}

  • Câu 14: Nhận biết

    Trong các khẳng định sau, khẳng định nào là đúng?

     Ta có: \cos 121^{\circ} =\cos -121^{\circ} vì \cos \alpha =\cos -\alpha.

  • Câu 15: Nhận biết

    Cho tam giác ABC có AB = 12,AC = 13,BC = 5. Diện tích S của tam giác ABC là:

    Ta có: BA^{2} + BC^{2} = AC^{2} nên tam giác ABC vuông tại B.

    Diện tích tam giác là: S = \frac{1}{2}BA \cdot BC = 30.

  • Câu 16: Thông hiểu

    Cho hình thoi ABCD cạnh bằng 1\ \ cm và có \widehat{BAD} = 60{^\circ}. Tính độ dài cạnh AC.

    Do ABCD là hình thoi, có \widehat{BAD} = 60{^\circ} \Rightarrow \widehat{ABC} = 120{^\circ}.

    Theo định lí hàm cosin, ta có

    AC^{2} = AB^{2} + BC^{2} - 2.AB.BC.cos\widehat{ABC}

    = 1^{2} + 1^{2} - 2.1.1.cos120{^\circ} = 3 \Rightarrow AC = \sqrt{3}

  • Câu 17: Thông hiểu

    Điểm cuối của góc lượng giác \alpha ở góc phần tư thứ mấy nếu \sin\alpha,\ tan\alpha trái dấu?

    Điểm cuối của \alpha thuộc góc phần tư thứ hai thì \sin\alpha > 0, \cos\alpha < 0.

    Điểm cuối của \alpha thuộc góc phần tư thứ tư thì \sin\alpha < 0, \cos\alpha > 0.

    Vậy nếu \sin\alpha,\ cos\alpha trái dấu thì điểm cuối của góc lượng giác \alpha ở góc phần tư thứ II hoặc IV.

  • Câu 18: Vận dụng cao

    Cho tam giác ABC thỏa mãn biểu thức

    \sin\dfrac{\widehat{B}}{2}.\cos^{3}\dfrac{\widehat{C}}{2}= \sin\frac{\widehat{C}}{2}.\cos^{3}\dfrac{\widehat{B}}{2}

    Khi đó tam giác ABC là tam giác gì?

    Ta có:

    \sin\dfrac{\widehat{B}}{2}.\cos^{3}\dfrac{\widehat{C}}{2}= \sin\dfrac{\widehat{C}}{2}.\cos^{3}\dfrac{\widehat{B}}{2}

    \Leftrightarrow\tan\dfrac{\widehat{B}}{2}.\dfrac{1}{\cos^{2}\dfrac{\widehat{B}}{2}} =\tan\dfrac{\widehat{C}}{2}.\dfrac{1}{\cos^{2}\dfrac{\widehat{C}}{2}}

    \Leftrightarrow\tan\dfrac{\widehat{B}}{2}.\left( 1 + \tan^{2}\dfrac{\widehat{B}}{2}ight) = \tan\dfrac{\widehat{C}}{2}.\left( 1 +\tan^{2}\dfrac{\widehat{C}}{2} ight)

    Đặt \tan\dfrac{\widehat{B}}{2} =x;\tan\dfrac{\widehat{C}}{2} = y khi đó ta có:

    x\left( 1 + x^{2} ight) = y\left( 1 + y^{2} ight)

    \Leftrightarrow x^{3} - y^{3} + x - y = 0

    \Leftrightarrow (x - y)\left( x^{2} + xy + y^{2} + 1 ight) = 0

    \Leftrightarrow x - y = 0

    Do đó \tan\frac{\widehat{B}}{2} = \tan\frac{\widehat{C}}{2} \Leftrightarrow \frac{\widehat{B}}{2} = \frac{\widehat{C}}{2} \Leftrightarrow \widehat{B} = \widehat{C}

    Vậy tam giác ABC là tam giác cân tại A.

  • Câu 19: Thông hiểu

    Cho tam giác ABC có b = 7; c = 5, \cos A = \frac{3}{5}. Đường cao h_{a} của tam giác ABC là:

    Ta có: a^{2} = b^{2} + c^{2} - 2bc\cos A = 7^{2} + 5^{2} - 2.7.5.\frac{3}{5} = 32 \Rightarrow a = 4\sqrt{2}.

    Mặt khác: sin^{2}A + cos^{2}A = 1 \Rightarrow sin^{2}A = 1 - cos^{2}A = 1 - \frac{9}{25} = \frac{16}{25} \Rightarrow \sin A = \frac{4}{5} (Vì \sin A > 0).

    Mà: S_{\Delta ABC} = \frac{1}{2}b.c.sinA = \frac{1}{2}a.h_{a} \Rightarrow h_{a} = \frac{bc\sin A}{a} = \frac{7.5.\frac{4}{5}}{4\sqrt{2}} = \frac{7\sqrt{2}}{2}.

  • Câu 20: Vận dụng

    Cho góc \alpha thỏa mãn \frac{\pi}{2} < \alpha < 2\pi và \tan\left( \alpha + \frac{\pi}{4} ight) = 1. Tính P = \cos\left( \alpha - \frac{\pi}{6} ight) + \sin\alpha.

    Ta có \left\{ \begin{matrix} \frac{\pi}{2} < \alpha < 2\pi\overset{}{\leftrightarrow}\frac{3\pi}{4} < \alpha + \frac{\pi}{4} < \frac{9\pi}{4} \\ \tan\left( \alpha + \frac{\pi}{4} ight) = 1 \\ \end{matrix} ight.

    ightarrow \alpha + \frac{\pi}{4} = \frac{5\pi}{4} ightarrow\alpha = \pi.

    Thay \alpha = \pi vào P, ta được P = - \frac{\sqrt{3}}{2}.

  • Câu 21: Vận dụng cao

    Cho biểu thức B xác định, rút gọn biểu thức

    B = \sqrt{2} - \frac{1}{\sin(x + 2013\pi)}.\sqrt{\frac{1}{1 + \cos x} + \frac{1}{1 - \cos x}} với \pi < x < 2\pi?

    Ta có:

    \sin(x + 2013\pi) = \sin(x + \pi + 2012\pi) = \sin(x + \pi) = - \sin x

    Do đó:

    B = \sqrt{2} - \frac{1}{\sin(x + 2013\pi)}.\sqrt{\frac{1}{1 + \cos x} + \frac{1}{1 - \cos x}}

    B = \sqrt{2} + \frac{1}{\sin x}.\sqrt{\frac{1 - \cos x + 1 + \cos x}{\left( 1 + \cos x ight)\left( 1 - \cos x ight)}}

    B = \sqrt{2} + \dfrac{1}{\sin x}.\sqrt{\dfrac{2}{1 - \cos^{2}x}}

    B = \sqrt{2} + \frac{1}{\sin x}.\sqrt{\dfrac{2}{\sin^{2}x}}

    B = \sqrt{2}\left( 1 + \frac{1}{\sin x.\left| \sin x ight|} ight)

    Vì \pi < x < 2\pi nên \sin x < 0

    \Rightarrow B = \sqrt{2}\left( 1 -\dfrac{1}{\sin^{2}x} ight) = - \sqrt{2}\cot^{2}x

  • Câu 22: Nhận biết

    Điểm cuối của \alpha thuộc góc phần tư thứ tư của đường tròn lượng giác. Khẳng định nào sau đây là đúng?

    Điểm cuối của \alpha thuộc góc phần tư thứ hai ightarrow \left\{ \begin{matrix} \sin\alpha < 0 \\ \cos\alpha > 0 \\ \tan\alpha < 0 \\ \cot\alpha < 0 \\ \end{matrix} ight..

  • Câu 23: Thông hiểu

    Cho \cos\alpha = \frac{4}{5} với 0 < \alpha < \frac{\pi}{2}. Tính \sin\alpha.

    Ta có: sin^{2}\alpha = 1 - cos^{2}\alpha = 1 - \left( \frac{4}{5} ight)^{2} = \frac{9}{25} \Rightarrow \sin\alpha = \pm \frac{3}{5}.

    Do 0 < \alpha < \frac{\pi}{2} nên \sin\alpha > 0. Suy ra, \sin\alpha = \frac{3}{5}

  • Câu 24: Vận dụng

    Cho góc \alpha thỏa mãn 3cos\alpha + 2sin\alpha = 2 và \sin\alpha < 0. Tính \sin\alpha.

    Ta có 3cos\alpha + 2sin\alpha = 2 \Leftrightarrow (3cos\alpha + 2sin\alpha)^{2} = 4

    \begin{matrix} \Leftrightarrow 9cos^{2}\alpha + 12cos\alpha.sin\alpha + 4sin^{2}\alpha = 4 \\ \\ \end{matrix} \Leftrightarrow 5cos^{2}\alpha + 12cos\alpha.sin\alpha = 0

    \Leftrightarrow \cos\alpha(5cos\alpha + 12sin\alpha) = 0 \Leftrightarrow \left\lbrack \begin{matrix} \cos\alpha = 0 \\ 5cos\alpha + 12sin\alpha = 0 \\ \end{matrix} ight.\ .

    \bullet \cos\alpha = 0 \Rightarrow \sin\alpha = 1: loại (vì \sin\alpha < 0).

    \bullet 5cos\alpha + 12sin\alpha = 0, ta có hệ phương trình \left\{ \begin{matrix} 5cos\alpha + 12sin\alpha = 0 \\ 3cos\alpha + 2sin\alpha = 2 \\ \end{matrix} ight. \Leftrightarrow \left\{ \begin{matrix} \sin\alpha = - \frac{5}{13} \\ \cos\alpha = \frac{12}{13} \\ \end{matrix} ight.\ .

  • Câu 25: Nhận biết

    Giá trị cot\frac{\pi }{6} là:

     Ta có: cot\frac{\pi }{6} =\sqrt3.

  • Câu 26: Thông hiểu

    Cho tam giác ABC, chọn công thức đúng trong các đáp án sau:

    Ta có: m_{a}^{2} = \frac{b^{2} + c^{2}}{2} - \frac{a^{2}}{4} = \frac{2b^{2} + 2c^{2} - a^{2}}{4}.

  • Câu 27: Nhận biết

    Tam giác ABC có \widehat{B} = 60^{\circ},\widehat{C} = 45^{\circ} và AB = 5. Tính độ dài cạnh AC.

    Theo định lí sin ta có:

    \frac{AB}{\sin C} = \frac{AC}{\sin B} \Leftrightarrow \frac{5}{\sin 45^{\circ}} = \frac{AC}{\sin 60^{\circ}}

    \Leftrightarrow AC = \frac{5\sqrt{6}}{2}.

  • Câu 28: Vận dụng

    Cho góc \alpha thỏa mãn 0 < \alpha < \frac{\pi}{4} và \sin\alpha + \cos\alpha = \frac{\sqrt{5}}{2}. Tính P = \sin\alpha - \cos\alpha.

    Ta có \left( \sin\alpha - \cos\alpha ight)^{2} + \left( \sin\alpha + \cos\alpha ight)^{2} = 2\left( sin^{2}\alpha + cos^{2}\alpha ight) = 2.

    Suy ra \left( \sin\alpha - \cos\alpha ight)^{2} = 2 - \left( \sin\alpha + \cos\alpha ight)^{2} = 2 - \frac{5}{4} = \frac{3}{4}.

    Do 0 < \alpha < \frac{\pi}{4} suy ra \sin\alpha < \cos\alpha nên \sin\alpha - \cos\alpha < 0. Vậy P = - \frac{\sqrt{3}}{2}.

  • Câu 29: Nhận biết

    Cho tam giác ABC có a=2,\hat A=60^{\circ} ,\hat B=45^{\circ}. Hỏi độ dài cạnh b bằng bao nhiêu?

     Áp dụng định lí sin:

    \frac{a}{{\sin A}} = \frac{b}{{\sin B}} \Leftrightarrow b = \sin B.\frac{a}{{\sin A}}= \sin 45^\circ .\frac{2}{{\sin 60^\circ }} = \frac{{2\sqrt 6 }}{3}.

  • Câu 30: Thông hiểu

    Cho tam giác ABC, biết BC = 24, AC = 13, AB = 15. Số đo góc A là:

    Áp dụng hệ quả định lí cosin cho tam giác ABC ta có:

    \begin{matrix} \cos \widehat A = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} \hfill \\ \Rightarrow \cos \widehat A = \dfrac{{{{15}^2} + {{13}^2} - {{24}^2}}}{{2.15.13}} = - \dfrac{7}{{15}} \hfill \\ \Rightarrow \widehat A \approx {117^0}49\prime \hfill \\ \end{matrix}

  • Câu 31: Nhận biết

    Cho 2\pi < \alpha < \frac{5\pi}{2}. Khẳng định nào sau đây đúng?

    Ta có 2\pi < \alpha < \frac{5\pi}{2}\overset{}{ightarrow}điểm cuối cung \alpha - \pi thuộc góc phần tư thứ I\overset{}{ightarrow}\left\{ \begin{matrix} \tan\alpha > 0 \\ \cot\alpha > 0 \\ \end{matrix} ight.\ .

  • Câu 32: Nhận biết

    Tam giác ABC có AB=5,BC=7,CA=8. Số đo góc \hat A bằng:

     Áp dụng định lí côsin:

    \cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}}= \frac{{{5^2} + {8^2} - {7^2}}}{{2.5.8}} = \frac{1}{2}.

    Suy ra \hat A = 60^{\circ}.

  • Câu 33: Thông hiểu

    Điểm cuối của góc lượng giác \alpha ở góc phần tư thứ mấy nếu \sqrt{sin^{2}}\alpha = \sin\alpha.

    Ta có \sqrt{sin^{2}\alpha} \Leftrightarrow \sin\alpha \Leftrightarrow \left| \sin\alpha ight| = \sin\alpha.

    Đẳng thức \left| \sin\alpha ight| = \sin\alpha\overset{}{ightarrow}\sin\alpha \geq 0\overset{}{ightarrow}điểm cuối của góc lượng giác \alpha ở góc phần tư thứ I hoặc II.

  • Câu 34: Thông hiểu

    Cho góc \alpha thỏa mãn \sin\alpha = \frac{12}{13} và \frac{\pi}{2} < \alpha < \pi. Tính \cos\alpha.

    Ta có: \left\{ \begin{matrix} \cos\alpha = \pm \sqrt{1 - sin^{2}\alpha} = \pm \frac{5}{13} \\ \frac{\pi}{2} < \alpha < \pi \\ \end{matrix} ight. \overset{}{ightarrow}\cos\alpha = - \frac{5}{13}.

  • Câu 35: Nhận biết

    Tam giác ABC có AB = 5,\ \ BC = 7,\ \ CA = 8. Số đo góc \widehat{A} bằng:

    Theo định lí hàm cosin, ta có \cos\widehat{A} = \frac{AB^{2} + AC^{2} - BC^{2}}{2AB.AC} = \frac{5^{2} + 8^{2} - 7^{2}}{2.5.8} = \frac{1}{2}.

    Do đó, \widehat{A} = 60{^\circ}.

  • Câu 36: Nhận biết

    Tam giác ABC có \hat B = {60^0},\hat C = {45^0};AC = 5. Độ dài cạnh AB là:

    Áp dụng định lí sin trong tam giác ABC ta có:

    \begin{matrix} \dfrac{{AC}}{{\sin B}} = \dfrac{{AB}}{{\sin C}} \hfill \\ \Rightarrow AB = \dfrac{{AC.\sin C}}{{\sin B}} = \dfrac{{5.\sin {{45}^0}}}{{\sin {{60}^0}}} = \dfrac{{5\sqrt 6 }}{3} \hfill \\ \end{matrix}

  • Câu 37: Nhận biết

    Cho tam giác ABC có AB=1;AC=\sqrt2;\hat A=45^{\circ}. Tính độ dài cạnh BC.

     Áp dụng định lí côsin:

    BC^2=AB^2+AC^2-2.AB.AC.\cos A=1+2-2.1.\sqrt2.\cos45^{\circ} =1.

    Suy ra BC=1.

  • Câu 38: Vận dụng cao

    Cho tam giác ABC có các góc thỏa mãn biểu thức

    \sin^{2}\widehat{A} + \sin^{2}\widehat{B}= \sqrt[2017]{\sin\widehat{C}}

    Giả sử AB = c;BC = a;AC = b. Tính số đo góc \widehat{C}?

    Ta có:

    \sin\widehat{C} \in \lbrack - 1;1brack \Rightarrow sin^{2017}\widehat{C} \geq sin^{2}\widehat{C}

    \Rightarrow sin^{2}\widehat{A} + sin^{2}\widehat{B} \geq sin^{2}\widehat{C}

    \Rightarrow 4R^{2}.\left\lbrack sin^{2}\widehat{A} + sin^{2}\widehat{B} ightbrack \geq 4R^{2}.sin^{2}\widehat{C}

    \Rightarrow a^{2} + b^{2} \geq c^{2}

    \Rightarrow a^{2} + b^{2} - c^{2} \geq 0

    Theo định lí cosin ta có:

    \Rightarrow \cos\widehat{C} = \frac{a^{2} + b^{2} - c^{2}}{2ab} \geq 0

    Ta thấy

    \sin^{2}\widehat{A} + \sin^{2}\widehat{B}= \frac{1 - \cos2\widehat{A}}{2} + \frac{1 -\cos2\widehat{B}}{2}

    = 1 - \frac{\cos2\widehat{A} +\cos2\widehat{B}}{2}

    = 1 - \cos\left( \widehat{A} +\widehat{B} ight).\cos\left( \widehat{A} - \widehat{B}ight)

    = 1 - \cos\widehat{C}.\cos\left(\widehat{A} - \widehat{B} ight) \geq 1

    Mặt khác \sqrt[2017]{\sin\widehat{C}}\leq \sqrt[2017]{1} = 1

    Do đó: sin^{2}\widehat{A} + sin^{2}\widehat{B} = \sqrt[2017]{\sin\widehat{C}} khi \left\{ \begin{matrix}\cos\widehat{C}.\cos\left( \widehat{A} - \widehat{B} ight) = 0 \\\sin\widehat{C} = 1 \\\end{matrix} ight.

    \Rightarrow \widehat{C} =\dfrac{\pi}{2}

    Vậy tam giác ABC là tam giác vuông tại \widehat{C}.

  • Câu 39: Thông hiểu

    Cho tam giác ABC thỏa mãn BC^{2} + AC^{2} - AB^{2} - \sqrt{2}BC.AC = 0. Khi đó, góc C có số đo là:

    Theo đề bài ra ta có:

    BC^{2} + AC^{2} - AB^{2} - \sqrt{2}BC.AC = 0

    \Leftrightarrow BC^{2} + AC^{2} - AB^{2} = \sqrt{2}BC.AC

    \Leftrightarrow \frac{BC^{2} + AC^{2} - AB^{2}}{BC \cdot AC} = \sqrt{2}

    \Leftrightarrow 2\cos C - \sqrt{2} = 0

    \Leftrightarrow \cos C = \frac{\sqrt{2}}{2}\Rightarrow \widehat{C} = 45^{\circ}.

  • Câu 40: Nhận biết

    Cho tam giác ABC có AB = 8 cm, AC = 18 cm và có diện tích bằng 64 cm^{2}. Giá trị sin A là:

    Ta có: 

    \begin{matrix} {S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \widehat A \hfill \\ \Rightarrow \sin \widehat A = \dfrac{{2S}}{{AB.AC}} = \dfrac{{2.64}}{{8.18}} = \dfrac{8}{9} \hfill \\ \end{matrix}

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Chương 4 Hệ thức lượng trong tam giác Sách CTST Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Làm lại
  • 7 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 45 phút Chương 4 Hệ thức lượng trong tam giác Sách CTST
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập