Cho tam giác đều ABC có cạnh a. Tính tích vô hướng ![]()
Ta có: Tam giác ABC đều =>
Đề kiểm tra 45 phút Toán 10 Chương 4 Vectơ sách Kết nối tri thức giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!
Cho tam giác đều ABC có cạnh a. Tính tích vô hướng ![]()
Ta có: Tam giác ABC đều =>
Tổng ![]() bằng vectơ nào sau đây?
bằng vectơ nào sau đây?
Ta có
.
Trong hệ tọa độ ![]() , cho các điểm
, cho các điểm ![]() . Xác định tọa độ điểm
. Xác định tọa độ điểm ![]() thỏa mãn biểu thức
thỏa mãn biểu thức ![]() ?
?
Theo bài ra ta có:
Cho tam giác ![]() Hai điểm
Hai điểm ![]() chia cạnh
chia cạnh ![]() theo ba phần bằng nhau
theo ba phần bằng nhau ![]() Tính
Tính ![]() theo
theo ![]() và
và ![]()
Ta có
Cho hình bình hành ABCD. Với mọi điểm M, ta có khẳng định nào sau đây:
Ta có: (Đúng).
Cho lục giác đều ![]() có tâm
có tâm ![]() Đẳng thức nào sau đây sai?
Đẳng thức nào sau đây sai?
Đẳng thức sai là
Trong mặt phẳng tọa độ ![]() cho hai vectơ
cho hai vectơ ![]() và
và ![]() . Tính cosin của góc giữa hai vectơ
. Tính cosin của góc giữa hai vectơ ![]() và
và ![]()
Ta có: .
Cho ba điểm phân biệt ![]() Mệnh đề nào sau đây đúng?
Mệnh đề nào sau đây đúng?
Đáp án chỉ đúng khi ba điểm
thẳng hàng và
nằm giữa
.
Đáp án đúng theo quy tắc ba điểm. Chọn đáp án này.
Cho 4 điểm A, B, C, D phân biệt. Khi đó ![]() bằng
bằng
Ta có:
Cho tam giác ![]() vuông cân tại
vuông cân tại ![]() cạnh
cạnh ![]() Khẳng định nào sau đây sai?
Khẳng định nào sau đây sai?
Dựa vào các đáp án, ta có nhận xét sau:
• đúng, gọi
nằm trên tia đối của tia
sao cho
Và
nằm trên tia đối của tia
sao cho
Dựng hình chữ nhật
suy ra
(quy tắc hình bình hành).
Ta có
• đúng, vì
• sai, xử lý tương tự như ở trên. Chọn đáp án này.
• đúng, vì
Tính độ dài đoạn thẳng ![]() biết tọa độ
biết tọa độ ![]() ?
?
Ta có:
Trong mặt phẳng tọa độ ![]() , cho hai điểm
, cho hai điểm ![]() . Xác định điểm
. Xác định điểm ![]() trên trục hoành sao cho ba điểm
trên trục hoành sao cho ba điểm ![]() thẳng hàng.
thẳng hàng.
Gọi khi đó
Ba điểm thẳng hàng khi và chỉ khi
cùng phương với
.
Biết ![]() và
và ![]() . Câu nào sau đây đúng?
. Câu nào sau đây đúng?
Ta có:
=> và
ngược hướng.
Cho bốn điểm phân biệt ![]() và không cùng nằm trên một đường thẳng. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để
và không cùng nằm trên một đường thẳng. Điều kiện nào trong các đáp án A, B, C, D sau đây là điều kiện cần và đủ để ![]() ?
?
Ta có:
là hình bình hành.
Mặt khác, là hình bình hành
.
Do đó, điều kiện cần và đủ để là
là hình bình hành.
Đẳng thức nào sau đây mô tả đúng hình vẽ bên:
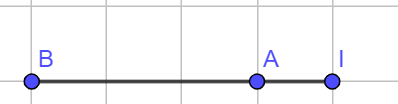
Nhận xét: .
Trên đường thẳng ![]() lấy điểm
lấy điểm ![]() sao cho
sao cho ![]() . Điểm
. Điểm ![]() được xác định đúng trong hình vẽ nào sau đây:
được xác định đúng trong hình vẽ nào sau đây:

Ta có nên
và
và
ngược hướng.
Cho tam giác đều ![]() có cạnh bằng
có cạnh bằng ![]() và chiều cao
và chiều cao ![]() . Mệnh đề nào sau đây là sai?
. Mệnh đề nào sau đây là sai?
+) nên đáp án
đúng.
+) Đáp án
đúng.
+) Đáp án
đúng.
+) Đáp án
sai.
Gọi ![]() là giao điểm của hai đường chéo của hình bình hành
là giao điểm của hai đường chéo của hình bình hành ![]() . Đẳng thức nào sau đây sai?
. Đẳng thức nào sau đây sai?
Đẳng thức sai là
Gọi ![]() là trọng tâm tam giác vuông
là trọng tâm tam giác vuông ![]() với cạnh huyền
với cạnh huyền ![]() Tính độ dài của vectơ
Tính độ dài của vectơ ![]() .
.
Gọi là trung điểm của
Ta có
Cho tam giác ![]() có
có ![]() là trung điểm của
là trung điểm của ![]() . Điểm
. Điểm ![]() xác định
xác định ![]() . Đường thẳng
. Đường thẳng ![]() đi qua
đi qua ![]() song song với
song song với ![]() cắt
cắt ![]() lần lượt tại
lần lượt tại ![]() . Điểm
. Điểm ![]() nằm trên cạnh
nằm trên cạnh ![]() sao cho diện tích các tam giác
sao cho diện tích các tam giác ![]() và
và ![]() bằng nhau. Biết
bằng nhau. Biết ![]() . Tính giá trị của
. Tính giá trị của ![]() ?
?
Hình vẽ minh họa:
Theo định lí Ta – lét ta có:
Mặt khác mà ba điểm
thẳng hàng nên theo định lí Menelaus ta được:
Ta có:
Chú ý rằng khoảng cách từ F đến AB bằng khoảng cách từ A đến DE nên hai tam giác ADE và BGF có cùng diện tích suy ra BG = DE do đó
Ta có:
Mà
Hay
Vậy
Trong mặt phẳng tọa độ ![]() , cho hai vecto
, cho hai vecto ![]() và
và ![]() với
với ![]() . Tìm giá trị của tham số m để
. Tìm giá trị của tham số m để ![]() ?
?
Ta có:
Vậy m = 2 thì hai vecto đã cho vuông góc với nhau.
Cho tam giác ![]() với
với ![]() lần lượt là trung điểm của. Khẳng định nào sau đây sai?
lần lượt là trung điểm của. Khẳng định nào sau đây sai?
Xét các đáp án:
Đáp án . Ta có
Đáp án . Ta có
Đáp án . Ta có
Đáp án . Ta có
Chọn đáp án này.
Cho hình bình hành ABCD tâm O. Mệnh đề nào sau đây là sai?
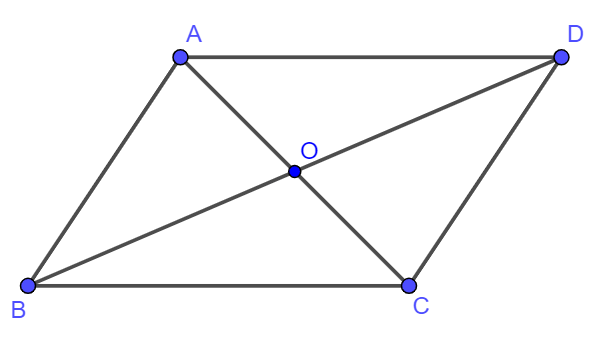
Ta có: (Sai).
Cho hình thoi ![]() cạnh
cạnh ![]() và
và ![]() . Đẳng thức nào sau đây đúng?
. Đẳng thức nào sau đây đúng?
Vì tam giác cân và
, suy ra tam giác
đều cạnh
nên
Cho tam giác ABC đều cạnh ![]() . Đường thẳng
. Đường thẳng ![]() qua
qua ![]() và song song với
và song song với ![]() , lấy điểm
, lấy điểm ![]() . Tính giá trị nhỏ nhất của
. Tính giá trị nhỏ nhất của ![]() khi
khi ![]() di động trên
di động trên ![]() .
.
Hình vẽ minh họa
Kẻ hình bình hành ACBD. Gọi I là trung điểm BD, khi đó, ta có
Ta có:
Dấu “=” xảy ra khi và chỉ khi M trùng với điểm H là hình chiếu vuông góc của điểm I trên đường thẳng .
Cho hình bình hành ABCD. Đẳng thức nào sau đây đúng?
Áp dụng quy tắc hình bình hành tại điểm B ta có:
Cho tam giác ![]() vuông tại
vuông tại ![]()
![]() là trung điểm của
là trung điểm của ![]() Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
Vì là trung điểm của
nên
Cho ![]() Tìm tọa độ của
Tìm tọa độ của ![]()
Ta có
Cho tam giác đều ![]() có cạnh bằng
có cạnh bằng ![]() Tính tích vô hướng
Tính tích vô hướng ![]()
.
Cho ngũ giác ![]() . Từ các đỉnh của ngũ giác đã cho có thể lập được bao nhiêu vectơ có điểm cuối là điểm
. Từ các đỉnh của ngũ giác đã cho có thể lập được bao nhiêu vectơ có điểm cuối là điểm ![]() ?
?
Các vectơ có điểm cuối là điểm là
;
;
;
.
Trong hệ tọa độ ![]() cho ba điểm
cho ba điểm ![]() và
và ![]() Tìm điểm
Tìm điểm ![]() thuộc trục hoành sao cho biểu thức
thuộc trục hoành sao cho biểu thức ![]() đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Ta có
Chọn điểm sao cho
Gọi , từ
ta có
Khi đó
Để nhỏ nhất
nhỏ nhất. Mà
thuộc trục hoành nên
nhỏ nhất khi
là hình chiếu vuông góc của
lên trục hoành
Cho ba điểm ![]() phân biệt. Khi đó:
phân biệt. Khi đó:
Chọn: Điều kiện cần và đủ để thẳng hàng là
cùng phương với
Cho ba điểm phân biệt A, B, C. Khẳng định nào sau đây đúng?
Ta có:
=> Khẳng định sai
=> Khẳng định sai
=> Khẳng định đúng
=> Khẳng định sa
Cho mặt phẳng Oxy, cho ∆ABC có G là trọng tâm. Biết B(4; 1), C(1; –2) và G(2; 1). Tọa độ điểm A là:
Theo bài ra:
G là trọng tâm tam giác ABC nên ta có:
Trong mặt phẳng tọa độ ![]() cho hai điểm
cho hai điểm ![]() và
và ![]() Tìm
Tìm ![]() thuộc trục tung sao cho
thuộc trục tung sao cho ![]() nhỏ nhất.
nhỏ nhất.
Vì .
Ta có:
Ta có:
Suy ra nhỏ nhất khi và chỉ khi
.
Cho ![]() và tọa độ hai điểm
và tọa độ hai điểm ![]() . Biết
. Biết ![]() , tọa độ vecto
, tọa độ vecto ![]() là:
là:
Tọa độ vecto .
Cho tứ giác ![]() . Có bao nhiêu vectơ khác vectơ - không có điểm đầu và cuối là các đỉnh của tứ giác?
. Có bao nhiêu vectơ khác vectơ - không có điểm đầu và cuối là các đỉnh của tứ giác?
Xét các vectơ có điểm là điểm đầu thì có các vectơ thỏa mãn bài toán là
có 3 vectơ.
Tương tự cho các điểm còn lại
Vậy chọn đáp án 12.
Cho ![]() và
và ![]() là các vectơ khác
là các vectơ khác ![]() với
với ![]() là vectơ đối của
là vectơ đối của ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Ta có . Do đó,
và
cùng phương, cùng độ dài và ngược hướng nhau.
Chọn đáp án sai là: Hai vectơ chung điểm đầu.
Cho ba điểm O, A, B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng ![]() là:
là:
Chọn đáp án: Tam giác OAB cân tại O.
Gọi là trung điểm
.
Ta có: (do
).
Cho tam giác ![]() và điểm
và điểm ![]() thỏa mãn
thỏa mãn ![]() Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
Gọi lần lượt là trung điểm
và trọng tâm tam giác
Vì
là trung điểm
nên
Theo bài ra, ta có suy ra
thẳng hàng
Mặt khác là trọng tâm của tam giác
Do đó, ba điểm
thẳng hàng.
