Lớp 11 Toán 11 - Cánh Diều

Đề kiểm tra 45 phút Toán 11 Chương 8 Cánh Diều

Cùng nhau thử sức với bài kiểm tra 45 phút Toán 11 Cánh Diều Chương 8: Quan hệ vuông góc trong không gian. Phép chiếu vuông góc nha!

  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của điểm S lên mặt phẳng (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Gọi α là số đo của góc giữa đường thẳng SA và mặt phẳng (ABC). Tính tan α.

    Hình chiếu của SA lên mặt phẳng (ABC) là AH

    => Góc giữa SA và mặt phẳng (ABC) là \widehat{SAH}

    Tam giác ABC và SBC là các tam giác đều cùng cạnh a

    AH = SH =\frac{a\sqrt{3}}{2}

    Vậy tan α = 1

  • Câu 2: Vận dụng cao

    Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các cạnh AB = 2, AD = 3, AA’ = 4. Góc giữa hai mặt phẳng (AB’D’) và (A’C’D) là α. Tính giá trị gần đúng của α.

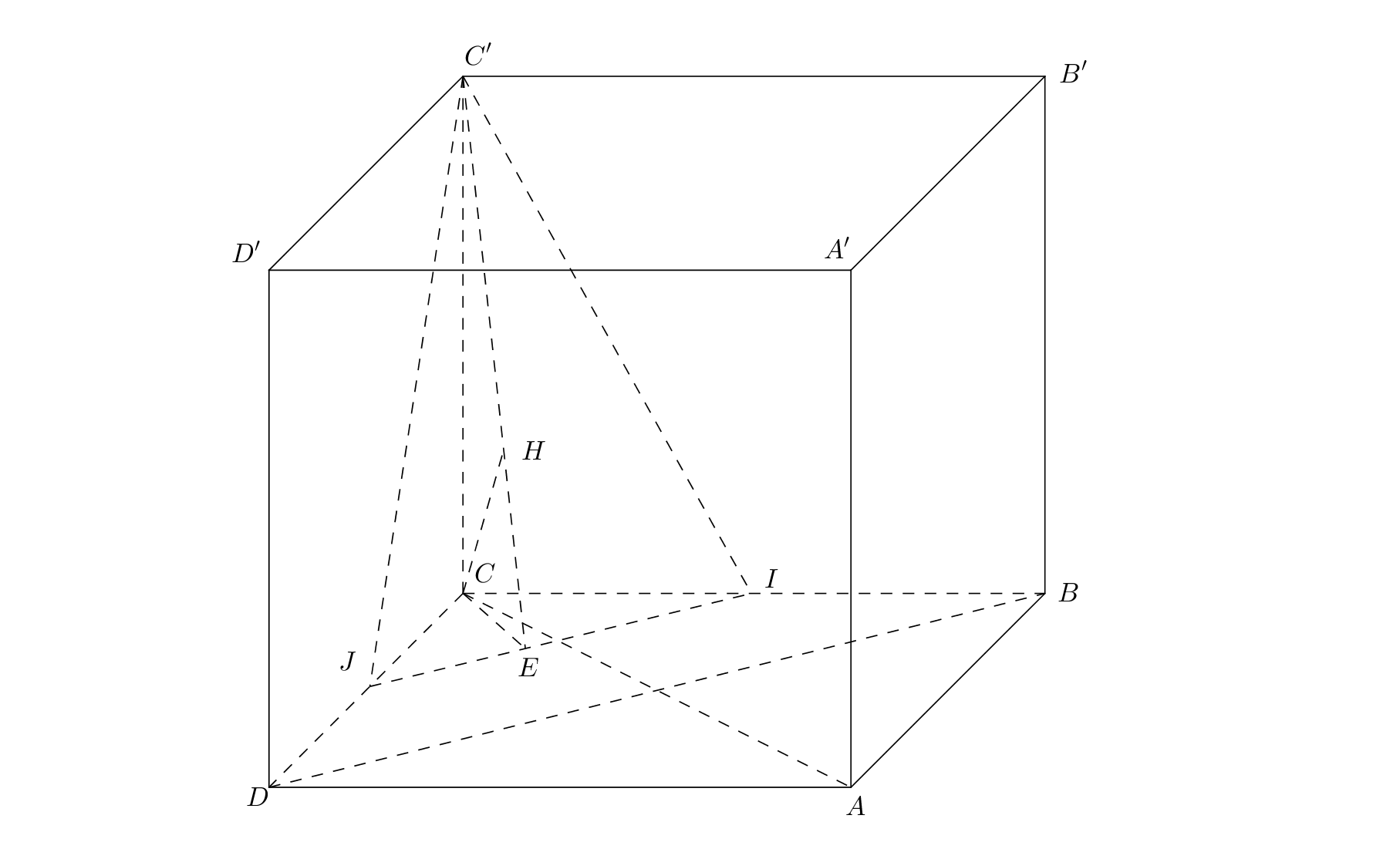
    Hình vẽ minh họa:

    Phần 1: Xác định góc

    Bước 1: Tìm giao tuyến giữa hai mặt phẳng:

    Trong mặt phẳng (ADD’A’) gọi E là giao điểm của AD’ và A’D.

    Trong mặt phẳng (A’B’C’D’) gọi F là giao điểm của B’D’ và A’C’.

    Khi đó EF là giao tuyến của hai mặt phẳng (AB’D’) và (A’C’D).

    Bước 2: Trong mỗi mặt phẳng, ta cần tìm đường thẳng vuông góc với giao tuyến:

    Trong mặt phẳng (DA’C’) kẻ A’H ⊥ EF tại H, A’H cắt DC’ tại K.

    Ta chứng minh D’H ⊥ EF.

    Ta có: \left\{ \begin{matrix} DC’\bot A’K \\ DC’\bot A’D’ \\ \end{matrix} ight.\ \Rightarrow DC’\bot(A’D’K) \Rightarrow DC’\bot D’H

    Mặt khác: \left\{ \begin{matrix} DC’\bot D’H \\ D’C//EF \\ \end{matrix} ight.\ \Rightarrow DH’\bot EF

    Bước 3: Xác định góc giữa hai mặt phẳng:

    Ta có: \left\{ \begin{matrix} D’H \subset (AB’D’) \\ D’H\bot EF \\ A’H \subset (DA’C’) \\ A’H\bot EF \\ (AB’D’) \cap (DA’C’) = EF \\ \end{matrix} ight.

    => α = ((AB’D’), (DA’C’)) = (D’H, A’H)

    Phần 2: Tính góc α:

    Ta sẽ sử dụng định lý cosin trong tam giác A’HD’

    Bước 1: Chứng minh tam giác A’HD’ cân:

    Trong tam giác A’DC’ ta có EF là đường trung bình, nên suy ra H là trung điểm A’K.

    Vì A’D’ ⊥ (DD’C’C) nên A’D’ ⊥ D’K.

    Do đó tam giác A’D’K vuông tại D’.

    Xét tam giác A’D’K vuông tại D’ có D’K là đường trung tuyến ứng với cạnh huyền nên D’H = A’H = A’K/2

    Bước 2: Tính độ dài cạnh A’K:

    Ta tính đường cao A’K của tam giác ADC’ thông qua diện tích.

    Áp dụng định lý Pi – ta - go ta tính được độ dài các cạnh tam giác A’DC’ là: A'D = 5;A'C' = \sqrt{13};D'C = 2\sqrt{5}

    Sử dụng công thức Hê-rông ta tính được S_{A'DC'} = \sqrt{61}

    Mặt khác

    S_{A'DC'} = \frac{1}{2}A'K.DC' = \frac{1}{2}A'K.2\sqrt{5}

    \Rightarrow A'K = \frac{\sqrt{305}}{5}

    Từ đó suy ra D’H = A’H = A’K/2 = \frac{\sqrt{305}}{10}

    Bước 3: Tính góc α bằng định lý cosin:

    Trong tam giác A’HD’ ta có:

    \cos\widehat{A'HD'} = \frac{HA^{2} + HD^{2} - A'D'^{2}}{2HA.HD}

    = \dfrac{2\left( \dfrac{\sqrt{305}}{10}ight)^{2} - 3^{2}}{2\left( \dfrac{\sqrt{305}}{10} ight)^{2}} = -\dfrac{29}{61}

    \Rightarrow \widehat{A'HD'} = 118,4^{0}

    Do đó góc giữa hai đường thẳng A’H và D’H bằng 61,60

    Vậy α = 61,60

  • Câu 3: Thông hiểu

    Cho hình chóp S.ABC có SA\bot(ABC), đáy ABC là tam giác cân tại A. Gọi M là trung điểm của BC, J là trung điểm của BM. Xác định góc giữa hai mặt phẳng (SBC) và (ABC)?

    Hình vẽ minh họa

    Dễ thấy (SBC) \cap (ABC) = BC

    Ta có tam giác ABC cân tại A, M là trung điểm của BC suy ra AM\bot BC

    Theo giả thiết SA\bot(ABC). Khi đó \left\{ \begin{matrix} BC\bot AM \\ BC\bot SA \\ \end{matrix} ight.\ \Rightarrow BC\bot(SAM) \Rightarrow BC\bot SM

    Ta được \left\{ \begin{matrix} (SBC) \cap (ABC) = BC \\ AM\bot BC \\ SM\bot BC \\ \end{matrix} ight.

    \Rightarrow \left( \widehat{(SBC);(ABC)} ight) = \widehat{SMA}

  • Câu 4: Thông hiểu

    Cho khối hộp chữ nhật ABCD.A'B'C'D' có đáy là hình vuông, đường chéo BD = 4a. Biết góc giữa hai mặt phẳng (A'BD) và mặt phẳng (ABCD) bằng 60^{0}. Khi đó thể tích hình hộp chữ nhật bằng bao nhiêu?

    Hình vẽ minh họa

    Gọi góc giữa mặt phẳng (A'BD) và mặt phẳng (ABCD)là \alphavà O = AC \cap BD

    Ta có: \left\{ \begin{matrix} AO\bot BD \\ AA'\bot BD \\ \end{matrix} ight.\ \Rightarrow A'O\bot BD

    \Rightarrow \alpha = (AO;A'O) = \widehat{AOA'} = 60^{0}

    Ta có ABCD là hình vuông, BD = 4a nên AB = AD = 2a\sqrt{2}

    Ta có: AO = \frac{1}{2}AC = \frac{1}{2}BD = 2a

    Xét tam giác AOA’ có AA' = AO.tan60^{0} = 2a\sqrt{3}

    \Rightarrow V_{ABCD.A'B'C'D'} = AA'.S_{ABCD} = 2a\sqrt{3}.8a^{2} = 16a^{3}\sqrt{3}

  • Câu 5: Nhận biết

    Chọn khẳng định đúng trong các khẳng định sau?

    Ta có:

    “Trong không gian hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau” sai do hai đường thẳng phân biệt cùng vuông góc với một đường thẳng có thể cắt nhau hoặc chéo nhau.

    “Trong không gian hai mặt phẳng cùng vuông góc với một đường thẳng thì song song với nhau” sai do hai mặt phẳng cùng vuông góc với một đường thẳng có thể trùng nhau.

    “Trong không gian hai đường thẳng không có điểm chung thì song song với nhau” sai do trong không gian hai đường thẳng không có điểm chung có thể chéo nhau.

    Vậy khẳng định đúng là: “Trong không gian hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.”

  • Câu 6: Nhận biết

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với mặt phẳng (ABCD). Tìm khẳng định đúng trong các khẳng định sau:

    Khẳng định đúng là “AB vuông góc với mặt phẳng (SAD)”

    Thật vậy, do SA ⊥ (ABCD) nên SA ⊥ AB

    Mặt khác AB ⊥ AD.

    Từ đó suy ra AB ⊥ (SDA)

  • Câu 7: Nhận biết

    Hình tứ diện ABCD có AB = AC = AD = 3 và AB, AC, AD đôi một vuông góc với nhau. Diện tích của tam giác BCD bằng:

    Do ∆BCD là tam giác đều cạnh \sqrt{18} nên có diện tích là S_{BCD} = \frac{18\sqrt{3}}{4} = \frac{9\sqrt{3}}{2}

  • Câu 8: Thông hiểu

    Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Gọi D là trung điểm cạnh BC. Biết AA' = 2a, khoảng cách giữa hai đường thẳng A'B và C'D là:

    Hình vẽ minh họa

    Gọi D' là trung điểm của B'C', ta có BDC'D' là hình bình hành

    \Rightarrow C'D//BD' \Rightarrow C'D//(A'BD').

    Kẻ B'H \bot BD'.

    Ta có: \left. \ \begin{matrix}A'D'\bot B'C' \\A'D'\bot BB' \\\end{matrix} ight\} \Rightarrow A'D'\bot(BCC'B')\Rightarrow A'D'\bot B'H.

    \left. \ \begin{matrix} B'H\bot BD' \\ B'H\bot A'D' \\ \end{matrix} ight\} \Rightarrow B'H\bot(A'BD')

    Suy ra,

    d(A'B,C'D) = d\left( C'D;(A'BD') ight) = d\left( C';(A'BD') ight) = d\left( B';(A'BD') ight) = B'H

    Ta có: B'D' = \frac{a}{2}; BB'= 2a.

    Xét \Delta BB'D' vuông tại B' ta có:

    \frac{1}{B'H^{2}} = \frac{1}{BB'^{2}} + \frac{1}{B'D'^{2}} = \frac{1}{4a^{2}} + \frac{4}{a^{2}} \Rightarrow BH = \frac{2a}{\sqrt{17}}

  • Câu 9: Vận dụng

    Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a. Gọi α là góc giữa hai mặt phẳng (SBD) và (SCD). Mệnh đề nào sau đây đúng?

    Hình vẽ minh họa:

    Gọi O = AC ∩BD. Do hình chóp S.ABCD đều => SO ⊥ (ABCD).

    Gọi M là trung điểm của SD.

    Tam giác SCD đều nên CM ⊥ SD.

    Tam giác SBD có SB = SD = a, BD = a\sqrt{2} nên vuông tại S

    => SB ⊥ SD => OM ⊥ SD

    => ((SBD),(SCD)) = (OM, CM) = \widehat{OMC}

    Ta có: \left\{ \begin{matrix} OC\bot BD \\ OC\bot SO \\ \end{matrix} ight.\ \Rightarrow OC\bot(SBD) \Rightarrow OC\bot OM

    Tam giác vuông MOC ta có:

    \tan\widehat{OMC} = \frac{OC}{OM} = \sqrt{2}

  • Câu 10: Vận dụng

    Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = 2a, BC = a. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AB, góc giữa đường thẳng SC và mặt phẳng đáy bằng 600. Tính cosin góc giữa hai đường thẳng SB và AC.

    Tính cosin góc giữa hai đường thẳng SB và AC

    +) Ta có:

    \begin{matrix} \overrightarrow {SB} .\overrightarrow {AC} = \left( {\overrightarrow {SH} + \overrightarrow {HB} } ight)\left( {\overrightarrow {AB} + \overrightarrow {BC} } ight) \hfill \\ = \overrightarrow {SH} .\overrightarrow {AB} + \overrightarrow {SH} .\overrightarrow {BC} + \overrightarrow {HB} .\overrightarrow {AB} + \overrightarrow {HB} .\overrightarrow {BC} \hfill \\ = \overrightarrow {HB} .\overrightarrow {AB} + \overrightarrow {HB} .\overrightarrow {BC} \hfill \\ = \dfrac{1}{2}A{B^2} = 2{a^2} \hfill \\ \end{matrix}

    +) Mặt khác

    \begin{matrix} AC = a\sqrt 5 ;CH = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \hfill \\ SH = CH.\tan \widehat {SCH} = a\sqrt 6 \hfill \\ SB = \sqrt {S{H^2} + H{B^2}} = \sqrt {{{\left( {a\sqrt 6 } ight)}^2} + {a^2}} = a\sqrt 7 \hfill \\ \end{matrix}

    => \cos \left( {SB,AC} ight) = \frac{{\left| {\overrightarrow {SB} .\overrightarrow {AC} } ight|}}{{SB.AC}} = \frac{{2{a^2}}}{{a\sqrt 7 .a\sqrt 5 }} = \frac{2}{{\sqrt {35} }}

  • Câu 11: Thông hiểu

    Cho tứ diện đều ABCD. I là trung điểm của AB. Góc giữa hai đường thẳng IC và AD có cosin bằng:

    Hình vẽ minh họa:

    Góc giữa hai đường thẳng IC và AD

    Giả sử cạnh tứ diện đều bằng a. Khi đó:

    \begin{matrix} \overrightarrow {AD} .\overrightarrow {AB} = {a^2}.\cos {60^0} = \dfrac{{{a^2}}}{2} \hfill \\ \overrightarrow {AC} .\overrightarrow {AD} = \dfrac{{{a^2}}}{2} \hfill \\ \end{matrix}

    Ta có:

    \begin{matrix} \overrightarrow {IC} = \overrightarrow {AC} - \overrightarrow {AI} = \overrightarrow {AC} - \dfrac{1}{2}\overrightarrow {AB} \hfill \\ \Rightarrow \overrightarrow {IC} .\overrightarrow {AD} = \dfrac{{{a^2}}}{2} - \dfrac{{{a^2}}}{4} = \dfrac{{{a^2}}}{4} \hfill \\ \end{matrix}

    \begin{matrix} \cos \left( {\widehat {IC;AD}} ight) = \dfrac{{\left| {\overrightarrow {IC} .\overrightarrow {AD} } ight|}}{{IC.AD}} \hfill \\ \Rightarrow \cos \left( {\widehat {IC;AD}} ight) = \dfrac{{{a^2}}}{4}:\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{1}{{2\sqrt 3 }} \hfill \\ \end{matrix}

  • Câu 12: Thông hiểu

    Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a. Biết \left( (SAB);(ABCD) ight) = 90^{0} và tam giác SAB đều. Xác định thể tích hình chóp S.ABCD?

    Hình vẽ minh họa

    Gọi H là trung điểm của AB

    Tam giác SAB đều nên SH\bot AB

    Ta có: \left\{ \begin{matrix} SH\bot AB \\ (SAB)\bot(ABCD) \\ SH \subset (SAB) \\ AB = (SAB) \cap (ABCD) \\ \end{matrix} ight.\ \Rightarrow SH\bot(ABCD)

    Vậy SH là đường cao của hình chóp

    Xét tam giác AHS vuông tại H ta có:

    SH = \sqrt{SA^{2} - AH^{2}} = \sqrt{a^{2} - \left( \frac{a}{2} ight)^{2}} = \frac{a\sqrt{3}}{2}

    Thể tích khối chóp là: V = \frac{1}{3}B.h = \frac{1}{3}.a^{2}.\frac{a\sqrt{3}}{2} = \frac{a^{3}\sqrt{3}}{6}

  • Câu 13: Vận dụng cao

    Cho hình chóp đều S.ABC có đáy là tam giác ABC là tam giác đều tâm O cạnh bằng a, OS = 2a. Gọi M là điểm thuộc đoạn OA (M khác A và O). Mặt phẳng đi qua M và vuông góc với AO là mặt phẳng (α). Đặt AM = x. Tính diện tích thiết diện S của thiết diện tạo bởi (α) với hình chóp S.ABC.

    Hình vẽ minh họa:

    Ta có: S.ABC là hình chóp đều nên SO ⊥ (ABC)

    => SO ⊥ AA’ mà (α) ⊥ AA’ => SO // (α)

    Chứng minh tương tự ta có: BC // (α)

    Qua M kẻ IJ // BC với I ∈ AB, J ∈ AC, kẻ MK // SO với K ∈ SA.

    Khi đó thiết diện là tam giác KIJ

    Diện tích ram giác IJK là S_{IJK} = \frac{1}{2}IJ.MK

    Trong tam giác ABC có:

    \frac{IJ}{BC} = \frac{AM}{AA'} \Rightarrow IJ = \frac{AM.BC}{AA'} = \frac{2x\sqrt{3}}{3}

    Tương tự trong tam giác SAO, ta có:

    \frac{MK}{SO} = \frac{AM}{AO} \Rightarrow MK = \frac{AM.SO}{AO} = 2x\sqrt{3}

    Vậy S_{IJK} = \frac{1}{2}.\frac{2x\sqrt{3}}{3}.2x\sqrt{3} = 2x^{2}

  • Câu 14: Nhận biết

    Cho hình chóp S.ABC có đường thẳng SA vuông góc với đáy (ABC), SA = 2a. Khoảng cách từ điểm S đến đường thẳng AB bằng:

    Vì SA vuông góc với đáy (ABC) nên SA\bot AB \Rightarrow d(S,AB) = SA = 2a

  • Câu 15: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a. Giả sử góc BAD bằng 600. Khoảng cách từ điểm S đến mặt phẳng (ABCD) bằng:

    Hình vẽ minh họa

    Khoảng cách từ điểm S đến mặt phẳng (ABCD)

    Từ S vẽ SO ⊥ (ABCD) ⇒ OA = OB = OC (là hình chiếu của các đường xiên bằng nhau) ⇒ O là tâm đường tròn ngoại tiếp đáy

    \begin{matrix} S{O^2} = S{A^2} - A{O^2} \hfill \\ = {a^2} - {\left( {\dfrac{{a\sqrt 3 }}{2}} ight)^2} = \dfrac{{{a^2}}}{4} \hfill \\ \Rightarrow SO = \dfrac{a}{2} \hfill \\ \end{matrix}

  • Câu 16: Thông hiểu

    Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Góc tạo bởi cạnh bên SA và mặt phẳng đáy bằng 60^{0}. Thể tích khối chóp S.BCD bằng bao nhiêu?

    Hình vẽ minh họa

    Gọi O là giao điểm của hai đường chéo AC và BD

    Ta có: tam giác SAC cân, O là trung điểm của AC nên SO\bot CA

    Tương tự tam giác SBD cân, O là trung điểm của BD nên SO\bot BD

    \Rightarrow SO\bot(ABCD)

    Suy ra OA là hình chiếu vuông góc của SA lên mặt phẳng đáy

    \Rightarrow \left( SA;(ABCD) ight) = \widehat{SAO} = 60^{0}

    ABCD là hình vuông nên OA = \frac{1}{2}AC = \frac{a\sqrt{2}}{2}

    Xét tam giác vuông SOA ta có:

    SO = AO.\tan\widehat{SDO} =\frac{a\sqrt{2}}{2}.\tan60^{0} = \frac{a\sqrt{6}}{3}

    \Rightarrow S_{BCD} = \frac{a^{2}}{2}

    \Rightarrow V_{S.BCD} = \frac{1}{3}.SO.S_{BCD} = \frac{1}{3}.\frac{a\sqrt{6}}{2}.\frac{a^{2}}{2} = \frac{a^{3}\sqrt{6}}{12}

  • Câu 17: Thông hiểu

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, các cạnh AB = AC = a, các góc \widehat{SBA} = \widehat{SCA} = 90^{0}. Gọi H là hình chiếu vuông góc của S trên (ABC) và SH = a\sqrt{2}. Tính cosin góc giữa hai mặt phẳng (SAB) và (SAC).

    Đáp án: 1/3 (Ghi đáp án dưới dạng phân số tối giản a/b).

    Đáp án là:

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, các cạnh AB = AC = a, các góc \widehat{SBA} = \widehat{SCA} = 90^{0}. Gọi H là hình chiếu vuông góc của S trên (ABC) và SH = a\sqrt{2}. Tính cosin góc giữa hai mặt phẳng (SAB) và (SAC).

    Đáp án: 1/3 (Ghi đáp án dưới dạng phân số tối giản a/b).

    Hình vẽ minh họa

    Gọi (\alpha) là mặt phẳng qua B và vuông góc với AB \Rightarrow (\alpha) \cap (ABC) = Bt//AC.

    Gọi (\beta) là mặt phẳng qua C và vuông góc với AC

    \Rightarrow (\beta) \cap (ABC) =Ct'//AB

    Khi đó, (\alpha) \cap (\beta) = SH với H = Bt \cap Ct' là đỉnh thứ tư của hình vuông ABHC.

    Khi đó: \Delta SAB,\ \ \Delta SAC là hai tam giác vuông bằng nhau có SB = SC = a\sqrt{3},SA = 2a.

    Gọi I là chân đường cao hạ từ đỉnh B của tam giác SAB, ta có BI\bot SA,CI\bot SA.

    Vậy góc giữa hai mặt phẳng (SAB) và (SAC) là (IB;IC).

    Xét \Delta IBC cân tại I có IB = IC = \frac{a\sqrt{3}.a}{2a} = \frac{a\sqrt{3}}{2},BC = a\sqrt{2}.

    Ta có: \cos\widehat{BIC} = \frac{IB^{2} +IC^{2} - BC^{2}}{2IB.IC}= \dfrac{\dfrac{3a^{2}}{4} + \dfrac{3a^{2}}{4} -2a^{2}}{2.\dfrac{3a^{2}}{4}} = - \dfrac{1}{3}.

    Vậy cosin góc giữa hai mặt phẳng (SAB) và (SAC) bằng \frac{1}{3}.

  • Câu 18: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA\bot(ABCD); SA = AB. Gọi trung điểm các cạnh BC;SC lần lượt là E;F. Tính \left( EF;(SAD) ight)?

    Hình vẽ minh họa

    Ta có: \left\{ \begin{matrix} AB\bot AD \\ AB\bot SA \\ \end{matrix} ight.\ \Rightarrow AB\bot(SAD)

    \Rightarrow \left( EF;(SAD) ight) = \left( BS;(SAD) ight) = (BS;AS) = \widehat{BSA}

    Xét tam giác SAB vuông tại A có SA = AB

    \Rightarrow \widehat{BSA} = 45^{0}

    \Rightarrow \left( EF;(SAD) ight) = \widehat{BSA} = 45^{0}

  • Câu 19: Thông hiểu

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ⊥ (ABC), H là chân đường cao kẻ từ A của tam giác SAB. Khẳng định nào dưới đây là khẳng định sai?

    Hình vẽ minh họa:

    Ta có: SA ⊥ (ABC) mà BC thuộc (ABC)

    => SA ⊥ BC

    Xét tam giác ABC vuông tại B ta có:

    AB ⊥ BC

    => BC ⊥ (SAB) => BC ⊥ AH

    Khi đó: AH ⊥ SB, AH ⊥ BC => AH ⊥ (SBC) => AH ⊥ SC

    Nếu có: AH ⊥ AC trong khi SA ⊥ AC thì AC ⊥ (SAB)

    => AC ⊥ AB (vô lí)

  • Câu 20: Thông hiểu

    Cho hình tứ diện OABC có OA, OB, OC đôi một vuông góc. Gọi I là hình chiếu của điểm O trên mặt phẳng (ABC). Tam giác ABC là:

    Giả sử tam giác ABC vuông tại A

    Khi đó B có hai đường thẳng BO và BA cùng vuông góc với mặt phẳng (OCA) 

    Điều này vô lí, do đó tam giác ABC không thể là tam giác vuông

    Từ O hạ OH \perp AB => CH \perp AB (theo định lí ba đường vuông góc)

    Vì điểm H giữa hai điểm A và B nên tam giác ABC không thể có góc tù.

    Suy ra ABC có ba góc nhọn.

  • Câu 21: Nhận biết

    Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA\bot(ABCD);SA = a\sqrt{2}. Tính \left( SC;(ABCD) ight)?

    Hình vẽ minh họa

    Ta có: SA\bot(ABCD) nên góc giữa SC và mặt phẳng đáy bằng góc \widehat{SCA}.

    Ta có: SA = a\sqrt{2};AC = a\sqrt{2}

    \Rightarrow \tan\widehat{SCA} = \frac{SA}{AC} = 1 \Rightarrow \widehat{SCA} = 45^{0}

    Vậy \left( SC;(ABCD) ight) = 45^{0}

  • Câu 22: Vận dụng cao

    Cho hình chóp S.ABCD có đáy là hình bình hành và SA = SB = SC = 11, \widehat{SAB} = 30^{0}, \widehat{SBC} = 60^{0};\widehat{SCA} =45^{0}. Tính khoảng cách d giữa hai đường thẳng AB và SD?

    Hình vẽ minh họa:

    Dựa vào định lý cosin ta dễ dàng tính được BC = 11, AB = 11\sqrt{3};AC = 11\sqrt{2}

    => ∆ABC vuông tại C

    Do SA = SB = SC, nên hình chiếu của S xuống mặt phẳng (ABC) trùng với trung điểm H của AB

    => SH ⊥ (ABCD) và SH =SA.sin\widehat{SAB} = \frac{11}{2}

    Kẻ HK ⊥ CD, AP ⊥ CD, tứ giác APKH là hình chữ nhật, HK = AP = \frac{11\sqrt{6}}{3}(Do \frac{1}{AP^{2}} = \frac{1}{AD^{2}} +\frac{1}{AC^{2}})

    Trong tam giác vuông SHK, kẻ HI ⊥ SK

    Do AB // CD => d(AB, SD) = d(H, SD) = HI

    Ta có: \frac{1}{HI^{2}} =\frac{1}{SH^{2}} + \frac{1}{SK^{2}} \Rightarrow HI =\sqrt{22}

  • Câu 23: Nhận biết

    Cho khối chóp S.ABC có SA\bot(ABC) biết độ dài các cạnh SA = 4cm,AB = 6cm, BC = 10cm;CA = 8cm. Thể tích khối chóp S.ABC là:

    Hình vẽ minh họa

    Ta có:

    AB^{2} + AC^{2} = 6^{2} + 8^{2} = 10^{2} = BC^{2}

    Nên tam giác ABC vuông tại A

    Suy ra S_{ABC} = \frac{1}{2}AB.AC = 24

    Vậy V_{S.ABC} = \frac{1}{3}.S_{ABC}.SA = 32cm^{3}

  • Câu 24: Nhận biết

    Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và A’C’ bằng:

    Do BD và A’C’ lần lượt nằm trên hai mặt phẳng (ABCD) và (A’B’C’D’) song song với nhau nên d(A’C’, BD) = d((ABCD),(A’B’C’D’)).

    Mà ABCD.A’B’C’D’ là hình lập phương nên ta có d((ABCD), (A’B’C’D’)) = AA’ = a. Vậy d(A’C’, BD) = a.

  • Câu 25: Nhận biết

    Cho đường thẳng a và mặt phẳng (P). Có bao nhiêu mặt phẳng đi qua a và vuông góc với mặt phẳng (P)?

    Có một khi a không vuông góc với (P), có vô số khi a vuông góc với (P).

  • Câu 26: Vận dụng cao

    Cho hình hộp chữ nhật ABCD.A’B’C’D’ nội tiếp mặt cầu (S) có bán kính R = \frac{{\sqrt {17} }}{2}. Gọi I; J là trung điểm BC, CD và \alpha là góc giữa đường thẳng AC’ và mặt phẳng (C’IJ). Giá trị lớn nhất của \sin \alpha là

    Giá trị lớn nhất của góc giữa đường thẳng và mặt phẳng

    Đặt CD = a\,,\,CB = b\,,CC' = c\,\,\,\left( {a,b,c > 0} ight).

    AC{'^2} = {a^2} + {b^2} + {c^2} = 17.

    Gọi K là hình chiếu của A lên (C’IJ)

    \left( {\widehat {AC',\left( {C;{\text{IJ}}} ight)}} ight) = \left( {\widehat {AC',AK}} ight) = \alpha

    Ta có \sin \alpha = \frac{{d\left( {A,\left( {C'{\text{IJ}}} ight)} ight)}}{{AC'}} = \frac{{3d\left( {C,\left( {C'{\text{IJ}}} ight)} ight)}}{{\sqrt {17} }}

    Trong (ABCD) kẻ tại E

    \left\{ \begin{gathered} IJ \bot CE \hfill \\ IJ \bot CC\prime \hfill \\ CE \subset \left( {CEC'} ight) \hfill \\ \,CC' \subset \left( {CEC'} ight) \hfill \\ CE \cap CC' = C \hfill \\ \end{gathered} ight. \Rightarrow IJ \bot \left( {CEC'} ight) \Rightarrow \left( {C'IJ} ight) \bot \left( {CEC'} ight)

    Trong (CEC’) kẻ CH \bot C'E tại H

    Suy ra d\left( {C,\left( {C'{\text{IJ}}} ight)} ight) = CH = h

    Do đó \sin \alpha = \frac{{3h}}{{\sqrt {17} }}

    Ta có:

    \begin{matrix} \dfrac{1}{{{h^2}}} = \dfrac{1}{{{c^2}}} + \dfrac{4}{{{a^2}}} + \dfrac{4}{{{b^2}}} = \dfrac{1}{{{c^2}}} + 4\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} ight) \geqslant \dfrac{1}{{{c^2}}} + \dfrac{{16}}{{{a^2} + {b^2}}} \hfill \\ \Leftrightarrow \dfrac{1}{{{h^2}}} \geqslant \frac{1}{{{c^2}}} + \dfrac{{16}}{{17 - {c^2}}} = \dfrac{{17 - {c^2} + {c^2}}}{{17{c^2}}} + \dfrac{{16\left( {17 - {c^2} + {c^2}} ight)}}{{17\left( {17 - {c^2}} ight)}} \hfill \\ \Leftrightarrow \dfrac{1}{{{h^2}}} \geqslant \dfrac{{17 - {c^2}}}{{17{c^2}}} + \dfrac{{16{c^2}}}{{17\left( {17 - {c^2}} ight)}} + 1 \geqslant 2.\dfrac{4}{{17}} + 1 = \dfrac{{25}}{{17}} \Leftrightarrow h \leqslant \dfrac{{\sqrt {17} }}{5}. \hfill \\ \Rightarrow \sin \alpha \leqslant \dfrac{3}{5}. \hfill \\ \end{matrix}

    Vậy đạt giá trị lớn nhất là \frac{3}{5}

    Dấu xảy ra khi: \left\{ \begin{gathered} {a^2} = {b^2} = \frac{{34}}{5} \hfill \\ {c^2} = \frac{{17}}{5} \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} a = b = \sqrt {\frac{{34}}{5}} \hfill \\ c = \sqrt {\frac{{17}}{5}} \hfill \\ \end{gathered} ight.

  • Câu 27: Thông hiểu

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy. Gọi H, K lần lượt là hình chiếu vuông góc của A trên các cạnh SB, SC. Giả sử HK cắt BC tại D. Khi đó:

    a) \widehat{(AC;AD)} = 90^{0} Đúng||Sai

    b) AH\bot(SBC) Đúng||Sai

    c) \widehat{(SC;HK)} = 90^{0} Đúng||Sai

    d) Tam giác SBC cân tại B. Sai||Đúng

    Đáp án là:

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy. Gọi H, K lần lượt là hình chiếu vuông góc của A trên các cạnh SB, SC. Giả sử HK cắt BC tại D. Khi đó:

    a) \widehat{(AC;AD)} = 90^{0} Đúng||Sai

    b) AH\bot(SBC) Đúng||Sai

    c) \widehat{(SC;HK)} = 90^{0} Đúng||Sai

    d) Tam giác SBC cân tại B. Sai||Đúng

    \widehat{(AC;AD)} = 90^{0} đúng

    AH\bot(SBC) đúng

    \widehat{(SC;HK)} = 90^{0} đúng

    Tam giác SBC cân tại B. sai

  • Câu 28: Vận dụng

    Cho tứ diện ABCD có AB, BC, BD đôi một vuông góc. Trong các khẳng định dưới đây khẳng định nào đúng?

    Hình vẽ minh họa:

    Chọn khẳng định đúng

    \widehat {\left( {CD;\left( {ABD} ight)} ight)} = \widehat {CBD} sai vì

    CB ⊥ BD, CB ⊥ BA => CB ⊥ (ABD)

    => B là hình chiếu của C trên mặt phẳng (ABD)

    => \widehat {\left( {CD;\left( {ABD} ight)} ight)} = \widehat {CDB}

    \widehat {\left( {AC;\left( {BCD} ight)} ight)} = \widehat {ACB} đúng vì

    AB ⊥ BC, AB ⊥ BD => AB ⊥ (BCD)

    => B là hình chiếu của A trên mặt phẳng (BCD)

    => \widehat {\left( {AC;\left( {BCD} ight)} ight)} = \widehat {ACB}

    \widehat {\left( {AD;\left( {ABC} ight)} ight)} = \widehat {ADB} sai vì

    BD⊥ BA, BD ⊥ BC => BD ⊥ (ABC)

    => B là hình chiếu của D trên mặt phẳng (ABC)

    => \widehat {\left( {AD;\left( {ABC} ight)} ight)} = \widehat {DAB}

    \widehat {\left( {AC;\left( {ABD} ight)} ight)} = \widehat {CBA} sai vì

    => B là hình chiếu của C trên mặt phẳng (ABD)

    => \widehat {\left( {AC;\left( {ABD} ight)} ight)} = \widehat {CAB}

  • Câu 29: Thông hiểu

    Cho hình chóp tam giác S.ABC có SA = SB = SC = AB = AC = a và BC = a\sqrt{2}. Kết quả nào dưới đây đúng?

    Ta có:

    BC^{2} = AB^{2} + AC^{2} suy ra tam giác ABC vuông tại A

    => M là tâm đường tròn ngoại tiếp tam giác ABC.

    Vì SA = SB = SC nên SM là đường cao của hình chóp S.ABC.

    Hình vẽ minh họa

    Gọi N, I lần lượt là trung điểm cạnh AC và SB.

    Ta có: MN // AB và IM // SC nên (SC,AB) = (IM,MN)

    Mà BN = \sqrt{AB^{2} + AN^{2}} = \sqrt{a^{2} + \frac{a^{2}}{4}} = \frac{a\sqrt{5}}{2}

    SN = \sqrt{SC^{2} - NC^{2}} = \sqrt{a^{2} - \frac{a^{2}}{4}} = \frac{a\sqrt{3}}{2}

    MN = \frac{a}{2};MI = \frac{a}{2}

    Xét tam giác IMN có

    \cos\widehat{NMI} = \dfrac{MN^{2} +IM^{2} - IN^{2}}{2.MN.IM}= \dfrac{\dfrac{a^{2}}{4} + \dfrac{a^{2}}{4} -\dfrac{3a^{2}}{4}}{2.\dfrac{a}{2}.\dfrac{a}{2}} = -\dfrac{1}{2}

    \Rightarrow \widehat{NMI} = 120^{0}

    \Rightarrow (SC,AB) = (IM,MN) = 60^{0}

  • Câu 30: Vận dụng

    Cho tứ diện ABCD có các cạnh AB,AC,AD đôi một vuông góc với nhau; AB = 8a;AC = 5a;AD = 6a. Gọi trung điểm của các cạnh BC,CD,DB lần lượt là J;Q;K. Tính thể tích tứ diện AJQK?

    Hình vẽ minh họa

    Ta có: V_{ABCD} = \frac{1}{2}AB.\frac{1}{2}AD.AC = 60a^{3}

    Nhận thấy S_{JQK} = \frac{1}{2}S_{JQKD} = \frac{1}{4}S_{BCD}

    V_{JQK} = \frac{1}{4}.V_{ABCD} = 15a^{3}

  • Câu 31: Vận dụng

    Cho hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng x và \widehat{BAD} = \widehat{DAA'} = \widehat{A'AB} = 60^{0}. Gọi M,N lần lượt là trung điểm câc các cạnh AA';CD. Tính cosin góc giữa hai đường thẳng MN và B'C?

    Hình vẽ minh họa

    Gọi P là trung điểm của DC’. Ta có: \left\{ \begin{matrix} A'D//B'C \\ MN//A'P \\ \end{matrix} ight.

    Suy ra (MN,B'C) = (A'P,A'D) = \widehat{DA'P}

    Xét tam giác ADA’ có \left\{ \begin{matrix} AD = AA' \\ \widehat{DAA'} = 60^{0} \\ \end{matrix} ight. suy ra tam giác ADA’ là tam giác đều \Rightarrow A'D = x

    Xét tam giác A’AB có \left\{ \begin{matrix} AB = AA' \\ \widehat{A'AB} = 60^{0} \\ \end{matrix} ight. suy ra tam giác A’AB đều

    Do đó tam giác DD’C đều

    Vậy DC' = 2DP = 2.\frac{x\sqrt{3}}{2}= x\sqrt{3}

    Xét tam giác BAD có AD = AB và \widehat{BAD} = 60^{0} nên tam giác BAD là tam giác đều.

    Vì tam giác BAD đều nên tam giác B’A’D’ cùng là tam giác đều.

    Gọi A’I là đường cao của tam giác B’A’D’

    Khi đó: A'C' = 2A'I =2.\frac{x\sqrt{2}}{2} = x\sqrt{3}

    Dễ thấy A’P là đường trung tuyến của tam giác DA’C’ nên A'P = \sqrt{\frac{A'D'^{2} +A'C'^{2}}{2} - \frac{DC'^{2}}{4}} =\frac{x\sqrt{5}}{2}

    Áp dụng định lí cosin cho tam giác A’DP có:

    \Rightarrow \cos\widehat{DA'P} =\frac{A'D^{2} + A'P^{2} - DP^{2}}{2.A'D.A'P} =\frac{x\sqrt{5}}{10}

    \Rightarrow \cos(MN,B'C) = \left| \cos\widehat{DA'P} ight| = \frac{3\sqrt{5}}{10}

  • Câu 32: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, SA ⊥ (ABCD). I là trung điểm của SC. Khẳng định nào dưới đây sai?

    Hình vẽ minh họa:

    Ta có: O và I lần lượt là trung điểm của AC và SC

    => OI là đường trung bình của tam giác SAC

    => OI // SA

    Mà SA ⊥ (ABCD) => OI ⊥ (ABCD)

    Ta có: ABCD là hình chữ nhật => BC ⊥ AB

    Mà SA ⊥ BC => BC ⊥ SB

    Tương tự ta có: CD ⊥ AD, CD ⊥ SA => CD ⊥ SD

    Nếu (SAC) là mặt phẳng trung trực của BD => BD ⊥ AC điều này không thể xảy ra vì ABCD là hình chữ nhật.

    Vậy khẳng định sai là: “Mặt phẳng (SAC) là mặt phẳng trung trực của BD.”

  • Câu 33: Nhận biết

    Cho hai đường thẳng phân biệt a, b và mặt phẳng (P) trong đó a ⊥ (P). Chọn mệnh đề sai trong các mệnh đề dưới đây.

    Mệnh đề sai: “Nếu a ⊥ b thì b // (P).”

    Vì b có thể nằm trong (P).

  • Câu 34: Nhận biết

    Cho một khối chóp có diện tích đáy bằng 3a^{2}, chiều cao bằng a. Thể tích khối chóp đã cho là:

    Ta có: \left\{ \begin{matrix} B = 3a^{2} \\ h = a \\ \end{matrix} ight.

    Thể tích khối chóp là: V = \frac{1}{3}B.h = a^{3}

  • Câu 35: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông, đường chéo AC = 2a và SA vuông góc với mặt phẳng đáy (ABCD) (tham khảo hình vẽ). Tính khoảng cách giữa hai đường thẳng SB và CD.

    Hình vẽ minh họa:

    Vì AB // CD ⇒ CD // (SAB)

    => d(CD, (SAB)) = d(D, (SAB))

    Mà AD ⊥ (SAB) => d(D, (SAB)) = AD.

    Xét tam giác ABD vuông tại A ta có:

    AB2 + AD2 = BD2 = 4a2 => AD = a\sqrt{2}

  • Câu 36: Nhận biết

    Cho tứ diện ABCD có đáy BCD là tam giác vuông cân tại C. Gọi trung điểm các cạnh AB,AC,BC,CD lần lượt là M,N,P,Q. Khi đó (MN,PQ) bằng:

    Hình vẽ minh họa

    Ta có: \left\{ \begin{matrix} MN//BC \\ PQ//BD \\ \end{matrix} ight.

    \Rightarrow (MN,PQ) = (BC,BD) = \widehat{DBC} = 45^{0}

  • Câu 37: Thông hiểu

    Cho hình lập phương ABCD.A'B'C'D' có các cạnh bằng 1. Tính khoảng cách giữa hai mặt phẳng (ABB') và (CC'D').

    Hình vẽ minh họa

    Vì ABCD.A'B'C'D' là hình lập phương nên (ABB')//(CC'D') và BC\bot(ABB'A').

    Khoảng cách giữa hai mặt phẳng (ABB') và (CC'D')

    d\left( (ABB'),(CC'D') ight) = d\left( C,(ABB'A') ight) = CB = 1

  • Câu 38: Nhận biết

    Cho hình chóp S.ABC, tam giác ABC vuông tại B, cạnh bên SA vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SB (tham khảo hình vẽ bên). Mệnh đề nào sau đây sai?

    Ta có: SA ⊥ (ABC) => SA ⊥ BC

    Mặt khác BC ⊥ AB

    Suy ra BC ⊥ (SAB) nên hình chiếu vuông góc của SC trên (SAB) là SB

    Vậy \widehat{\left( SC,(SAB) ight)} =\widehat{(SC,SB)} = \widehat{BSC\ }(vì tam giác SBC vuông tại B)

  • Câu 39: Vận dụng

    Cho lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh đều bằng a. Khoảng cách giữa hai đường thẳng BC và AB’ bằng:

    Hình vẽ minh họa:

    Ta có BC // B’C’ => BC // (AB’C’)

    => d(BC, AB’) = d(BC, (AB’C’)) = d(B, (AB’C’)) = d(A’ ,(AB’C’))

    Gọi I và H lần lượt là hình chiếu vuông góc của A’ trên B’C’ và AI

    Ta có: B’C’⊥ A’I và B’C’⊥ A’A nên B’C’⊥ (A’AI) => B’C’⊥ A’H

    Mà AI ⊥ A’H

    => (AB’C’) ⊥ A’H.

    Khi đó:

    d\left( A';(AB'C') ight) =A'H = \frac{AA'.A'I}{\sqrt{AA'^{2} +A'I^{2}}}

    =\dfrac{a.\dfrac{a\sqrt{3}}{2}}{\sqrt{a^{2} + \left( \dfrac{a\sqrt{3}}{2}ight)^{2}}} = \dfrac{a\sqrt{21}}{7}

    Vậy khoảng cách cần tìm là \frac{a\sqrt{21}}{7}

  • Câu 40: Nhận biết

    Đường thẳng a vuông góc với hai đường thẳng phân biệt trong mặt phẳng (P) thì:

    "a vuông góc với mặt phẳng (P)" sai vì có thể có trường hợp

    a ⊥ b ⊂ (P); a⊥c ⊂ (P); b // c

    "a không vuông góc với mặt phẳng (P)" sai vì có thể xảy ra trường hợp

    a ⊥ b ⊂ (P); a⊥ c ⊂ (P); b ∩ c ≠ ∅

    =>a⊥(P)

    => "a không thể vuông góc với mặt phẳng (P)" là sai.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Toán 11 Chương 8 Cánh Diều Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án
Làm lại
  • 9 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề kiểm tra 45 phút Toán 11 Chương 8 Cánh Diều
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập