Xác định tập nghiệm của phương trình ![]() ?
?
Điều kiện xác định:
Phương trình đã cho tương đương:
Vậy phương trình có tập nghiệm là
Xác định tập nghiệm của phương trình ![]() ?
?
Điều kiện xác định:
Phương trình đã cho tương đương:
Vậy phương trình có tập nghiệm là
Cho tứ diện đều ABCD. Số đo góc giữa hai đường thẳng AB và CD là:
Gọi a là độ dài cạnh tứ diện. Khi đó
Cho biết ![]() . Một học sinh đã thực hiện tính giá trị biểu thức
. Một học sinh đã thực hiện tính giá trị biểu thức ![]() như sau:
như sau:
Bước 1: ![]()
Bước 2: ![]()
Bước 3: ![]()
Bước 4: ![]()
Hỏi bạn học sinh giải toán sai từ bước nào?
Ta có:
Vậy bài toán sai từ bước 4.
Cho hình chóp tứ giác ![]() có đáy
có đáy ![]() là hình chữ nhật, cạnh bên
là hình chữ nhật, cạnh bên ![]() vuông góc với mặt phẳng đáy. Gọi
vuông góc với mặt phẳng đáy. Gọi ![]() lần lượt là hình chiếu vuông của
lần lượt là hình chiếu vuông của ![]() lên
lên ![]() . Kết luận nào sau đây đúng?
. Kết luận nào sau đây đúng?
Hình vẽ minh họa
Ta có:
Lại có:
Trong các hàm số sau đây, hàm số nào nghịch biến trên tập số thực ![]() ?
?
Hàm số là hàm số mũ có cơ số bằng
nghịch biến trên
.
Hàm số là hàm số mũ có cơ số
nên đồng biến trên
.
Hàm số chỉ xác định trên
.
Hàm số có
nên nghịch biến trên
.
Cho hình chóp ![]() có đáy
có đáy ![]() là hình chữ nhật và
là hình chữ nhật và ![]() vuông góc với mặt phẳng đáy. Gọi
vuông góc với mặt phẳng đáy. Gọi ![]() . Xác định
. Xác định ![]() ?
?
Hình vẽ minh họa
Ta có: Hình chiếu của SD lên mặt phẳng (ABCD) là AD nên góc giữa SD và mặt phẳng đáy là góc
Một người gửi vào ngân hàng 200 triệu đồng vào tài khoản tiết kiệm ngân hàng với lãi suất 0,6%/ tháng, cứ sau mỗi tháng người đó rút ra 500 nghìn đồng. Hỏi sau đúng 36 lần rút tiền thì số tiền còn lại trong tài khoản của người đó gần nhất với phương án nào sau đây? (Biết rằng lãi suất không thay đổi và tiền lại mỗi tháng tính theo số tiền thực tế trong tài khoản của tháng đó?
Số tiền còn lại trong tài khoản sau tháng thứ 1 là: (triệu đồng)
Số tiền còn lại trong tài khoản sau tháng thứ 2 là:
(triệu đồng)
Số tiền còn lại trong tài khoản sau tháng thứ 3 là:
(triệu đồng)
Cứ tiếp tục quá trình thì số tiền còn lại trong tài khoản sau tháng thứ 36 là:
(triệu đồng).
Tập xác định của hàm số ![]() là:
là:
Hàm số xác định nếu
Vậy tập xác định .
Chọn phát biểu đúng trong các phát biểu dưới đây?
Phát biểu đúng là: “Nếu hàm số y = f(x) có đạo hàm tại m thì nó liên tục tại điểm đó.”
Tìm giá trị tham số m để bất phương trình ![]() có nghiệm đúng với mọi x.
có nghiệm đúng với mọi x.
Ta có:
Bất phương trình đã cho có nghiệm đúng với mọi x khi cả (1) và (2) đúng với mọi x.
Với hoặc
không thỏa mãn đề bài.
Với hoặc
để thỏa mãn đề bài thì:
Cho số thực dương a và b. Biểu thức thu gọn của biểu thức
![]()
có dạng ![]() . Tính
. Tính ![]() .
.
Ta có:
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và ![]() , CD = a. Gọi E là trung điểm của AD. Tính góc giữa hai đường thẳng AB và CE.
, CD = a. Gọi E là trung điểm của AD. Tính góc giữa hai đường thẳng AB và CE.
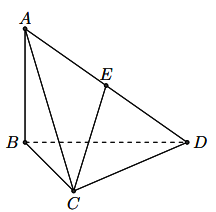
Kí hiệu hình vẽ như sau:
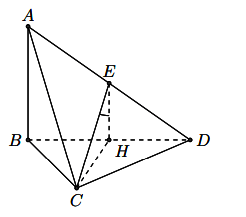
Gọi H là trung điểm của BD. Khi đó EH // AB, EH ⊥ (BCD)
Góc giữa AB và CE bằng góc giữa EH và EC chính là góc
Ta có:
Ta lại có:
Vậy góc giữa AB và CE là 450
Với ![]() là một số thực dương, biểu thức
là một số thực dương, biểu thức ![]() có giá trị là:
có giá trị là:
Ta có:
NB
Với a, b là các số thực dương tùy ý và a khác 1, đặt ![]() . Mệnh đề nào dưới đây đúng?
. Mệnh đề nào dưới đây đúng?
Ta có:
Thực hiện thu gọn biểu thức ![]() với
với ![]() ta được kết quả là:
ta được kết quả là:
Ta có:
Ta cũng có:
Khi đó:
Tính tỉ số ![]() của hàm số
của hàm số ![]() theo x và
theo x và ![]()
Ta có:
Cho x là số thực dương. Biết rằng ![\sqrt{x\sqrt[3]{x\sqrt{x\sqrt[3]{x}}}} =
x^{\frac{m}{n}}](https://i.khoahoc.vn/data/image/holder.png) với
với ![]() là các số tự nhiên và
là các số tự nhiên và ![]() là phân số tối giản. Chọn khẳng định đúng?
là phân số tối giản. Chọn khẳng định đúng?
Ta có:
Với số thực dương ![]() bất kì ta có
bất kì ta có ![]() tương ứng với:
tương ứng với:
Với ta có:
Cho hình hộp ![]() có đáy là hình thoi. Gọi mặt phẳng
có đáy là hình thoi. Gọi mặt phẳng ![]() chứa cạnh
chứa cạnh ![]() và cắt
và cắt ![]() lần lượt tại
lần lượt tại ![]() . Chọn kết luận đúng?
. Chọn kết luận đúng?
Hình vẽ minh họa
Ta có:
mà
Mặt khác
.
Cho hình chóp ![]() có đáy là hình vuông cạnh
có đáy là hình vuông cạnh ![]() và
và ![]() . Số đo góc giữa đường thẳng
. Số đo góc giữa đường thẳng ![]() và mặt phẳng
và mặt phẳng ![]() bằng:
bằng:
Hình vẽ minh họa
Ta có:
Mà nên SC là hình chiếu của SB lên mặt phẳng (SAB)
Góc giữa đường thẳng SC và mặt phẳng (SAB) là góc giữa SC và SB hay góc .
Trong tam giác SAB vuông tại A có
Trong tam giác SBC vuông tại B có
Số đo góc giữa đường thẳng và mặt phẳng
bằng
.
Xác định đạo hàm của hàm số ![]() .
.
Ta có:
Vậy
Tính vận tốc tức thời của chuyển động tại ![]() của một chất điểm chuyển động được xác định bởi phương trình
của một chất điểm chuyển động được xác định bởi phương trình ![]() , trong đó
, trong đó ![]() tính bằng giây và
tính bằng giây và ![]() được tính bằng mét.
được tính bằng mét.
Ta có:
Vận tốc tức thời của chuyển động khi là:
Tính số gia của hàm số ![]() tại điểm x0 ứng với số gia
tại điểm x0 ứng với số gia ![]()
Ta có:
Cho hình chóp ![]() ,
, ![]() vuông góc với mặt phẳng
vuông góc với mặt phẳng ![]() và
và ![]() . Hỏi có bao nhiêu mặt của hình chóp là tam giác vuông?
. Hỏi có bao nhiêu mặt của hình chóp là tam giác vuông?
Hình vẽ minh họa
Ta có: suy ra tam giác ABC vuông tại B
Ta có:
Suy ra tam giác SAB và tam giác SAC là các tam giác vuông tại A
Mặt khác suy ra tam giác SBC vuông tại B
Vậy hình chóp có bốn mặt đều là tam giác vuông.
Cho ![]() là các số thực dương bất kì. Mệnh đề nào dưới đây đúng?
là các số thực dương bất kì. Mệnh đề nào dưới đây đúng?
Ta có:
Cho hàm số ![]() có đạo hàm tại điểm
có đạo hàm tại điểm ![]() . Tìm khẳng định đúng trong các khẳng định sau?
. Tìm khẳng định đúng trong các khẳng định sau?
Theo định nghĩa đạo hàm ta có:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Gọi α là góc giữa đường thẳng SD và mặt phẳng (ABCD). Mệnh đề nào sau đây là mệnh đề đúng?
Hình vẽ minh họa:
Giả sử H là trung điểm của AB => SH ⊥ AB => SH ⊥ (ABCD)
=> Hình chiếu vuông góc của SD trên mặt phẳng (ABCD) là cạnh HD.
=>
Tam giác SAB đều cạnh a =>
Ta lại có:
=>
Tính giá trị biểu thức ![]() với
với ![]() ?
?
Ta có:
Biết ![]() với
với ![]() . Hỏi giá trị của biểu thức
. Hỏi giá trị của biểu thức ![]() bằng bao nhiêu?
bằng bao nhiêu?
Ta có:
Phương trình ![]() có bao nhiêu nghiệm?
có bao nhiêu nghiệm?
Ta có:
Logarit cơ số 7 hai vế ta có:
Giải phương trình ta được
Giải phương trình
Vậy tập nghiệm của phương trình là:
Chọn mệnh đề đúng?
Mệnh đề đúng: “Cho đường thẳng , mọi mặt phẳng
thì
”.
Minh họa bằng hình vẽ:
Cho hàm số ![]() . Tính
. Tính ![]() ?
?
Ta có:
Hàm số nào dưới đây đồng biến trên ![]() ?
?
Ta có: nên hàm số
đồng biến trên
.
Tính đạo hàm của hàm số ![]() trên khoảng
trên khoảng ![]() ?
?
Trên khoảng ta có:
Cho tứ diện đều ABCD. I là trung điểm của AB. Góc giữa hai đường thẳng IC và AD có cosin bằng:
Hình vẽ minh họa:
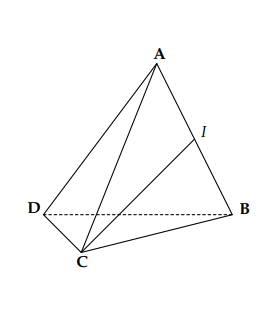
Giả sử cạnh tứ diện đều bằng a. Khi đó:
Ta có:
Tập nghiệm của bất phương trình ![]() là:
là:
Ta có:
hay
Tìm nghiệm phương trình ![]() ?
?
Điều kiện
Ta có:
Vậy phương trình có nghiệm .
Cho hình chóp ![]() có đáy là hình chữ nhật. Gọi trung điểm các cạnh
có đáy là hình chữ nhật. Gọi trung điểm các cạnh ![]() lần lượt là
lần lượt là ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Hình vẽ minh họa
Ta có: MN là đường trung bình của tam giác SCD =>
Ta có:
Cho hàm số ![]() . Tính đạo hàm của hàm số tại
. Tính đạo hàm của hàm số tại ![]() ?.
?.
Ta có:
Đặt
Khi đó:
Cho hai hàm số ![]() với
với ![]() là các số thực dương khác có đồ thị hàm số lần lượt là
là các số thực dương khác có đồ thị hàm số lần lượt là ![]() như hình vẽ.
như hình vẽ.

Chọn khẳng định đúng trong các khẳng định dưới đây.
Từ hình vẽ ta thấy đồ thị tăng suy ra hàm số
có cơ số
.
Đồ thị giảm suy ra hàm số
có cơ số
