Với giá trị nào của tham số a thì phương trình: ![]() có đúng hai nghiệm phân biệt.
có đúng hai nghiệm phân biệt.
.
Phương trình có hai nghiệm phân biệt ⇔ 1 ≤ a < 4.
Với giá trị nào của tham số a thì phương trình: ![]() có đúng hai nghiệm phân biệt.
có đúng hai nghiệm phân biệt.
.
Phương trình có hai nghiệm phân biệt ⇔ 1 ≤ a < 4.
Trong khai triển nhị thức Newton của ![]() , số hạng thứ hai theo số mũ tăng dần của biến
, số hạng thứ hai theo số mũ tăng dần của biến ![]() là:
là:
Ta có:
Tập nghiệm của phương trình  là?
là?
Điều kiện: .
Ta có: . Loại
.
Vậy .
Một nhóm học sinh gồm ![]() học sinh nam và
học sinh nam và ![]() học sinh nữ. Hỏi có bao nhiêu cách sắp xếp
học sinh nữ. Hỏi có bao nhiêu cách sắp xếp ![]() học sinh trên thành
học sinh trên thành ![]() hàng dọc sao cho nam nữ đứng xen kẽ?
hàng dọc sao cho nam nữ đứng xen kẽ?
Xếp học sinh nam thành hàng dọc có
cách xếp.
Giữa học sinh nam có
khoảng trống ta xếp các bạn nữ vào vị trí đó nên có
cách xếp.
Theo quy tắc nhân có cách xếp thoả mãn.
Tam thức nào sau đây nhận giá trị không âm với mọi x ∈ ℝ?
*x2 − x − 5 = 0 có 2 nghiệm phân biệt
* − x2 − x − 1 = 0vô nghiệm, a = − 1 < 0 nên − x2 − x − 1 < 0, ∀x ∈ ℝ
*2x2 + x = 0 có 2 nghiệm phân biệt
*x2 + x + 1 = 0 vô nghiệm, a = 1 > 0 nên x2 + x + 1 > 0, ∀x ∈ ℝ thỏa ycbt.
Hỏi có bao nhiêu giá trị nguyên của x thỏa mãn bất phương trình ![]() ?
?
Bất phương trình
Vì x2 ≥ 0, ∀x ∈ ℝ nên bất phương trình
Phương trình và
Bảng xét dấu
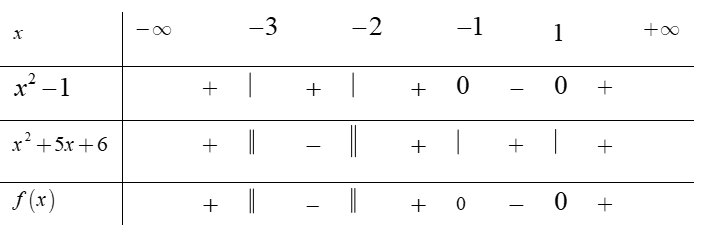
Dựa vào bảng xét dấu, ta thấy f(x) ≤ 0 ⇔ x ∈ (−3 ; −2) ∪ [ − 1 ; 1].
Kết hợp với x ∈ ℤ ta được x = {−1 ; 0 ; 1}.
Vậy có tất cả 3 giá trị nguyên cần tìm.
Một người có 5 chiếc áo trong đó có ![]() chiếc áo trắng. Người đó cũng có 3 chiếc cà vạt trong đó có 2 chiếc cà vạt màu vàng. Tìm số cách chọn một chiếc áo và một chiếc cà vạt sao cho đã chọn áo trắng thì không chọn cà vạt màu vàng.
chiếc áo trắng. Người đó cũng có 3 chiếc cà vạt trong đó có 2 chiếc cà vạt màu vàng. Tìm số cách chọn một chiếc áo và một chiếc cà vạt sao cho đã chọn áo trắng thì không chọn cà vạt màu vàng.
5 chiếc áo gồm: 3 trắng và 2 màu khác.
3 chiếc cà vạt gồm: 2 vàng và 1 màu khác.
Trường hợp 1: Áo trắng, cà vạt màu khác vàng.
Áo trắng: có 3 cách chọn.
Cà vạt màu khác vàng: 1 cách chọn.
Suy ra có: 3.1 = 3 (cách).
Trường hợp 2: Áo màu khác trắng, cà vạt màu bất kì.
Áo màu khác trắng: 2 cách chọn.
Cà vạt màu bất kì: 3 cách chọn.
Suy ra có: 2.3 = 6 (cách).
Vậy có: 3+6 = 9 (cách) chọn thỏa mãn yêu cầu đề bài.
Phương trình ![]() có nghiệm là:
có nghiệm là:
Điều kiện:
Phương trình tương đương:
Kết hợp với điều kiện ra được: thỏa mãn điều kiện
Vậy phương trình có nghiệm
Tính góc tạo bởi giữa hai đường thẳng ![]() và
và ![]()
Ta có
Chọn mệnh đề sai? Đường thẳng ![]() được xác định khi biết
được xác định khi biết
Mệnh đề sai là: “một vectơ pháp tuyến hoặc một vectơ chỉ phương.”
Cho ![]() Tìm
Tìm ![]() biết
biết ![]() .
.
Ta có
Để
Số nghiệm của phương trình ![]() là bao nhiêu?
là bao nhiêu?
.
Vậy phương trình có hai nghiệm.
Trong hệ tọa độ ![]() , cho bốn điểm
, cho bốn điểm ![]() . Các điểm nào trong các điểm đã cho thẳng hàng với nhau?
. Các điểm nào trong các điểm đã cho thẳng hàng với nhau?
Ta có:
Vậy ba điểm thẳng hàng.
Trong mặt phẳng tọa độ ![]() , cho hình chữ nhật
, cho hình chữ nhật ![]() có điểm
có điểm ![]() . Gọi
. Gọi ![]() đối xứng với điểm
đối xứng với điểm ![]() qua
qua ![]() , điểm
, điểm ![]() là hình chiếu vuông góc của
là hình chiếu vuông góc của ![]() lên đường thẳng
lên đường thẳng ![]() . Biết rằng tọa độ điểm
. Biết rằng tọa độ điểm ![]() thuộc đường thẳng
thuộc đường thẳng ![]() . Khi đó:
. Khi đó:
Ta có: ADB’C là hình bình hành
Mà
Tam giác vuông cân tại I
là hình thang cân =>
đi qua điểm
và có vecto pháp tuyến
Phương trình CI:
Đội học sinh giỏi cấp trường môn Tiếng Anh của trường THPT X theo từng khối như sau: khối 10 có 5 học sinh, khối 11 có 5 học sinh và khối 12 có 5 học sinh. Nhà trường cần chọn một đội tuyển gồm 10 học sinh. Hỏi có bao nhiêu cách lập đội tuyển sao cho có học sinh cả 3 khối và có nhiều nhất 2 học sinh khối 10.
TH1. Có đúng 1 học sinh khối 10: (cách). (1 lớp 10 + 5 lớp 11 + 4 lớp 12 hoặc 1 lớp 10 + 5 lớp 12 + 4 lớp 11)
TH2. Có đúng 2 học sinh khối 10: (cách).
Có
cách lập đội tuyển sao cho có học sinh cả ba khối và có nhiều nhất 2 học sinh khối 10.
Cho hai điểm ![]() . Tọa độ trung điểm của đoạn AB là:
. Tọa độ trung điểm của đoạn AB là:
Gọi M là trung điểm của đoạn thẳng AB. Khi đó tọa độ điểm M là:
Cho hai đường thẳng ![]() và
và ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Ta có: suy ra
cắt
.
Vậy khẳng định đúng là: “ cắt
”.
Trong mặt phẳng tọa độ Oxy, cho hai điểm ![]() . Viết phương trình đường trung trực của đoạn thẳng
. Viết phương trình đường trung trực của đoạn thẳng ![]() ?
?
Gọi I là trung điểm của PQ, khi đó I(-2;4)
Đường trung trực của PQ đi qua điểm I và nhận làm vectơ pháp tuyến.
Phương trình đường trung trực của PQ là:
Vậy đường thẳng cần tìm là: .
Cặp bất phương trình nào sau đây là tương đương?
Ta có: .
Ta có: (Vì
với mọi giá trị
). Do đó
.
Trong mặt phẳng tọa độ ![]() cho tam giác
cho tam giác ![]() có
có ![]() và
và ![]() . Tính số đo góc
. Tính số đo góc ![]() của tam giác đã cho.
của tam giác đã cho.
Ta có: và
.
.
Giải phương trình ![]() . Kết luận nào sau đây đúng?
. Kết luận nào sau đây đúng?
Điều kiện:
Ta có:
Vậy kết luận đúng là: n là số nguyên tố.
Bảng xét dấu nào sau đây là bảng xét dấu của tam thức ![]() là:
là:
Xét biếu thức có
và nghiệm là
Ta có bảng xét dấu như sau:

Cho tam giác ABC. Tập hợp các điểm M thỏa mãn ![]() là:
là:
Ta có:
Vậy tập hợp các điểm M là đường thẳng đi qua A và vuông góc với BC.
Cho ![]() . Điều kiện để
. Điều kiện để ![]()
![]() là:
là:
Ta có:
.
Một đường thẳng có bao nhiêu vectơ chỉ phương?
Một đường thẳng có vô số vectơ chỉ phương.
Trong menu của một nhà hàng gồm 5 món mặn, 5 món tráng miệng và 3 loại nước uống. Thực khách đến ăn sẽ được lên thực đơn gồm 1 món mặn, 1 món tráng miệng và 1 loại nước uống. Số thực đơn có thể có là:
Chọn món mặn có 5 cách chọn.
Số cách chọn món tráng miệng là 5 cách.
Số cách chọn một loại nước uống là 3 cách.
Theo quy tắc nhân ta có: (cách).
Từ tập hợp các chữ số ![]() có thể lập được bao nhiêu số có ba chữ số đôi một khác nhau và luôn có mặt số 1?
có thể lập được bao nhiêu số có ba chữ số đôi một khác nhau và luôn có mặt số 1?
Gọi số tự nhiên có ba chữ số cần tìm có dạng
TH1: . Chọn b, c có 5.6 = 30 cách.
TH2: . Chọn b, c có 5.6 = 30 cách.
TH3: . Chọn b, c có 5.6 = 30 cách.
Vậy có thể lập được (số) thỏa mãn yêu cầu đề bài.
Trong mặt phẳng với hệ tọa độ ![]() , cho tam giác
, cho tam giác ![]() có
có ![]()
![]() và
và ![]() . Chiều cao của tam giác kẻ từ đỉnh
. Chiều cao của tam giác kẻ từ đỉnh ![]() bằng:
bằng:
Trong mặt phẳng với hệ trục tọa độ ![]() , cho hai đường thẳng
, cho hai đường thẳng ![]() và
và ![]() . Gọi điểm
. Gọi điểm ![]() sao cho
sao cho ![]() và
và ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() ?
?
Gọi
Khi đó:
Với
Với
Viết phương trình tham số của đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và vuông góc với đường thẳng
và vuông góc với đường thẳng ![]() ?
?
Vì nên vectơ chỉ phương của đường thẳng d là vectơ pháp tuyến của
Đường thẳng có vectơ pháp tuyến là:
và đi qua điểm
là:
.
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn ![]() là:
là:
Ta có: (I là trung điểm của BC)
=> Qũy tích điểm M là đường tròn đường kính IA.
Số tập hợp con có 3 phần tử của một tập hợp có 7 phần tử là:
Số tập hợp con cần tìm là số tổ hợp chập 3 của 7 phần tử.
Vậy có tập con cần tìm.
Cho tam giác ![]() cân tại
cân tại ![]() có phương trình đường thẳng BC:
có phương trình đường thẳng BC: ![]() và phương trình đường thẳng
và phương trình đường thẳng ![]() :
: ![]() . Phương trình đường thẳng
. Phương trình đường thẳng ![]() có dạng
có dạng ![]() và
và ![]() là phân số tối giản. Biết rằng đường thẳng
là phân số tối giản. Biết rằng đường thẳng ![]() đi qua điểm
đi qua điểm ![]() . Chọn kết luận đúng?
. Chọn kết luận đúng?
Đường thẳng AC: , đường thẳng AC có một vecto pháp tuyến là
.
Đường thẳng AB, BC lần lượt có một vecto pháp tuyến là:
Vì
Xét tam giác ABC cân tại A ta có:
vì
, chọn
suy ra
Vậy kết luận đúng là:
Trong mặt phẳng tọa độ ![]() , tọa độ vecto
, tọa độ vecto ![]() là:
là:
Ta có: .
Biểu thức ![]() là khai triển của nhị thức nào dưới đây?
là khai triển của nhị thức nào dưới đây?
Ta có:
Trong mặt phẳng tọa độ ![]() cho ba điểm
cho ba điểm ![]() Tính tích vô hướng
Tính tích vô hướng ![]()
Ta có: ,
Trong mặt phẳng tọa độ ![]() , cho hai vecto
, cho hai vecto ![]() và
và ![]() . Tính
. Tính ![]() ?
?
Theo bài ra ta có:
và
Khi đó:
Khoảng cách từ điểm ![]() đến đường thẳng
đến đường thẳng ![]() bằng:
bằng:
Áp dụng công thức tính khoảng cách từ một điểm đến một đường thẳng ta có:
Vậy khoảng cách từ điểm A đến đường thẳng đã cho bằng 1.
Tam thức bậc hai ![]()
Ta có: và
.
Phương trình có hai nghiệm là
và
.
Do đó
.
Số cách chọn một học sinh trong nhóm gồm 5 nữ và 4 nam là:
Áp dụng quy tắc cộng ta có số cách chọn một học sinh là: 5 + 4 = 9 cách.
