Lớp 12 Toán 12 - Chân trời sáng tạo

Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo Đề 2

Mời các bạn học cùng thử sức với đề Đề thi giữa học kì 1 môn Toán lớp 12 sách Chân trời sáng tạo nha!

  • Thời gian làm: 90 phút
  • Số câu hỏi: 22 câu
  • Số điểm tối đa: 22 điểm
Mua gói để Làm bài
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
  • Câu 1: Nhận biết

    Trong các hàm số sau, hàm số nào nghịch biến trên từng khoảng xác định?

    Xét hàm số y = \frac{2x + 1}{x - 3} ta có:

    Điều kiện xác định D\mathbb{= R}\backslash\left\{ 3 ight\}

    Lại có: y' = \frac{- 7}{(x - 3)^{2}} < 0;\forall x \in D nên hàm số y = \frac{2x + 1}{x - 3} nghịch biến trên từng khoảng xác định của nó.

  • Câu 2: Nhận biết

    Cho hàm số y = f(x) có đạo hàm f'(x) = (x - 1)^{2}(x + 2)(3 - x). Mệnh đề nào sau đây đúng?

    Xét f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 2 \\ x = 3 \\ \end{matrix} ight. ta có bảng xét dấu f'(x) như sau:

    Dựa vào bảng xét dấu ta thấy hàm số nghịch biến trên các khoảng ( - \infty; - 2);(3; + \infty), hàm số đồng biến trên khoảng ( - 2;3).

  • Câu 3: Thông hiểu

    Cho hàm số y = f(x) có đạo hàm f'(x) xác định và liên tục trên \mathbb{R}. Hình vẽ sau đây là đồ thị của hàm số y = f'(x):

    Hàm số g(x) = f\left( x - x^{2} ight) nghịch biến trên khoảng:

    Ta có:

    g'(x) = f'\left( x - x^{2} ight).(1 - 2x)

    g'(x) = 0 \Leftrightarrow f'\left( x - x^{2} ight).(1 - 2x) = 0

    \Leftrightarrow \left\lbrack \begin{matrix} f'\left( x - x^{2} ight) = 0 \\ 1 - 2x = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x - x^{2} = 1 \\ x - x^{2} = 2 \\ 1 - 2x = 0 \\ \end{matrix} ight.\ \Leftrightarrow x = \frac{1}{2}

    Với x = 0 ta có: g'(0) = f'\left( 0 - 0^{2} ight).(1 - 2.0) = 2 > 0 ta có bảng xét dấu của g'(x) như sau:

    Suy ra hàm số g(x) nghịch biến trên khoảng \left( \frac{1}{2}; + \infty ight).

  • Câu 4: Nhận biết

    Cho hàm số y = x^{4} - x^{3} + 3. Khẳng định nào sau đây đúng?

    Ta có: y' = 4x^{3} - 3x^{2} = 0\Leftrightarrow \left\lbrack \begin{matrix}x = 0 \\x = \dfrac{3}{4} \\\end{matrix} ight.

    Ta có bảng xét dấu như sau:

    Vậy hàm số có đúng một cực trị.

  • Câu 5: Nhận biết

    Cho hàm số y = f(x) liên tục trên đoạn \lbrack - 1;4brack và có đồ thị như hình vẽ:

    Giả sử M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \lbrack - 1;4brack. Khi đó giá trị của biểu thức S = M + m bằng bao nhiêu?

    Từ đồ thị hàm số y = f(x) liên tục trên \lbrack - 1;4brack

    \Rightarrow \left\{ \begin{matrix} M = 3 \\ m = - 1 \\ \end{matrix} ight.\ \Rightarrow S = M + m = 2

  • Câu 6: Nhận biết

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Đồ thị hàm số có đường tiệm cận đứng là:

    Từ bảng biến thiên ta có:

    \lim_{x ightarrow - 1^{-}}f(x) = + \infty;\lim_{x ightarrow - 1^{+}}f(x) = - \infty

    Suy ra đồ thị hàm số có tiệm cận đứng là đường thẳng x = - 1

  • Câu 7: Thông hiểu

    Số tiệm cận của đồ thị hàm số y = \frac{(2x - 1)\sqrt{x^{2} + 1}}{x^{2} - 1} là:

    Ta có:

    \lim_{x ightarrow + \infty}y = \lim_{xightarrow + \infty}\dfrac{\left( 2x^{2} - x ight)\sqrt{1 +\dfrac{1}{x^{2}}}}{x^{2} - 1}= \lim_{x ightarrow + \infty}\dfrac{\left(2 - \dfrac{1}{x} ight)\sqrt{1 + \dfrac{1}{x^{2}}}}{1 - \dfrac{1}{x^{2}}}= 2

    \lim_{x ightarrow - \infty}y = \lim_{x ightarrow - \infty}\frac{\left( - 2x^{2} + x ight)\sqrt{1 + \frac{1}{x^{2}}}}{x^{2} - 1} = \lim_{x ightarrow - \infty}\frac{\left( - 2 + \frac{1}{x} ight)\sqrt{1 + \frac{1}{x^{2}}}}{1 - \frac{1}{x^{2}}} = - 2

    Suy ra y = \pm 2 là tiệm cận ngang.

    \lim_{x ightarrow 1^{\pm}}y = \lim_{x ightarrow 1^{\pm}}\frac{(2x - 1)\sqrt{x^{2} + 1}}{x^{2} - 1} = \pm \infty suy ra x = 1 là tiệm cận đứng.

    \lim_{x ightarrow ( - 1)^{\pm}}y = \lim_{x ightarrow ( - 1)^{\pm}}\frac{(2x - 1)\sqrt{x^{2} + 1}}{x^{2} - 1} = \pm \infty suy ra x = - 1 là tiệm cận đứng.

    Vậy đồ thị hàm số có tất cả 4 đường tiệm cận.

  • Câu 8: Nhận biết

    Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ:

    Đồ thị hàm số bậc 4 có hệ số a >0 và có ba điểm cực trị nên ab <0.

    Suy ra hàm số tương ứng với đồ thị đã cho là y = x^{4} - 2x^{2}.

  • Câu 9: Thông hiểu

    Cho hàm số y = \frac{{ax + b}}{{cx + d}} có bảng biến thiên như hình vẽ. Hỏi hàm số đã cho là hàm số nào?

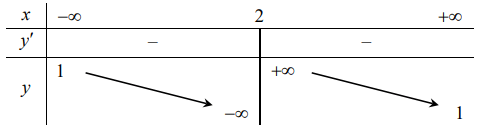
    Hàm số đã cho là hàm số nào

    Dựa vào bảng biến thiên ta thấy:

    Đồ thị hàm số nhận các đường thẳng x = 2 và tiệm cận ngang y = 1

    => Loại đáp án C và D

    Hàm số đã cho nghịch biến trên mỗi khoảng xác định

    Xét hàm số y = \frac{{x - 3}}{{x - 2}} \Rightarrow y' = \frac{1}{{{{\left( {x - 2} ight)}^2}}}

    => Hàm số đồng biến trên mỗi khoảng xác định nên ta loại đáp án A

  • Câu 10: Nhận biết

    Trong các mệnh đề sau, mệnh đề nào đúng?

    Nếu giá của ba vectơ cùng song song với một mặt phẳng thì ba vectơ đó đồng phẳng.

  • Câu 11: Nhận biết

    Cho tứ diện OABC. Gọi G là trọng tâm của tam giác ABC.Phân tích nào sau đây là đúng?

    Ta có: G là trọng tâm tam giác ABC khi \overrightarrow{OG} = \frac{1}{3}\left( \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} ight)

  • Câu 12: Nhận biết

    Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ dưới đây:

    Xét tính đúng sai của các khẳng định sau:

    a) Hàm số đồng biến trên khoảng (−2; 5). Sai|| Đúng

    b) Hàm số đạt cực đại tại điểm x = −2. Đúng||Sai

    c) Hàm số có giá trị nhỏ nhất bằng −2. Sai|| Đúng

    d) Hàm số có giá trị lớn nhất bằng 5. Đúng||Sai

    Đáp án là:

    Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ dưới đây:

    Xét tính đúng sai của các khẳng định sau:

    a) Hàm số đồng biến trên khoảng (−2; 5). Sai|| Đúng

    b) Hàm số đạt cực đại tại điểm x = −2. Đúng||Sai

    c) Hàm số có giá trị nhỏ nhất bằng −2. Sai|| Đúng

    d) Hàm số có giá trị lớn nhất bằng 5. Đúng||Sai

    Hàm số y = f(x) không có giá trị nhỏ nhất nên phát biểu “Hàm số y = f(x) có giá trị nhỏ nhất bằng −2” là phát biểu sai.

  • Câu 13: Thông hiểu

    Cho hàm số y = f(x) có: \lim_{x ightarrow 3^{-}}f(x) = 1;\lim_{xightarrow 3^{+}}f(x) = + \infty;\lim_{x ightarrow - \infty}f(x) =1;\lim_{x ightarrow + \infty}f(x) = + \infty

    Xét tính đúng sai của các khẳng định sau:

    a) Đồ thị của hàm số y = f(x) có tiệm cận ngang là đường thẳng y = 1. Đúng||Sai

    b) Đồ thị của hàm số y = f(x) có tiệm cận đứng là đường thẳng x = 3. Đúng||Sai

    c) Đồ thị của hàm số y = f(x) không có tiệm cận ngang. Sai|| Đúng

    d) Đồ thị của hàm số y = f(x) không có tiệm cận đứng. Sai|| Đúng

    Đáp án là:

    Cho hàm số y = f(x) có: \lim_{x ightarrow 3^{-}}f(x) = 1;\lim_{xightarrow 3^{+}}f(x) = + \infty;\lim_{x ightarrow - \infty}f(x) =1;\lim_{x ightarrow + \infty}f(x) = + \infty

    Xét tính đúng sai của các khẳng định sau:

    a) Đồ thị của hàm số y = f(x) có tiệm cận ngang là đường thẳng y = 1. Đúng||Sai

    b) Đồ thị của hàm số y = f(x) có tiệm cận đứng là đường thẳng x = 3. Đúng||Sai

    c) Đồ thị của hàm số y = f(x) không có tiệm cận ngang. Sai|| Đúng

    d) Đồ thị của hàm số y = f(x) không có tiệm cận đứng. Sai|| Đúng

    a) Do \lim_{x ightarrow - \infty}f(x) = 1 nên y = 1 là đường tiệm cận ngang của đồ thị hàm số. (*)

    b) Do \lim_{x ightarrow 3^{+}}f(x) = + \infty nên x = 3 là đường tiệm cận đứng của đồ thị hàm số. (**)

    c) Từ (*) suy ra khẳng định này sai.

    d) Từ (**) suy ra khẳng định này sai.

  • Câu 14: Thông hiểu

    Cho hàm số y = \frac{ax^{2} + bx + c}{ex + f} có đồ thị (C) như hình vẽ:

    Xét tính đúng sai của các khẳng định sau:

    a) Hàm số đồng biến trên (−∞; −1). Sai||Đúng

    b) Hàm số đạt cực đại tại x = −2. Sai||Đúng

    c) Giá trị nhỏ nhất của hàm số trên (−∞; −1) là \frac{3}{2}. Đúng||Sai

    d) Điểm cực tiểu của hàm số là x = −2. Đúng||Sai

    Đáp án là:

    Cho hàm số y = \frac{ax^{2} + bx + c}{ex + f} có đồ thị (C) như hình vẽ:

    Xét tính đúng sai của các khẳng định sau:

    a) Hàm số đồng biến trên (−∞; −1). Sai||Đúng

    b) Hàm số đạt cực đại tại x = −2. Sai||Đúng

    c) Giá trị nhỏ nhất của hàm số trên (−∞; −1) là \frac{3}{2}. Đúng||Sai

    d) Điểm cực tiểu của hàm số là x = −2. Đúng||Sai

    a) Sai. Hàm số đồng biến trên (−2; −1), (−1; 0) và nghịch biến trên (−∞; −2), (0; +∞).

    b) Sai. Hàm số đạt cực tiểu tại x = −2.

    c) Đúng.

    d) Đúng.

  • Câu 15: Vận dụng

    Cho tứ diện ABCD. Gọi M;N;P;Q;R;S;G lần lượt là trung điểm các đoạn thẳng AB;CD;AC;BD;AD;BC;MN.

    Xét tính đúng sai của các khẳng định sau.

    a) \overrightarrow{MR} = \overrightarrow{SN}. Sai||Đúng

    b) \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \overrightarrow{0}. Đúng||Sai

    c) 2\overrightarrow{PQ} = \overrightarrow{AB} + \overrightarrow{AC} + \overrightarrow{AD}. Sai||Đúng

    d) \left| \overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} + \overrightarrow{ID} ight| nhỏ nhất khi và chỉ khi điểm I trùng với điểm G. Đúng||Sai

    Đáp án là:

    Cho tứ diện ABCD. Gọi M;N;P;Q;R;S;G lần lượt là trung điểm các đoạn thẳng AB;CD;AC;BD;AD;BC;MN.

    Xét tính đúng sai của các khẳng định sau.

    a) \overrightarrow{MR} = \overrightarrow{SN}. Sai||Đúng

    b) \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \overrightarrow{0}. Đúng||Sai

    c) 2\overrightarrow{PQ} = \overrightarrow{AB} + \overrightarrow{AC} + \overrightarrow{AD}. Sai||Đúng

    d) \left| \overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} + \overrightarrow{ID} ight| nhỏ nhất khi và chỉ khi điểm I trùng với điểm G. Đúng||Sai

    Hình vẽ minh họa

    a) Đúng: \left. \ \begin{matrix}\overrightarrow{MR} = \dfrac{1}{2}\overrightarrow{BD} \\\overrightarrow{SN} = \dfrac{1}{2}\overrightarrow{BD} \\\end{matrix} ight\} \Rightarrow \overrightarrow{MR} =\overrightarrow{SN}.

    b) Đúng: Vi M là trung điểm của AB nên \overrightarrow{GA} + \overrightarrow{GB} = 2\overrightarrow{GM}

    Vì N là trung điểm của CD nên \overrightarrow{GC} + \overrightarrow{GD} = 2\overrightarrow{GN}

    Vì G là trung điểm của MN nên \overrightarrow{GM} + \overrightarrow{GN} = \overrightarrow{0}

    Do đó: \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = 2(\overrightarrow{GM} + \overrightarrow{GN}) = 2.\overrightarrow{0} = \overrightarrow{0}

    c) Sai: \overrightarrow{PQ} =\overrightarrow{AQ} - \overrightarrow{AP} =\frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AD}) -\frac{1}{2}\overrightarrow{AC}\Leftrightarrow 2\overrightarrow{PQ} =\overrightarrow{AB} - \overrightarrow{AC} +\overrightarrow{AD}

    d) Đúng

    Ta có: \overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} + \overrightarrow{ID} = 4\overrightarrow{IG} + (\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD}) = 4\overrightarrow{IG}.

    \Rightarrow |\overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} + \overrightarrow{ID}| = |4\overrightarrow{IG}| = 4IG.

    Do đó: |\overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} + \overrightarrow{ID}| nhỏ nhất khi IG = 0 \Leftrightarrow I \equiv G 

  • Câu 16: Thông hiểu

    Có bao nhiêu giá trị nguyên của tham số m để hàm số y = \frac{mx - 3}{2x - m} đồng biến trên từng khoảng xác định?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Có bao nhiêu giá trị nguyên của tham số m để hàm số y = \frac{mx - 3}{2x - m} đồng biến trên từng khoảng xác định?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 17: Vận dụng

    Cho hàm số y = f(x) = \left| x^{3} -3x^{2} + m ight| biết m \in\lbrack - 4;4brack. Có thể có bao nhiêu giá trị nguyên của tham số m để hàm số đã cho có đúng ba điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) = \left| x^{3} -3x^{2} + m ight| biết m \in\lbrack - 4;4brack. Có thể có bao nhiêu giá trị nguyên của tham số m để hàm số đã cho có đúng ba điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 18: Vận dụng

    Để uốn 4m thanh kim loại thành hình như sau:

    Gọi r bán kính của nửa đường tròn. Tìm r(m) để diện tích tạo thành đạt giá trị lớn nhất?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Để uốn 4m thanh kim loại thành hình như sau:

    Gọi r bán kính của nửa đường tròn. Tìm r(m) để diện tích tạo thành đạt giá trị lớn nhất?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 19: Vận dụng

    Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = \frac{\sqrt{1 - x}}{x^{2} + 4x + m} có đúng ba đường tiệm cận?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = \frac{\sqrt{1 - x}}{x^{2} + 4x + m} có đúng ba đường tiệm cận?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 20: Vận dụng

    Gọi M;N lần lượt là trung điểm của các cạnh AC;BD của tứ diện ABCD. Gọi I là trung điểm của đoạn MN. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ \overrightarrow{IA} + (2k - 1)\overrightarrow{IB}+ k\overrightarrow{IC} + \overrightarrow{ID} =\overrightarrow{0}?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Gọi M;N lần lượt là trung điểm của các cạnh AC;BD của tứ diện ABCD. Gọi I là trung điểm của đoạn MN. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ \overrightarrow{IA} + (2k - 1)\overrightarrow{IB}+ k\overrightarrow{IC} + \overrightarrow{ID} =\overrightarrow{0}?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 21: Vận dụng cao

    Có bao nhiêu giá trị nguyên của m \in\lbrack - 10;10brack để hàm số y= \left| x^{4} + 2mx^{3} + (3 - 3m)x^{2} - 2mx + 3m - 4 ight| có 7 điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Có bao nhiêu giá trị nguyên của m \in\lbrack - 10;10brack để hàm số y= \left| x^{4} + 2mx^{3} + (3 - 3m)x^{2} - 2mx + 3m - 4 ight| có 7 điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 22: Thông hiểu

    Cho hàm số y = f(x) = \frac{mx - 8}{2x - m} (với m là tham số). Tìm tất cả các giá trị của tham số m để hàm số đồng biến trên từng khoảng xác định?

    Tập xác định x eq \frac{m}{2}

    Ta có: y' = \frac{- m^{2} + 16}{(2x - m)^{2}}.

    Để hàm số đồng biến trên khoảng xác định thì y' > 0 \Leftrightarrow \frac{- m^{2} + 16}{(2x - m)^{2}} > 0

    \Leftrightarrow - m^{2} + 16 > 0 \Leftrightarrow - 4 < m < 4

    Vậy đáp án cần tìm là: - 4 < m < 4.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo Đề 2 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 6 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo Đề 2
Thời gian còn lại 90:00 Số câu đã làm 0/22
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập