Lớp 11 Toán 11 - Chân trời sáng tạo

Đề thi HK2 Toán 11 Chân trời sáng tạo - Đề 4

Mô tả thêm: Đề thi học kì 2 Toán 11 Chân trời sáng tạo gồm 40 câu hỏi trắc nghiệm khách quan, gồm 4 mức độ khác nhau giúp đánh giá đúng năng lực học tập.
  • Thời gian làm: 90 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Mua gói để Làm bài
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
  • Câu 1: Thông hiểu

    Cho P(A) = 0,5;P(B) = 0,4;P(AB) = 0,2. Chọn khẳng định đúng?

    Theo giả thiết ta có:

    P(A.B) = P(A).P(B)

    = 0,5.0,4 = 0,2 = P(AB)

    Vậy hai biến cố A và B là hai biến cố độc lập.

  • Câu 2: Nhận biết

    Trong các kết quả dưới đây, kết quả nào là tập nghiệm của bất phương trình \left( \frac{1}{3} ight)^{x} < 2?

    Ta có:

    \left( \frac{1}{3} ight)^{x} < 2 \Leftrightarrow x > log_{\frac{1}{3}}2

    Vậy tập nghiệm của bất phương trình đã cho là x \in \left(\log_{\frac{1}{3}}2; + \inftyight)

  • Câu 3: Nhận biết

    Gieo hai lần liên tiếp một đồng xu. Gọi M là biến cố có ít nhất một lần mặt sấp xuất hiện, N là biến cố kết quả hai lần gieo giống nhau. Chọn khẳng định đúng?

    Ta có:

    M = \left\{ SS;SN;NS ight\}

    N = \left\{ SS;NN ight\}

    \Rightarrow M \cup N = \left\{ SS;SN;NS;NN ight\}

  • Câu 4: Nhận biết

    Cho một khối chóp có diện tích đáy bằng 5a^{2}, chiều cao bằng a. Thể tích khối chóp đã cho là:

    Ta có: \left\{ \begin{matrix} B = 5a^{2} \\ h = a \\ \end{matrix} ight.

    Thể tích khối chóp là: V = \frac{1}{3}B.h = \frac{5}{3}a^{3}

  • Câu 5: Nhận biết

    Tung một đồng tiền xu cân đối và đồng chất 5 lần liên tiếp. Tính số phần tử của biến cố “Mặt sấp xuất hiện ít nhất 1 lần”.

    Số phần tử không gian mẫu là:

    n(\Omega) = 2^{5} = 32

    Gọi A là biến cố “Mặt sấp xuất hiện ít nhất 1 lần” khi đó \overline{A} là biến cố “Mặt sấp không xuất hiện”

    Khi đó \overline{A} = \left\{ NNNNN ight\} \Rightarrow n\left( \overline{A} ight) = 1

    Khi đó n(A) = 32 - 1 = 31

  • Câu 6: Nhận biết

    Đạo hàm của hàm số y = \log_{4}(2x + 5) là:

    Ta có:

    y = \log_{4}(2x + 5)

    \Rightarrow y' = \frac{2}{(2x +5)\ln4}

    = \frac{2}{(2x + 5).2.\ln2} =\frac{1}{(2x + 5).\ln2}

  • Câu 7: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA\bot(ABCD);SA = a\sqrt{2}. Tính khoảng cách giữa hai đường chéo nhau AC và SB bằng:

    Hình vẽ minh họa

    Kẻ đường thẳng d qua B và song song AC

    Gọi M là hình chiếu vuông góc của A lên d

    Gọi H là hình chiếu của A lên SM.

    Ta có: \left\{ \begin{matrix} SA\bot BM \\ BM\bot AM \\ \end{matrix} ight.\ \Rightarrow BM\bot(SAM) \Rightarrow AH\bot(SBM)

    \Rightarrow d(AC;SB) = d\left( A;(SBM) ight) = AH

    Xét tam giác SAM có đường cao AH nên

    \frac{1}{AH^{2}} = \frac{1}{AS^{2}} + \frac{1}{AM^{2}} = \frac{5}{2a^{2}}

    \Rightarrow AH = \frac{a\sqrt{10}}{5}

  • Câu 8: Thông hiểu

    Cho các mệnh đề sau:

    (i) Cơ số của logarit phải là số dương.

    (ii) Chỉ số thực dương mới có logarit.

    (iii) \ln(A + B) = \ln A + \lnB với mọi A > 0;B >0.

    (iv) \log_{a}b.\log_{b}c.\log_{c}a =1 với mọi a,b,c\in\mathbb{R}

    Số mệnh đề đúng là:

    (i) Sai vì cơ số của \log_{a}b chỉ cần thỏa mãn 0 < a eq0

    (ii) Đúng vì điều kiện có nghĩa của \log_{a}b là b> 0

    (iii) Sai vì \ln(A + B) = \ln A.\ln B với mọi A > 0;B >0.

    (iv) Sai vì nếu a,b,c < 0 thì các biểu thức \log_{a}b;\log_{b}c;\log_{c}a không có nghĩa.

  • Câu 9: Thông hiểu

    Cho hình chóp S.ABC có đáy ABC là hình tam giác vuông tại B, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi H;K lần lượt là hình chiếu của điểm A trên cạnh SB;SC. Kết luận nào sau đây sai?

    Hình vẽ minh họa

    Ta có: \left\{ \begin{matrix}SA\bot(ABC) \\BC \subset (ABC) \\\end{matrix} ight.\ \Rightarrow SA\bot BC;AB\bot BC

    \Rightarrow BC\bot(SAB) đúng

    Ta có: \left\{ \begin{matrix}BC\bot AH \\SC\bot AH \\\end{matrix} ight.\ \Rightarrow AH\bot(SBC) đúng

    Ta có: \left\{ \begin{matrix}AH\bot SC \\AK\bot SC \\\end{matrix} ight.\ \Rightarrow SC\bot(AHK) đúng

    Vậy kết luận sai là: AK\bot(SBC).

  • Câu 10: Nhận biết

    Tìm hàm số nghịch biến trên \mathbb{R} trong các hàm số sau?

    Ta có:

    0 < \sqrt{5} - 2 < 1 nên hàm số y = \left( \sqrt{5} - 2 ight)^{x} nghịch biến trên \mathbb{R}.

  • Câu 11: Thông hiểu

    Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh bằng 2\sqrt 2, AA’ = 4. Tính góc giữa đường thẳng A’C với mặt phẳng (AA’BB’).

     Số đo góc giữa đường thẳng A’C với mặt phẳng (AA’BB’)

    Ta có CB \bot \left( {AA'B'B} ight) tại B. Khi đó A’B là hình chiếu của A’C lên mặt phẳng (AA’B’B)

    Vậy góc tạo bởi đường thẳng A’C và mặt phẳng (AA’BB’) là góc \widehat {CA'B}

    Khi đó \tan \widehat {CA'B} = \frac{{BC}}{{A'B}} = \frac{{2\sqrt 2 }}{{\sqrt {{4^2} + {{\left( {2\sqrt 2 } ight)}^2}} }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {CA'B} = 30^\circ

  • Câu 12: Thông hiểu

    Học sinh A làm bài kiểm tra 15 phút môn Toán gồm 10 câu hỏi trắc nghiệm, mỗi câu hỏi gồm 4 phương án trả lời và chỉ có một phương án đúng. Nếu trả lời đúng 1 câu hỏi được 1 điểm, trả lời sai không có điểm. Biết A đã làm đúng 5 câu hỏi, vì thời gian hạn chế nên A đã khoanh trả lời ngẫu nhiên các câu hỏi còn lại. Tính xác suất để A đạt được ít nhất 8 điểm?

    Bạn A trả lời đúng 5 câu hỏi nên A đã đạt được 5 điểm

    Để được ít nhất 8 điểm thì A phải trả lời đúng ít nhất 3 câu trong 5 câu còn lại.

    TH1: 3 câu đúng, 2 câu sai P_{1} = C_{5}^{3}.\left( \frac{1}{4} ight)^{3}.\left( \frac{3}{4} ight)^{2}

    TH2: 4 câu đúng, 1 câu sai P_{2} = C_{5}^{4}.\left( \frac{1}{4} ight)^{4}.\left( \frac{3}{4} ight)^{1}

    TH3: 5 câu đúng P_{3} = C_{5}^{5}.\left( \frac{1}{4} ight)^{5}

    Vậy xác suất cần tìm là: P = P_{1} + P_{2} + P_{3} \approx 0,1035

  • Câu 13: Thông hiểu

    Cho hai hộp đựng các viên bi nhiều màu:

    Hộp 1 có 4 viên bi trắng, 5 viên bi đỏ và 6 viên bi xanh.

    Hộp 2 chứa 7 viên bi trắng, 6 viên bi đỏ và 5 viên bi xanh.

    Lấy ngẫu nhiên mỗi hộp 1 viên bi. Gọi A là biến cố “Hai viên bi lấy ra cùng màu”. Tính P(A)?

    Giả sử A_{1} là biến cố hai viên bi lấy được cùng màu trắng

    Khi đó P\left( A_{1} ight) = \frac{4}{15}.\frac{7}{18}

    A_{2} là biến cố hai viên bi lấy được cùng màu đỏ

    Khi đó P\left( A_{2} ight) = \frac{5}{15}.\frac{6}{18}

    A_{3} là biến cố hai viên bi lấy được cùng màu xanh

    Khi đó P\left( A_{3} ight) = \frac{6}{15}.\frac{5}{18}

    \Rightarrow P(A) = P\left( A_{1} ight) + P\left( A_{2} ight) + P\left( A_{3} ight) = \frac{44}{135}

  • Câu 14: Vận dụng

    Cho đồ thị của ba hàm số y = m^{x};y = n^{x};y = \log_{t}x như hình vẽ:

    Chọn kết luận đúng về mối quan hệ giữa m,n,t?

    Quan sát đồ thị ta thấy

    Hàm số y = m^{x} là hàm số đồng biến nên m > 1

    Hàm số y = n^{x} là hàm số đồng biến nên n > 1

    Hàm số y = \log_{t}x là hàm nghịch biến nên 0 < t < 1

    Vậy ta có: \left\{ \begin{matrix} 0 < t < m \\ 0 < t < n \\ \end{matrix} ight.

    Khi thay x = 1 vào hai hàm số y = m^{x};y = n^{x} ta thu được m > n

    Vậy t < n < m.

  • Câu 15: Nhận biết

    Thực hiện tung ngẫu nhiên một con xúc xắc một lần. Biết H là biến cố mặt xuất hiện có số chấm chẵn, K là biến cố mặt xuất hiện có số chấm lẻ. Khẳng định nào sau đây đúng?

    Vì \left\{ \begin{matrix}H \cap K = \varnothing \\H \cup K = \Omega \\\end{matrix} ight. nên hai biến cố H và K là hai biến cố đối nhau.

  • Câu 16: Vận dụng

    Cho tứ diện ABCD có các cạnh AB,AC,AD đôi một vuông góc với nhau. Gọi trung điểm của các cạnh BC,CD,DB lần lượt là J;Q;K. Tính thể tích tứ diện AJQK, biết AB = 6cm;AC = 7cm;AD = 4cm.

    Hình vẽ minh họa

    Ta có: V_{ABCD} =\frac{1}{2}AB.\frac{1}{2}AD.AC = \frac{1}{2}.6.7.4 = 28\left( cm^{3}ight)

    Nhận thấy S_{JQK} = \frac{1}{2}S_{JQKD} =\frac{1}{4}S_{BCD}

    V_{JQK} = \frac{1}{4}V_{ABCD} = 7\left(cm^{3} ight)

  • Câu 17: Nhận biết

    Cho hàm số y = f(x) xác định trên tập số thực thỏa mãn \lim_{x ightarrow 3}\frac{f(x) - f(3)}{x - 3} = 2. Chọn khẳng định đúng?

    Hàm số y = f(x) có đạo hàm tại điểm x_{0}

    f'\left( x_{0} ight) = \lim_{x ightarrow x_{0}}\frac{f(x) - f\left( x_{0} ight)}{x - x_{0}}

    Nên khẳng định đúng là f'(3) = 2

  • Câu 18: Nhận biết

    Cho hàm số f(x)=(x+10)^{6}. Tính giá trị của f''(2).

     Ta có:

    \begin{matrix} f(x) = {(x + 10)^6} \hfill \\ \Rightarrow f'\left( x ight) = 6.{\left( {x + 10} ight)^5} \hfill \\ \Rightarrow f''\left( x ight) = 6.5.{\left( {x + 10} ight)^4} = 30{\left( {x + 10} ight)^4} \hfill \\ \Rightarrow f''\left( 2 ight) = 622080 \hfill \\ \end{matrix}

  • Câu 19: Thông hiểu

    Một nhóm học sinh gồm 4 nam và 6 nữ. Chọn ngẫu nhiên 4 học sinh. Gọi M là biến cố 4 học sinh được chọn được có cả nam và nữ. Khi đó số phần tử của biến cố đối của A là:

    Ta có: \overline{M} là biến cố cả 4 bạn được chọn đều là nam hoặc 4 bạn đều là nữ.

    Do đó số phần tử của \overline{M} = C_{4}^{4} + C_{6}^{4} = 16

  • Câu 20: Vận dụng cao

    Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B; SAB là tam giác cân tại S; AD = 3BC = 3AB = 3a. Gọi M là điểm thuộc đoạn AD sao cho AD = 3MD. Biết rằng SCM là tam giác đều. Gọi α là góc giữa đường thẳng SB và mặt phẳng (SAD). Khi đó cos α nhận giá trị là

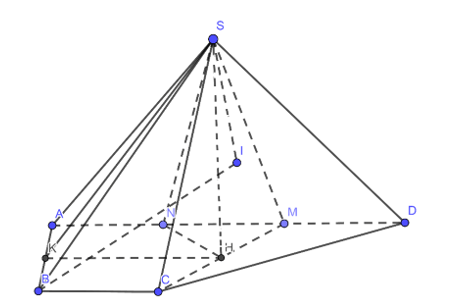
    Tính giá trị cos α

    Gọi K là trung điểm AB, N là trung điểm của AM, H là trung điểm của CM.

    Điểm M thuộc đoạn AD sao cho 3MD = AD = 3a

    => MD = a; AM = 2a

    Tam giác SAB cân tại A nên AB ⊥ SK.

    Vì HK là đường trung bình của hình thang vuông ABCM nên AB ⊥ HK và HK = \frac{{3a}}{2}

    Ta có: \left\{ \begin{gathered} AB \bot SK \hfill \\ AB \bot HK \hfill \\ \end{gathered} ight. \Rightarrow AB \bot SH (1)

    Tam giác SCM đều nên CM ⊥ SH (2)

    Từ (1) và (2) suy ra SH ⊥ (ABCD)

    Ta có AN = MN = MD = a nên ABCN là hình vuông, từ đó tam giác CMN vuông cân tại N.

    Suy ra HM = HN = \frac{1}{2}CM = \frac{{a\sqrt 2 }}{2} và HM \bot HN

    Tam giác SCM đều cạnh bằng a\sqrt 2 nên SH = \frac{{a\sqrt 6 }}{2}

    Tứ diện HSMN có HS, MN, HN đôi một vuông góc, đặt d = d(H, (SMN)).

    Ta có: \frac{1}{{{d^2}}} = \frac{1}{{H{M^2}}} + \frac{1}{{H{N^2}}} + \frac{1}{{H{S^2}}}

    = \frac{4}{{2{a^2}}} + \frac{4}{{2{a^2}}} + \frac{4}{{6{a^2}}} = \frac{{14}}{{3{a^2}}} \Rightarrow d = \frac{{a\sqrt {42} }}{{14}}

    Ta lại có:

    SB = \sqrt {S{H^2} + B{H^2}} = \sqrt {S{H^2} + B{K^2} + K{H^2}}

    = \sqrt {\frac{{3{a^2}}}{2} + \frac{{{a^2}}}{4} + \frac{{9{a^2}}}{4}} = 2a

    Gọi I là hình chiếu của điểm B trên mặt phẳng (SAD)

    Khi đó góc giữa đường thẳng SB và mặt phẳng (SAD) là góc \widehat {BSI} = \alpha

    Do BC // AD => BC //(SAD)

    => BI = d\left( {B;\left( {SAD} ight)} ight) = d\left( {C;\left( {SAD} ight)} ight) = 2d\left( {H,\left( {SAD} ight)} ight) = \frac{{a\sqrt {42} }}{7}

    Trong tam giác vuông BIS ta có:

    \sin \alpha = \frac{{BI}}{{SB}} = \frac{{\sqrt {42} }}{{14}} \Rightarrow \cos \alpha = \frac{{\sqrt {154} }}{{14}}

  • Câu 21: Nhận biết

    Cho hình chóp S.ABC, tam giác ABC vuông tại B, cạnh bên SA vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SB (tham khảo hình vẽ bên). Mệnh đề nào sau đây sai?

    Ta có: SA ⊥ (ABC) => SA ⊥ BC

    Mặt khác BC ⊥ AB

    Suy ra BC ⊥ (SAB) nên hình chiếu vuông góc của SC trên (SAB) là SB

    Vậy \widehat{\left( SC,(SAB) ight)} =\widehat{(SC,SB)} = \widehat{BSC\ }(vì tam giác SBC vuông tại B)

  • Câu 22: Thông hiểu

    Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a\sqrt{2}. Tính khoảng cách giữa hai đường thẳng CC’ và BD.

    Hình vẽ minh họa:

    Ta có:

    OC ⊥ BD

    OC ⊥ CC’

    => OC là đoạn vuông góc chung của CC’ và BD.

    Vậy d(CC’, BD) = OC = AC/2 = 2a/2 = a

  • Câu 23: Nhận biết

    Tung hai lần liên tiếp một đồng xu. Giả sử biến cố B là biến cố mặt sấp xuất hiện ít nhất một lần. Khi đó biến cố đối của biến cố B là:

    Biến cố đối của biến cố B là \overline{B}: “Mặt sấp không xuất hiện lần nào” nghĩa là mặt xuất hiện ở cả hai lần đều cho mặt ngửa”.

  • Câu 24: Thông hiểu

    Cho hình chóp S.ABCD có đáy là hình vuông với AC = 5\sqrt{2}. Biết SA\bot(ABCD);SA = 5. Góc giữa SD và mặt phẳng (SAB) bằng:

    Ta có: \left\{ \begin{matrix} AD\bot AB \\ AD\bot SA \\ \end{matrix} ight.\ \Rightarrow AD\bot(SAB)

    \Rightarrow \left( SD;(SAB) ight) = (SD;SA) = \widehat{DSA}

    Vì ABCD là hình vuông nên AC = AB.\sqrt{2} \Rightarrow AB = 5

    \Rightarrow \tan\widehat{DSA} = \frac{AD}{SA} = \frac{5}{5} = 1

    \Rightarrow \widehat{DSA} = 45^{0} \Rightarrow \left( SD;(SAB) ight) = 45^{0}

  • Câu 25: Nhận biết

    Với các số a, b, c là các số thực dương tùy ý khác 1 và \log_{a}c = x;\log_{b}c =y. Khi đó giá trị của \log_{a}(ab) bằng:

    Với a, b, c là các số thực dương tùy ý khác 1 ta có:

    \log_{c}a = \frac{1}{x};\log_{c}b =\frac{1}{y}

    Khi đó ta có: \log_{c}(ab) = \log_{c}a +\log_{c}b = \frac{1}{x} + \frac{1}{y}

  • Câu 26: Thông hiểu

    Cho hình chóp tứ giác đều S.ABCD, cạnh bên bằng cạnh đáy và bằng a. Gọi M là trung điểm của SC. Tính góc giữa hai mặt phẳng (MBD) và (ABCD).

    Tính góc giữa hai mặt phẳng (MBD) và(ABCD)

    Gọi O là tâm hình vuông ABCD, suy ra SO ⊥ (ABCD).

    Ta có: \left\{ {\begin{array}{*{20}{c}} {BD \bot SO} \\ {BD \bot AO} \end{array}} ight. \Rightarrow BD \bot \left( {SAC} ight) \Rightarrow BD \bot OM

    Do \left\{ {\begin{array}{*{20}{l}} {(MBD) \cap (ABCD) = BD} \\ {OM \subset (MBD)} \\ {OM \bot BD} \\ {OC \subset (ABCD)} \\ {OC \bot BD} \end{array}} ight.

    \Rightarrow \widehat {\left( {MBD),(ABCD)} ight)} = (\widehat {OM,OC}) = \widehat {MOC}

    Tam giác SOC vuông tại O, trung tuyến OM, suy ra OM = MC = \frac{{CS}}{2} = \frac{a}{2}

    => Tam giác MOC cân tại M.

    => OC = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}

    Khi đó \cos \widehat {MOC} = \frac{{OC}}{{SC}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{a} = \frac{{\sqrt 2 }}{2} \Rightarrow \widehat {MOC} = {45^{^0}}

    Vậy \widehat {\left( {\left( {MDB} ight);\left( {ABCD} ight)} ight)} = {45^0}

  • Câu 27: Thông hiểu

    Có bao nhiêu giá trị nguyên của tham số m trên đoạn \lbrack - 2018;2018brack để hàm số y = \ln\left( x^{2} - 2x - m + 1 ight) có tập xác định \mathbb{R}?

    Hàm số y = \ln\left( x^{2} - 2x - m + 1 ight) xác định trên \mathbb{R} khi và chỉ khi

    x^{2} - 2x - m + 1 > 0;\forall x \in \mathbb{R}

    \Leftrightarrow \left\{ \begin{matrix} a > 0 \\ \Delta' < 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} 1 > 0 \\ 1 + m - 1 < 0 \\ \end{matrix} ight.\ \Rightarrow m < 0

    Do \left\{ \begin{matrix} m\mathbb{\in Z} \\ m \in \lbrack - 2018;2018brack \\ \end{matrix} ight.

    \Rightarrow m \in \left\{ - 2018; - 2017;...; - 1 ight\}

    Vậy có 2018 giá trị của m thỏa mãn yêu cầu bài toán.

  • Câu 28: Nhận biết

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với mặt phẳng (ABCD). Tìm khẳng định đúng trong các khẳng định sau:

    Khẳng định đúng là “AB vuông góc với mặt phẳng (SAD)”

    Thật vậy, do SA ⊥ (ABCD) nên SA ⊥ AB

    Mặt khác AB ⊥ AD.

    Từ đó suy ra AB ⊥ (SDA)

  • Câu 29: Nhận biết

    Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, tam giác SAB cân. Giả sử E;F lần lượt là trung điểm các cạnh AB;CD. Khẳng định nào dưới đây sai?

    Hình vẽ minh họa

    Vì tam giác SAB là tam giác cân tại S nên SE\bot AB

    Ta có: \left\{ \begin{matrix} AB//CD \\ SE\bot AB \\ \end{matrix} ight.\ \Rightarrow SE\bot CD

  • Câu 30: Nhận biết

    Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OB = OC = a. Tính khoảng cách giữa hai đường thẳng OA và BC.

    Hình vẽ minh họa:

    Gọi M là trung điểm CB, ta có: OM ⊥ BC.

    Mặt khác vì OA, OB, OC đôi một vuông góc nên OA ⊥ (OBC)

    => OA ⊥ OM. Do đó khoảng cách giữa OA và BC là OM.

    Ta có: OM = \frac{1}{2}BC = \frac{a\sqrt{2}}{2}

  • Câu 31: Vận dụng

    Cho hàm số y = f(x) xác định bởi công thức y = f(x) = \ln\left( \frac{x}{x + 2} ight) . Tính giá trị biểu thức: S = f'(1) + f'(3) + f'(5) + ... + f'(2021) ?

    Kết quả: S = 2022/2023

    (Kết quả ghi dưới dạng phân số tối giản dạng a/b)

    Đáp án là:

    Cho hàm số y = f(x) xác định bởi công thức y = f(x) = \ln\left( \frac{x}{x + 2} ight) . Tính giá trị biểu thức: S = f'(1) + f'(3) + f'(5) + ... + f'(2021) ?

    Kết quả: S = 2022/2023

    (Kết quả ghi dưới dạng phân số tối giản dạng a/b)

    Ta có:

    y = f(x) = \ln\left( \frac{x}{x + 2} ight)

    \Rightarrow f'(x) = \frac{2}{x(x + 2)} = \frac{1}{x} - \frac{1}{x + 2}

    Khi đó:

    S = f'(1) + f'(3) + f'(5) + ... + f'(2021)

    S = \frac{1}{1} - \frac{1}{3} + \frac{1}{3} - \frac{1}{5} + ... + \frac{1}{2021} - \frac{1}{2023}

    S = 1 - \frac{1}{2023} = \frac{2022}{2023}

  • Câu 32: Vận dụng

    Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với AB = 2a, AD = DC = a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Góc giữa SC và mặt đáy bằng 600. Tính khoảng cách d giữa hai đường thẳng AC và SB.

    Hình vẽ minh họa:

    Xác định góc 600

    \widehat{\left( SC;(ABCD) ight)} =\widehat{(SC;AC)} = 60^{0} = \widehat{SCA}

    SA = AC.tan\widehat{SCA} =a\sqrt{6}

    Gọi M là trung điểm AB => ADCM là hình vuông => CM = AD = a

    Xét tam giác ACB ta có:

    CM = a = \frac{1}{2}AB

    => Tam giác ACB vuông tại C

    Lấy điểm E sao cho ACBE là hình chữ nhật

    => AC // BE

    => d(AC, SB) = d(AC, (SBE)) = d(A,(SBE))

    Kẻ AK ⊥ SE. Khi đó:

    d\left( A;(SBE) ight) = AK =\frac{SA.AE}{\sqrt{SA^{2} + AE^{2}}} = \frac{a\sqrt{6}}{2}

  • Câu 33: Vận dụng cao

    Lấy ngẫu nhiên 5 quả cầu từ hộp có 4 quả xanh, 5 quả đỏ và 6 quả vàng. Xác suất để lấy được 5 quả cầu có đủ 3 màu?

    Kết quả: 310/429

    (Kết quả ghi dưới dạng phân số tối giản a/b)

    Đáp án là:

    Lấy ngẫu nhiên 5 quả cầu từ hộp có 4 quả xanh, 5 quả đỏ và 6 quả vàng. Xác suất để lấy được 5 quả cầu có đủ 3 màu?

    Kết quả: 310/429

    (Kết quả ghi dưới dạng phân số tối giản a/b)

    Số phần tử không gian mẫu n(\Omega) =C_{15}^{5} = 3003

    Gọi A là biến cố lấy được 5 quả cầu đủ 3 màu

    => \overline{A} là biến cố 5 quả cầu lấy được không đủ 3 màu. Khi đó ta có các trường hợp như sau:

    TH1: lấy được 5 quả cầu đỏ có 1 cách

    TH2: lấy được 5 quả màu vàng có C_{6}^{5}= 6 cách

    TH3: lấy được chỉ có xanh và đỏ C_{4}^{4}.C_{5}^{1} + C_{4}^{3}.C_{5}^{2} +C_{4}^{2}.C_{5}^{3} + C_{4}^{1}.C_{5}^{4} = 125 cách

    TH4: lấy được chỉ có xanh và vàng C_{4}^{4}.C_{6}^{1} + C_{4}^{3}.C_{6}^{2} +C_{4}^{2}.C_{6}^{3} + C_{4}^{1}.C_{6}^{4} = 246 cách

    TH5: lấy được chỉ có đỏ và vàng C_{5}^{4}.C_{6}^{1} + C_{5}^{3}.C_{6}^{2} +C_{5}^{2}.C_{6}^{3} + C_{5}^{1}.C_{6}^{4} = 455 cách

    Vậy n\left( \overline{A} ight) = 833\Rightarrow n(A) = n(\Omega) - n\left( \overline{A} ight) =2170

    \Rightarrow P(A) =\frac{310}{429}

  • Câu 34: Nhận biết

    Cho ba đường thẳng phân biệt a, b, c. Mệnh đề nào sau đây đúng?

    Khi cho ba đường thẳng phân biệt a, b, c thì mệnh đề : “Nếu a song song với b và c vuông góc với a thì c vuông góc với b” là mệnh đề đúng.

  • Câu 35: Thông hiểu

    Gọi (C) là đồ thị hàm số y = - x^{3} + 3x^{2} - 3. Có bao nhiêu phương trình tiếp tuyến của (C) vuông góc với đường thẳng y = \frac{x}{9} + 2000?

    Gọi A\left( x_{0};y_{0} ight)là tiếp điểm của tiếp tuyến

    Ta có:

    y' = - 3x^{2} + 6x

    Vì tiếp tuyến của (C) vuông góc với đường thẳng y = \frac{x}{9} + 2000 nên y'\left( x_{0} ight).\frac{1}{9} = - 1 \Rightarrow y'\left( x_{0} ight) = - 9

    \Leftrightarrow - 3{x_{0}}^{2} + 6x_{0} + 9 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x_{0} = - 1 \\ x_{0} = 3 \\ \end{matrix} ight.

    Với x_{0} = - 1 \Rightarrow y_{0} = 1 nên phương trình tiếp tuyến tương ứng là

    y = - 9(x + 1) + 1 \Rightarrow y = - 9x - 8

    Với x_{0} = 3 \Rightarrow y_{0} = - 3 nên phương trình tiếp tuyến tương ứng là

    y = - 9(x - 3) - 3 \Rightarrow y = - 9x + 24

    Vậy có hai phương trình tiếp tuyến thỏa mãn điều kiện đề bài.

  • Câu 36: Thông hiểu

    Số cách chọn một tập hợp gồm 5 chữ cái từ bảng chữ cái Tiếng Anh là:

    Bảng chữ cái Tiếng Anh có 26 chữ cái.

    Suy ra số cách chọn 1 tập hợp gồm 5 chữ cái từ 26 chữ cái là: C_{26}^{5} = 65780 cách chọn.

  • Câu 37: Thông hiểu

    Phương trình \log_{2}(x - 1) = \log_{2}(2x + 1) có tập nghiệm là:

    Điều kiện \left\{ \begin{matrix}x - 1 > 0 \\2x + 1 > 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x > 1 \\x > - \dfrac{1}{2} \\\end{matrix} ight.\ \Leftrightarrow x > 1

    Ta có:

    \log_{2}(x - 1) = \log_{2}(2x +1)

    \Leftrightarrow x - 1 = 2x + 1 \Leftrightarrow x = - 2(ktm)

    Vậy phương trình vô nghiệm hay S = \varnothing.

  • Câu 38: Thông hiểu

    Có ba chiếc hộp đựng những tấm thẻ màu xanh và màu đỏ. Từ mỗi hộp lấy ngẫu nhiên 1 chiếc thẻ. Giả sử Q_{i} là biến cố lấy được tấm thẻ màu xanh từ hộp thứ i;i \in \left\{ 1;2;3 ight\}. Em hãy chọn đáp án đúng biểu diễn biến cố lấy được ít nhất một tấm thẻ màu đỏ dưới đây?

    Biểu diễn đúng là: \overline{Q_{1}} \cup \overline{Q_{2}} \cup \overline{Q_{3}}

  • Câu 39: Nhận biết

    Giá trị B = \sqrt[3]{2021}.\sqrt[5]{2021} viết dưới dạng lũy thừa với số mũ hữu tỉ là:

    Ta có:

    B = \sqrt[3]{2021}.\sqrt[5]{2021} = 2021^{\frac{1}{3}}.2021^{\frac{1}{5}} = 2021^{\frac{1}{3} + \frac{1}{5}} = 2021^{\frac{8}{15}}

  • Câu 40: Nhận biết

    Tìm mệnh đề đúng trong các mệnh đề sau:

    Đáp án đúng: “Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.”

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi HK2 Toán 11 Chân trời sáng tạo - Đề 4 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án Làm lại
  • 2 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi HK2 Toán 11 Chân trời sáng tạo - Đề 4
Thời gian còn lại 90:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập