Lớp 10 Toán 10 - Chân trời sáng tạo

Đề thi học kì 1 Toán 10 Chân trời sáng tạo Đề 3

Mô tả thêm: Đề thi học kì 1 Toán 10 được biên soạn giúp bạn học có thêm tài liệu ôn thi, củng cố nội dung kiến thức Toán 10 Chân trời sáng tạo.
  • Thời gian làm: 90 phút
  • Số câu hỏi: 45 câu
  • Số điểm tối đa: 45 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Thông hiểu

    Cho tam giác ABC, biết BC = 24, AC = 13, AB = 15. Số đo góc A là:

    Áp dụng hệ quả định lí cosin cho tam giác ABC ta có:

    \begin{matrix} \cos \widehat A = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} \hfill \\ \Rightarrow \cos \widehat A = \dfrac{{{{15}^2} + {{13}^2} - {{24}^2}}}{{2.15.13}} = - \dfrac{7}{{15}} \hfill \\ \Rightarrow \widehat A \approx {117^0}49\prime \hfill \\ \end{matrix}

  • Câu 2: Vận dụng

    Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây. Khẳng định nào sau đây là đúng?

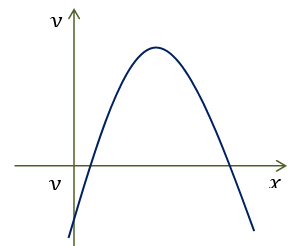
    Nhìn vào đồ thị ta có:

    Bề lõm hướng xuống  ⇒ a < 0.

    Hoành độ đỉnh x = - \frac{b}{2a} > 0\Rightarrow \frac{b}{2a} < 0 \Rightarrow b > 0 .

    Đồ thị hàm số cắt trục tung tại điểm có tung độ âm  ⇒ c < 0.

    Do đó: a < 0, b > 0, c < 0.

  • Câu 3: Nhận biết

    Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo ĐÚNG?

     Nếu a chia hết cho 3 thì a chia hết cho 9 có mệnh đề đảo là Nếu a chia hết cho 9 thì a chia hết cho 3. Đây là mệnh đề đảo đúng.

  • Câu 4: Thông hiểu

    Cho hai tập hợp A = ( - 3;5brack,B = \lbrack a; + \infty). Tìm a để A \cap B có đúng một phần tử.

    Để A \cap B có đúng một phần tử khi và chỉ khi a = 5. Khi đó A \cap B = \{ 5\}.

    Vậy a = 5 là giá trị cần tìm.

  • Câu 5: Vận dụng cao

    Cho biểu thức B xác định, rút gọn biểu thức

    B = \sqrt{2} - \frac{1}{\sin(x + 2013\pi)}.\sqrt{\frac{1}{1 + \cos x} + \frac{1}{1 - \cos x}} với \pi < x < 2\pi?

    Ta có:

    \sin(x + 2013\pi) = \sin(x + \pi + 2012\pi) = \sin(x + \pi) = - \sin x

    Do đó:

    B = \sqrt{2} - \frac{1}{\sin(x + 2013\pi)}.\sqrt{\frac{1}{1 + \cos x} + \frac{1}{1 - \cos x}}

    B = \sqrt{2} + \frac{1}{\sin x}.\sqrt{\frac{1 - \cos x + 1 + \cos x}{\left( 1 + \cos x ight)\left( 1 - \cos x ight)}}

    B = \sqrt{2} + \dfrac{1}{\sin x}.\sqrt{\dfrac{2}{1 - \cos^{2}x}}

    B = \sqrt{2} + \frac{1}{\sin x}.\sqrt{\dfrac{2}{\sin^{2}x}}

    B = \sqrt{2}\left( 1 + \frac{1}{\sin x.\left| \sin x ight|} ight)

    Vì \pi < x < 2\pi nên \sin x < 0

    \Rightarrow B = \sqrt{2}\left( 1 -\dfrac{1}{\sin^{2}x} ight) = - \sqrt{2}\cot^{2}x

  • Câu 6: Thông hiểu

    Tam giác đều ABC có đường cao AH. Khẳng định nào sau đây là đúng?

    Hình ảnh minh họa

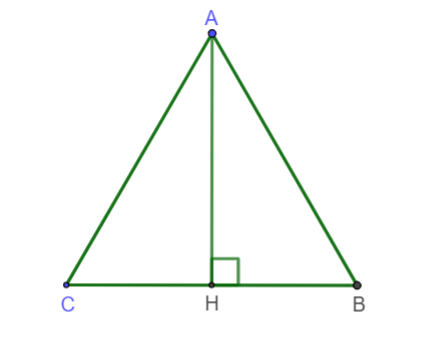
    Chọn khẳng định đúng

    Do tam giác ABC là tam giác đều có AH là đường cao nên đồng thời là đường phân giác

    => \widehat {BAH} = \frac{1}{2}\widehat {BAC}=30^0;\widehat {ABC} = {60^0};\widehat {AHC} = {90^0}

    Do đó: \sin \widehat {BAH} = \frac{1}{2};\sin \widehat {BAH} = \frac{{\sqrt 3 }}{2}

    Ta có: \widehat {ABC} = {60^0} \Rightarrow \sin \widehat {ABC} = \frac{{\sqrt 3 }}{2}

  • Câu 7: Thông hiểu

    Cho hệ bất phương trình \left\{ \begin{matrix}2x - 5y - 1 > 0 \\2x + y + 5 > 0 \\x + y + 1 < 0 \\\end{matrix} ight.. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?

    Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.

    Với O(0;0) \Rightarrow \left\{\begin{matrix}2.0 - 5.0 - 1 > 0 \\2.0 + 0 + 5 > 0 \\0 + 0 + 1 < 0 \\\end{matrix} ight.. Bất phương trình thứ nhất và thứ ba sai nên không thỏa mãn.

    Với M(1;0) \Rightarrow \left\{\begin{matrix}2.1 - 5.0 - 1 > 0 \\2.1 + 0 + 5 > 0 \\1 + 0 + 1 < 0 \\\end{matrix} ight.. Bất phương trình thứ ba sai nên không thỏa mãn.

    Với N(0; - 3) \Rightarrow \left\{\begin{matrix}2.0 - 5.( - 3) - 1 > 0 \\2.0 + ( - 2) + 5 > 0 \\0 + ( - 2) + 1 < 0 \\\end{matrix} ight.. Đúng.

  • Câu 8: Thông hiểu

    Cho tam giác ABC có I,\ D lần lượt là trung điểm AB,\ CI, điểm N thuộc cạnh BC sao cho BN = 2NC. Đẳng thức nào sau đây đúng?

    Gọi K là trung điểm BN.

    Xét \Delta CKI ta có

    \left\{ \begin{matrix} DN//IK \\ DN = \frac{1}{2}IK \\ \end{matrix} ight.\ \ \ \ \Rightarrow \ \ \overrightarrow{DN} = \frac{1}{2}\overrightarrow{IK} (1)

    Xét \Delta ABN ta có

    \left\{ \begin{matrix} AN//IK \\ AN = \frac{1}{2}IK \\ \end{matrix} ight.\ \ \ \ \Rightarrow \ \ \overrightarrow{AN} = 2\overrightarrow{IK} (2)

    Từ (1) và (2) suy ra \ \overrightarrow{AN} = 2\overrightarrow{IK} = 2.2\ \ \overrightarrow{DN} = 4\ \ \overrightarrow{DN}.

  • Câu 9: Vận dụng

    Phương trình (m−1)x2 − 2x + m + 1 = 0 có hai nghiệm phân biệt khi

    Yêu cầu bài toán \Leftrightarrow \left\{ \begin{matrix} a = m - 1 eq 0 \\ {\Delta'}_{x} = ( - \ 1)^{2} - (m - 1)(m + 1) > 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} m eq 1 \\ 1 - m^{2} + 1 > 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m eq 1 \\ m^{2} < 2 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} m eq 1 \\ - \ \sqrt{2} < m < \sqrt{2} \\ \end{matrix} ight.\ \Leftrightarrow m \in \left( - \ \sqrt{2};\sqrt{2} ight)\backslash\left\{ 1 ight\}.

    Vậy phương trình có hai nghiệm phân biệt \Leftrightarrow m \in \left( - \ \sqrt{2};\sqrt{2} ight)\backslash\left\{ 1 ight\}.

  • Câu 10: Nhận biết

    Gọi O là tâm hình vuông ABCD. Tính \overrightarrow{OB} - \overrightarrow{OC}.

    Ta có \overrightarrow{OB} - \overrightarrow{OC} = \overrightarrow{CB} = \overrightarrow{DA}.

  • Câu 11: Vận dụng

    Trong hệ tọa độ Oxy, cho hai điểm A(2; - 3),\ B(3;4). Tìm tọa độ điểm M thuộc trục hoành sao cho A,\ B,\ M thẳng hàng.

    Điểm M \in Ox\overset{}{ightarrow}M(m;0). Ta có \overrightarrow{AB} = (1;7) và \overrightarrow{AM} = (m - 2;3).

    ĐểA,B,M thẳng hàng \Leftrightarrow \overrightarrow{AB} cùng phương với \overrightarrow{AM} \Leftrightarrow \frac{m - 2}{1} = \frac{3}{7} \Leftrightarrow m = \frac{17}{7}.

  • Câu 12: Vận dụng

    Cho góc \widehat{xOy} = 30{^\circ}. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:

    Theo định lí hàm sin, ta có:

    \frac{OB}{\sin\widehat{OAB}} = \frac{AB}{\sin\widehat{AOB}} \Leftrightarrow OB = \frac{AB}{\sin\widehat{AOB}}.sin\widehat{OAB} = \frac{1}{sin30{^\circ}}.sin\widehat{OAB} = 2sin\widehat{OAB}

    Do đó, độ dài OB lớn nhất khi và chỉ khi \sin\widehat{OAB} = 1 \Leftrightarrow \widehat{OAB} = 90{^\circ}.

    Khi đó OB = 2.

  • Câu 13: Thông hiểu

    Cho hệ bất phương trình \left\{ \begin{matrix} x - 2y > 3 \\ - 3 + x - y < 0 \\ \end{matrix} ight. có tập nghiệm S. Khẳng định nào sau đây là khẳng định đúng ?

    Ta có: \left\{ \begin{matrix} x - 2y > 3 \\ - 2 + x - 2y < 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x > 2y + 3 \\ x < 2y + 2 \\ \end{matrix} ight.. Do đó không có điểm nào thỏa mãn hệ phương trình.

    Hệ này vô nghiệm.

  • Câu 14: Thông hiểu

    Cho \overrightarrow{OM} = ( - 2; - 1),\overrightarrow{ON} = (3; - 1). Tính góc của \left( \overrightarrow{OM},\overrightarrow{ON} ight).

    Ta có \cos\left(\overrightarrow{OM},\overrightarrow{ON} ight) =\frac{\overrightarrow{OM}.\overrightarrow{ON}}{\left|\overrightarrow{OM} ight|.\overrightarrow{|ON|}}= \frac{-5}{\sqrt{5}.\sqrt{10}} = - \frac{\sqrt{2}}{2} \Rightarrow \left(\overrightarrow{OM},\overrightarrow{ON} ight) = 135^{o}.

  • Câu 15: Vận dụng cao

    Các giá trị của tham số m để phương trình (2x - 1)^{2} + m = \sqrt{x^{2} - x + 1} (1) có nghiệm là:

    Đặt t = \sqrt{x^{2} - x + 1}

     ⇒ t2 = x2 − x + 1 ⇒ (2x−1)2 = 4x2 − 4x + 1 = 4t2 − 3

    Vì x^{2} - x + 1 = \left( x - \frac{1}{2} ight)^{2} + \frac{3}{4} \geq \frac{3}{4} nên t \geq \frac{\sqrt{3}}{2}

    Phương trình (1) trở thành 4t2 − 3 + m = t ⇔  − 4t2 + t + 3 = m.

    Xét hàm số y =  − 4t2 + t − 3 với t \geq \frac{\sqrt{3}}{2}

    Ta có - \frac{b}{2a} = \frac{1}{8} < \frac{\sqrt{3}}{2}

    Bảng biến thiên

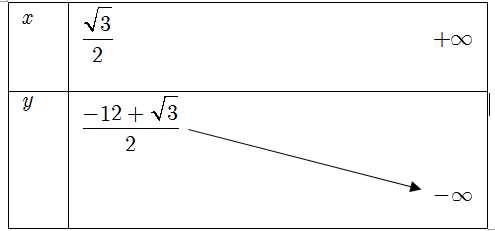
    Phương trình (1) có nghiệm ⇔ phương trình có nghiệm t \geq \frac{\sqrt{3}}{2}

    ⇔ đồ thị hàm số y =  − 4t2 + t − 3 trên \lbrack\frac{\sqrt{3}}{2}; + \infty) cắt đường thẳng y = m \Leftrightarrow m \leq \frac{- 12 + \sqrt{3}}{2} .

    Vậy phương trình (1) có nghiệm khi và chỉ khi m \leq \frac{- 12 + \sqrt{3}}{2}.

  • Câu 16: Nhận biết

    Điểm cuối của \alpha thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?

    Điểm cuối của \alpha thuộc góc phần tư thứ hai ightarrow \left\{ \begin{matrix} \sin\alpha < 0 \\ \cos\alpha < 0 \\ \tan\alpha > 0 \\ \cot\alpha > 0 \\ \end{matrix} ight..

  • Câu 17: Nhận biết

    Bất phương trình nào sau đây là bất phương trình bậc hai một ẩn?

    Bất phương trình bậc hai một ẩn là: 3x^{2} – 12x + 1 ≤ 0

  • Câu 18: Vận dụng

    Trong mặt phẳng tọa độ Oxy, gọi H(a,b) là trực tâm tam giác ABC có tọa độ các đỉnh A(3;1),B( - 1;2) và I(1; - 1) là trọng tâm tam giác ABC. Tính giá trị biểu thức K = a + 3b?

    Gọi C\left( x_{C};y_{C} ight). Vì I là trọng tâm tam giác ABC nên ta có hệ phương trình:

    \left\{ \begin{matrix}\dfrac{x_{A} + x_{B} + x_{C}}{2} = x_{I} \\\dfrac{y_{A} + y_{B} + y_{C}}{2} = y_{I} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x_{C} = 1 \\y_{C} = - 1 \\\end{matrix} ight.\ \Rightarrow C(1; - 4)

    Ta có: H(a,b) là trực tâm tam giác ABC nên \left\{ \begin{matrix} AH\bot BC \\ BH\bot AC \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} \overrightarrow{AH}.\overrightarrow{BC} = 0 \\ \overrightarrow{BH}.\overrightarrow{AC} = 0 \\ \end{matrix} ight.

    \left\{ \begin{matrix} \overrightarrow{AH} = (a - 3;b + 1);\overrightarrow{BC} = (2; - 6) \\ \overrightarrow{BH} = (a + 1;b - 2);\overrightarrow{AC} = ( - 2; - 3) \\ \end{matrix} ight.

    Ta có hệ phương trình \left\{\begin{matrix}2(a - 3) - 6(b + 1) = 0 \\- 2(a + 1) - 3(b - 2) = 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}a = \dfrac{10}{3} \\b = \dfrac{- 8}{9} \\\end{matrix} ight.

    Vậy biểu thức K = a + 3b = \frac{2}{3}

  • Câu 19: Nhận biết

    Trong mặt phẳng tọa độ Oxy, cho hai vectơ \overrightarrow{a} = ( - 2; - 1) và \overrightarrow{b} = (4; - 3). Tính cosin của góc giữa hai vectơ \overrightarrow{a} và \overrightarrow{b}.

    Ta có: \cos\left( \overrightarrow{a};\overrightarrow{b} ight) = \frac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a} ight|.\left| \overrightarrow{b} ight|} = \frac{- 5}{\sqrt{5}.5} = \frac{- \sqrt{5}}{5}.

  • Câu 20: Vận dụng cao

    Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là 27 và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.

    Gọi x đồng là số tiền mà doanh nghiệp A dự định giảm giá; (0≤x≤4).

    Khi đó:

    Lợi nhuận thu được khi bán một chiếc xe là 31 − x − 27 = 4 − x .

    Số xe mà doanh nghiệp sẽ bán được trong một năm là 600 + 200x .

    Lợi nhuận mà doanh nghiệp thu được trong một năm là

    f(x) = (4−x)(600+200x) =  − 200x2 + 200x + 2400.

    Xét hàm số f(x) =  − 200x2 + 200x + 2400 trên đoạn [0; 4] có bảng biến thiên

    Vậy \max_{\lbrack 0;4brack}f(x) = 2\ 450 \Leftrightarrow x = \frac{1}{2}.

    Vậy giá mới của chiếc xe là 30, 5 triệu đồng thì lợi nhuận thu được là cao nhất.

  • Câu 21: Vận dụng

    Trong các mệnh đề sau đây, mệnh đề nào có là đúng?

    + Nếu a + b chia hết cho c thì a và b cùng chia hết cho c \Rightarrow Mệnh đề sai. Ví dụ: 2 + 7 chia hết cho 3 nhưng 2 và 7 không chia hết cho 3.

    + Nếu 2 tam giác có diện tích bằng nhau thì bằng nhau \Rightarrow Mệnh đề sai. Ví dụ, 1 tam giác vuông và 1 tam giác đều có diện tích bằng nhau nhưng chúng không bằng nhau.

    + Nếu a chia hết cho 9 thì a chia hết cho 3 \Rightarrow Mệnh đề đúng.

    + Nếu một số chia hết cho 5 thì số đó tận cùng bằng 0 \Rightarrow Mệnh đề sai. Ví dụ 25 chia hết cho 5 nhưng không tận cùng bằng 0.

    Chọn đáp án: Nếu a chia hết cho 9 thì a chia hết cho 3.

  • Câu 22: Nhận biết

    Trên đường thẳng MN lấy điểm P sao cho \overrightarrow{MN} = - 3\overrightarrow{MP}. Điểm P được xác định đúng trong hình vẽ nào sau đây:

    Ta có \overrightarrow{MN} = - 3\overrightarrow{MP} nên MN = 3MP và \overrightarrow{MN} và \overrightarrow{MP} ngược hướng.

  • Câu 23: Thông hiểu

    Cho hình vuông ABCD. Khẳng định nào sau đây đúng?

    ABCD là hình vuông \Rightarrow \overrightarrow{AD} = \overrightarrow{BC} = - \overrightarrow{CB} \Rightarrow \left| \overrightarrow{AD} ight| = \left| \overrightarrow{CB} ight|.

  • Câu 24: Thông hiểu

    Tất cả các giá trị của tham số m để phương trình \frac{3mx + 1}{\sqrt{x + 1}} + \sqrt{x + 1} =\frac{2x + 5m + 3}{\sqrt{x + 1}} có nghiệm là:

    ĐKXĐ: x >  − 1

    pt ⇔ 3mx + 1 + x + 1 = 2x + 5m + 3 ⇔ (3m−1)x = 5m + 1.

    Phương trình đã cho có nghiệm \Leftrightarrow \left\{ \begin{matrix}3m - 1 eq 0 \\x = \frac{5m + 1}{3m - 1} > - 1 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}m eq \frac{1}{3} \\\frac{8m}{3m - 1} > 0 \\\end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix}m > \frac{1}{3} \\m < 0 \\\end{matrix} ight..

  • Câu 25: Thông hiểu

    Tính tổng tất cả các nghiệm của phương trình \sqrt{6 - 5x} = 2 - x?

    Ta có:

    \sqrt{6 - 5x} = 2 - x

    \Rightarrow \left\{ \begin{matrix} 2 - x \geq 0 \\ 6 - 5x = (2 - x)^{2} \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} x \leq 2 \\ x^{2} + x - 2 = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x \leq 2 \\ \left\lbrack \begin{matrix} x = 1 \\ x = - 2 \\ \end{matrix} ight.\ \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 2 \\ \end{matrix} ight.

    Vậy tổng các nghiệm của phương trình bằng 1 + ( - 2) = - 1.

  • Câu 26: Nhận biết

    Cho biết x là một phần tử của tập hợp A, xét các mệnh đề sau:

    (I) x \in A.

    (II) \left\{ x ight\} \in A.

    (III) x \subset A.

    (IV) \left\{ x ight\} \subset A.

    Trong các mệnh đề sau, mệnh đề nào là đúng:

    I đúng.

    II sai vì không có khái niệm tập hợp này thuộc tập hợp kia.

    III sai vì 1 phần tử thì không thể là con của 1 tập hợp.

    IV đúng.

  • Câu 27: Nhận biết

    Cho biết \tan\alpha = \frac{1}{2}. Tính \cot\alpha.

    Ta có: \tan\alpha.cot\alpha = 1 \Rightarrow \cot\alpha = \frac{1}{\tan\alpha} = \frac{1}{\frac{1}{2}} = 2.

  • Câu 28: Nhận biết

    Tam giác ABC có \widehat{B} = 60{^\circ},\ \ \widehat{C} = 45{^\circ} và AB = 5. Tính độ dài cạnh AC.

    Theo định lí hàm sin, ta có \frac{AB}{\sin\widehat{C}} = \frac{AC}{\sin\widehat{B}} \Leftrightarrow \frac{5}{sin45{^\circ}} = \frac{AC}{sin60{^\circ}} \Rightarrow AC = \frac{5\sqrt{6}}{2}.

  • Câu 29: Thông hiểu

    Tam giác ABC vuông ở A và có góc \widehat{B} = 50^{o}. Hệ thức nào sau đây là sai?

    Vì \left( \overrightarrow{AB},\ \overrightarrow{BC} ight) = 180^{0} - \left( \overrightarrow{AB},\ \overrightarrow{CB} ight) = 130^{o} nên loại \left( \overrightarrow{AB},\ \overrightarrow{BC} ight) = 130^{o}.

    Vì \left( \overrightarrow{BC},\ \overrightarrow{AC} ight) = \left( \overrightarrow{CB},\ \overrightarrow{CA} ight) = 40^{o} nên loại \left( \overrightarrow{BC},\ \overrightarrow{AC} ight) = 40^{o}.

    Vì \left( \overrightarrow{AB},\ \overrightarrow{CB} ight) = \left( \overrightarrow{BA},\ \overrightarrow{BC} ight) = 50^{o} nên loại \left( \overrightarrow{AB},\ \overrightarrow{CB} ight) = 50^{o}.

    Vì \left( \overrightarrow{AC},\ \overrightarrow{CB} ight) = 180^{0} - \left( \overrightarrow{CA},\ \overrightarrow{CB} ight) = 140^{o}nên chọn \left( \overrightarrow{AC},\ \overrightarrow{CB} ight) = 120^{o}.

  • Câu 30: Thông hiểu

    Cho hàm số y = \frac{x + 1}{x - 1}. Tìm tọa độ điểm thuộc đồ thị của hàm số và có tung độ bằng − 2.

    Gọi M0(x0;−2) là điểm thuộc đồ thị hàm số có tung độ bằng  − 2.

    Khi đó: \frac{x_{0} + 1}{x_{0} - 1} = - 2 \Leftrightarrow x_{0} + 1 = 2\left( 1 - x_{0} ight) \Leftrightarrow 3x_{0} = 1 \Leftrightarrow x_{0} = \frac{1}{3} \Rightarrow M\left( \frac{1}{3}; - 2 ight).

  • Câu 31: Vận dụng

    Cho tam giác ABC đều cạnh a. Gọi M là trung điểm BC. Khẳng định nào sau đây đúng?

    Tam giác ABC đều cạnh a nên độ dài đường trung tuyến bằng \frac{a\sqrt{3}}{2}.

    Chọn \left| \overrightarrow{AM} ight| = \frac{a\sqrt{3}}{2}.

  • Câu 32: Thông hiểu

    Tìm m để f(x) = x2 − 2(2m−3)x + 4m − 3 > 0,    ∀x ∈ ℝ?

    f(x) = x2 − 2(2m−3)x + 4m − 3 > 0, ∀x ∈ ℝ⇔Δ < 0 ⇔ 4m2 − 16m + 12 < 0 ⇔ 1 < m < 3.

  • Câu 33: Nhận biết

    Cho định lí “Nếu a < b thì a + c < b + c”. Giả thiết của định lí này là gì?

    Khi mệnh đề P ⇒ Q là định lí, ta nói: P là giả thiết, Q là kết luận của định lí

    Từ đó ta suy ra: Giả thiết của định lí là a < b

  • Câu 34: Nhận biết

    Vectơ có điểm đầu là D, điểm cuối là E được kí hiệu là

    Vectơ có điểm đầu là D, điểm cuối là E được kí hiệu là \overrightarrow{DE}.

  • Câu 35: Thông hiểu

    Trong mặt phẳng tọa độ Oxy, cho hai vecto \overrightarrow{a} = (5;m - 7) và \overrightarrow{b} = (m + 1;3) với m\mathbb{\in R}. Tìm giá trị của tham số m để \overrightarrow{a}\bot\overrightarrow{b}?

    Ta có:

    \overrightarrow{a}\bot\overrightarrow{b} \Leftrightarrow \overrightarrow{a}.\overrightarrow{b} = \overrightarrow{0}

    \Leftrightarrow 5(m - 1) + 3.(m - 7) = 0 \Leftrightarrow m = 2

    Vậy m = 2 thì hai vecto đã cho vuông góc với nhau.

  • Câu 36: Thông hiểu

    Cho mệnh đề chứa biến P(n):``n^{2} - 1 chia hết cho 4” với n là số nguyên. Xét xem các mệnh đề P(5) và P(2) đúng hay sai?

    Thay n = 5 và n = 2 vào P(n) ta được các số 24 \vdots 4 và 3 không chia hết cho 4. Vậy P(5) đúng và P(2) sai.

  • Câu 37: Nhận biết

    Cho bất phương trình 2x + 3y - 1 \leqslant 0 (1). Chọn khẳng định đúng trong các khẳng định sau:

    Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.

  • Câu 38: Nhận biết

    Cho hàm số y =  − x2 + 4x + 1. Khẳng định nào sau đây sai?

    Hàm số y = ax2 + bx + c với a < 0 nghịch biến trên khoảng \left( - \frac{b}{2a}; + \infty ight), đồng biến trên khoảng \left( - \infty; - \frac{b}{2a} ight).

    Áp dụng: Ta có - \frac{b}{2a} = 2. Do đó hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (−∞;2). Do đó Hàm số nghịch biến trên khoảng (4;+∞) và đồng biến trên khoảng (−∞;4) sai. Chọn đáp án này.

    Đáp án Trên khoảng (−∞;−1) hàm số đồng biến đúng vì hàm số đồng biến trên khoảng (−∞;2) thì đồng biến trên khoảng con (−∞;−1).

    Đáp án Trên khoảng (3;+∞) hàm số nghịch biến đúng vì hàm số nghịch biến trên khoảng (2;+∞) thì nghịch biến trên khoảng con (3;+∞).

  • Câu 39: Vận dụng cao

    Cho tập hợp A = (0; + \infty) và B = \left\{x\in\mathbb{ R}|mx^{2} - 4x + m - 3 = 0 ight\}, với m là tham số. Tìm m để B có đúng hai tập con và B \subset A?

    B có đúng hai tập con và B \subset A khi và chỉ khi phương trình mx^{2} - 4x + m - 3 = 0 (1) có đúng một nghiệm dương.

    Trường hợp 1. m = 0, phương trình (1) trở thành - 4x - 3 = 0 \Leftrightarrow x = - \frac{3}{4}

    Do đó m = 0 không thỏa đề bài.

    Trường hợp 2. m eq 0, khi đó phương trình (1) có đúng một nghiệm dương khi và chỉ khi

    \left\{ \begin{matrix}\Delta' = 0 \\S > 0 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}4 - m(m - 3) = 0 \\\dfrac{4}{m} > 0 \\\end{matrix} ight.

    \Leftrightarrow m = 4

    Vậy m = 4 là giá trị duy nhất thỏa mãn yêu cầu đề bài.

  • Câu 40: Nhận biết

    Cho hai điểm A và B phân biệt. Điều kiện để I là trung điểm AB là:

    Điều kiện để I là trung điểm AB là: \overrightarrow{IA} = - \overrightarrow{IB}.

  • Câu 41: Thông hiểu

    Cho tam giác ABC và điểm M thỏa mãn \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}. Xác định vị trí điểm M.

     Điểm M là trọng tâm tam giác ABC khi và chỉ khi \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}.

  • Câu 42: Thông hiểu

    Có bao nhiêu giá trị nguyên của tham số m sao cho hàm số x^{2} + (m - 1)x + m - 2 = 0 có hai nghiệm phân biệt thuộc khoảng ( - 5;5)?

    Ta có:

    PT \Leftrightarrow (x + 1)(x + m - 2) = 0

    \Leftrightarrow \left\lbrack \begin{matrix} x = - 1 \\ x = - m + 2 \\ \end{matrix} ight.

    Từ yêu cầu bài toán \Leftrightarrow \left\{ \begin{matrix} - m + 2 eq - 1 \\ - 5 < - m + 2 < 5 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m eq 3 \\ - 3 < m < 7 \\ \end{matrix} ight.

    Suy ra m \in \left\{ - 2; - 1;0;1;2;4;5;6 ight\}

    Vậy có 8 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.

  • Câu 43: Thông hiểu

    Cho tam giác ABC có AB=\sqrt{3}+1, AC=\sqrt{6}, BC = 2. Số đo của \widehat{B}-\widehat{A} là:

    Áp dụng hệ quả của định lí cosin ta có:

    \begin{matrix} \cos \widehat A = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} \hfill \\ \Rightarrow \cos \widehat A = \dfrac{{{{\left( {\sqrt 3 + 1} ight)}^2} + {{\left( {\sqrt 6 } ight)}^2} - {2^2}}}{{2.\left( {\sqrt 3 + 1} ight).\sqrt 6 }} = \dfrac{{\sqrt 2 }}{2} \hfill \\ \Rightarrow \widehat A = {45^0} \hfill \\ \end{matrix}

    \begin{matrix} \cos \widehat B = \dfrac{{A{B^2} + B{C^2} - A{C^2}}}{{2AB.BC}} \hfill \\ \Rightarrow \cos \widehat B = \dfrac{{{{\left( {\sqrt 3 + 1} ight)}^2} + {2^2} - {{\left( {\sqrt 6 } ight)}^2}}}{{2.\left( {\sqrt 3 + 1} ight).2}} = \dfrac{1}{2} \hfill \\ \Rightarrow \widehat B = {60^0} \hfill \\ \Rightarrow \widehat B - \widehat A = {60^0} - {45^0} = {25^0} \hfill \\ \end{matrix}

  • Câu 44: Nhận biết

    Trong mặt phẳng tọa độ Oxy, tọa độ vecto \overrightarrow{w} = 8\overrightarrow{j} - 3\overrightarrow{i} là:

    Ta có: \left\{ \begin{matrix} \overrightarrow{i} = (1;0) \\ \overrightarrow{j} = (0;1) \\ \end{matrix} ight.\ \Rightarrow \overrightarrow{w} = 8\overrightarrow{j} - 3\overrightarrow{i} = ( - 3;8).

  • Câu 45: Thông hiểu

    Cặp số nào sau đây là nghiệm của bất phương trình 3x - 5y > 12?

    Xét đáp án (0; 3) ta có: x = 0; y = 3 thay vào bất phương trình ta được:

    3.0 - 5.3 = - 15 < 12

    Vậy (0;3) không là cặp nghiệm của bất phương trình

    Xét đáp án (6; 1) ta có: x = 6; y = 1 thay vào bất phương trình ta được:

    3.6- 5.1=13> 12

    Vậy (6; 1) là cặp nghiệm của bất phương trình.

    Xét đáp án (2; 4) ta có: x = 2; y = 4 thay vào bất phương trình ta được:

    3.2 - 5.4 = - 14 < 12

    Vậy (2; 4) không là cặp nghiệm của bất phương trình.

    Xét đáp án (3; 2) ta có: x = 3; y = 2 thay vào bất phương trình ta được:

    3.3 - 5.2 = - 1 < 12

    Vậy (3; 2) không là cặp nghiệm của bất phương trình.

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 10 Chân trời sáng tạo Đề 3 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án
Làm lại
  • 4 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi học kì 1 Toán 10 Chân trời sáng tạo Đề 3
Thời gian còn lại 90:00 Số câu đã làm 0/45
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập