Lớp 11 Toán 11 - Cánh Diều

Đề thi học kì 1 Toán 11 Cánh Diều Đề 1

Mời các bạn học cùng thử sức với Đề thi học kì 1 Toán 11 Cánh Diều nha!

  • Thời gian làm: 90 phút
  • Số câu hỏi: 44 câu
  • Số điểm tối đa: 44 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Nhận biết

    Điều kiện xác định của hàm số y = f\left( x ight) = \frac{{2\cos x - 1}}{{\sin x}}

     Điều kiện xác định của hàm số:

    \begin{matrix} \sin x e 0 \hfill \\ \Leftrightarrow x e k\pi ,k \in \mathbb{Z} \hfill \\ \end{matrix}

  • Câu 2: Thông hiểu

    Cho hình chóp tứ giác S.ABCD, I = AC \cap BD. Giả sử mặt phẳng (\alpha) bất kì cắt các cạnh SA,SB,SC,SD lần lượt tại A',B',C',D'. Chọn khẳng định đúng trong các khẳng định sau.

    Hình vẽ minh hoạ

    Ta thấy: \left\{ \begin{matrix} A'C' = (\alpha) \cap (SAC) \\ B'D' = (\alpha) \cap (SBD) \\ SI = (SBD) \cap (SAC) \\ \end{matrix} ight.

    => Các đường thẳng A'C',B'D',SI đồng quy.

  • Câu 3: Thông hiểu

    Phương trình  \cos\frac{\pi}{3} = \cos x có nghiệm là:

    Ta có:

    \cos\frac{\pi}{3} = \cos x

    \Leftrightarrow x = \pm \frac{\pi}{3} +k2\pi;\left( k\mathbb{\in Z} ight)

  • Câu 4: Vận dụng

    Cho hàm số y =f(x) = \cos2x - 4\cos x + 4. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x)?

    Ta có:

    y =f(x) = \cos2x - 4\cos x + 4

    = 2\cos^{2}x - 4\cos x + 3

    Đặt \cos x = t,t \in \lbrack - 1;1brack. Xét hàm số f(t) = 2t^{2} - 4t + 3 trên đoạn \lbrack - 1;1brack

    Ta có bảng biến thiên

    Từ bảng biến thiên ta có: \left\{ \begin{matrix} \max y = \max\underset{t \in \lbrack - 1;1brack}{f(t)} = 9 \\ \min y = \min\underset{t \in \lbrack - 1;1brack}{f(t)} = 1 \\ \end{matrix} ight.

    Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho là 10.

  • Câu 5: Thông hiểu

    Tìm giới hạn H = \lim_{x ightarrow 1}\left( \frac{3x^{2} - x - 2}{x^{2} - 1} ight)

    Ta có:

    H = \lim_{x ightarrow 1}\left( \frac{3x^{2} - x - 2}{x^{2} - 1} ight)

    H = \lim_{x ightarrow 1}\frac{(x - 1)(3x + 2)}{(x - 1)(x + 1)}

    H = \lim_{x ightarrow 1}\frac{3x + 2}{x + 1} = \frac{5}{2}

  • Câu 6: Vận dụng cao

    Có bao nhiêu giá trị nguyên của m để phương trình 3sinx + m - 1 = 0 có nghiệm?

    Ta có:

    \begin{matrix} \sin x = \dfrac{{1 - m}}{3} \in \left[ { - 1;1} ight] \hfill \\ \Rightarrow - 3 \leqslant - m \leqslant \Leftrightarrow - 2 \leqslant m \leqslant 4 \hfill \\ \end{matrix}

    Kết hợp với m thuộc tập số nguyên

    Suy ra 4 – (-2) + 1 = 7 giá trị nguyên của m

  • Câu 7: Vận dụng

    Cho hình lăng trụ ABC.A’B’C’. Gọi I. J. K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’. Mặt phẳng nào sau đây song song với (IJK)

    Hình vẽ minh họa

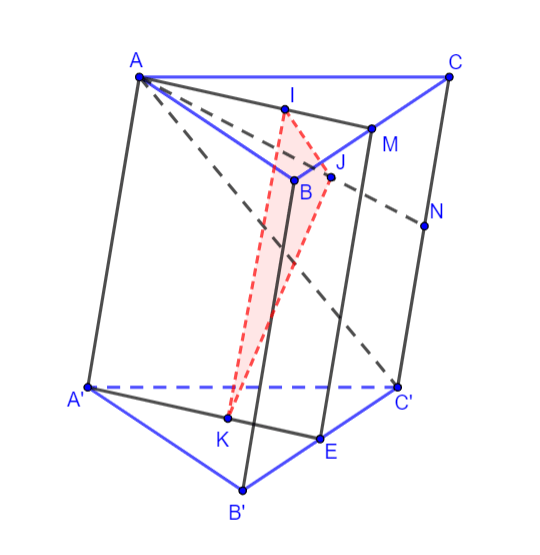
    Mặt phẳng nào song song với (IJK)

    Gọi M, N, E lần lượt là trung điểm của BC, CC' và B'C'.

    => \frac{{AI}}{{IM}} = \frac{{AJ}}{{JN}} = 2 (tính chất trọng tâm tam giác)

    => IJ//MN(1)

    Xét mặt phẳng (AA'EM) ta có: \frac{{AI}}{{IM}} = \frac{{A'K}}{{KE}} = 2

    => IK//ME

    Mà ME //BB'

    => IK//BB'(2)

    Từ (1) và (2) => (IJK) và (BB'C)là hai mặt phẳng phân biệt. Khi đó ta có:

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {\left( {IJK} ight) e \left( {BB'C'} ight)} \\ {IJ,IK \subset \left( {IJK} ight)} \\ {MN,BB' \subset \left( {BB'C'} ight)} \end{array}} ight. \hfill \\ \Rightarrow \left( {IJK} ight)//\left( {BB'C'} ight) \hfill \\ \end{matrix}

  • Câu 8: Nhận biết

    Trong các phát biểu sau, phát biểu nào là sai?

    Ta lấy một phản ví dụ:

    Dãy số (un) với {u_n} = n - 2 là cấp số cộng có công sai d = 1 > 0

    Nhưng dạng khai triển của nó là -1; 0; 1; … không phải một dãy số dương.

  • Câu 9: Thông hiểu

    Cho hình chóp S \cdot ABCD có đáy ABCD là hình bình hành. Gọi là giao điểm của hai đường chéo hình bình hành. Một mặt phẳng (\alpha) qua O, song song với SA,CD. Thiết diện tạo bởi (\alpha) và hình chóp là hình gì?

    Hình vẽ minh họa

    Do (a) // CD nên giao tuyến d = (a) ∩ (ABCD) là đường thẳng qua O và song song với CD. Gọi G, H lần lượt là giao điểm của d với BC,AD.

    Do (a) // SA nên giao tuyến a = (a) ∩ (SAB) là đường thẳng qua H và song song với SA.

    Gọi I là giao điểm của a với SD.

    Do (a) // CD nên giao tuyến b = (a) ∩ (SCD) là đường thẳng qua I và song song với CD.

    Gọi J lần lượt là giao điểm của b với SC.

    Vậy thiết diện tạo bởi (a) và hình chóp là hình thang GHIJ vì GH // IJ //CD.

  • Câu 10: Vận dụng

    Cho tứ diện ABCD. Các cạnh AC,BD,AB,CD,AD,BC có trung điểm lần lượt là M,N,P,Q,R,S. Bốn điểm nào sau đây không cùng thuộc một mặt phẳng?

    Hình vẽ minh họa

    Ta có:

    MP // BC // NQ, MP = \frac{1}{2}BC = NQ

    => MPNQ là hình bình hành

    => M, N, P, Q thuộc một mặt phẳng.

    MR // CD // SN, MR = \frac{1}{2}CD = SN

    => MRNS là hình bình hành

    => M, R, S, N thuộc một mặt phẳng.

    PS // AC // RQ, PS = \frac{1}{2}AC = RQ

    => PSQR là hình bình hành nên P, Q, R, S thuộc một mặt phẳng.

    Vậy M,P,R,S không thuộc cùng một mặt phẳng.

  • Câu 11: Nhận biết

    Giá trị của \lim\frac{\sqrt{n + 1}}{n + 2} bằng:

    Với mọi số thực a>0 nhỏ tùy ý, ta chọn n_{a} = \left\lbrack \frac{1}{a^{2}} - 1 ightbrack + 1

    Ta có:

    \frac{\sqrt{n + 1}}{n + 2} < \frac{1}{\sqrt{n + 1}} < a  với mọi n > n_{a}

    Suy ra \lim\frac{\sqrt{n + 1}}{n + 2} = 0

  • Câu 12: Nhận biết

    Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình \sqrt 3 \cos x + m - 1 = 0 có nghiệm?

     Ta có \sqrt 3 \cos x + m - 1 = 0 \Leftrightarrow \cos x = \frac{{1 - m}}{{\sqrt 3 }}.

    Phương trình có nghiệm \Leftrightarrow - 1 \leqslant \frac{{1 - m}}{{\sqrt 3 }} \leqslant 1

    \Leftrightarrow 1 - \sqrt 3 \leqslant m \leqslant 1 + \sqrt 3 \xrightarrow{{m \in \mathbb{Z}}}m \in \left\{ {0;1;2} ight\}

    Vậy có tất cả 3 giá trị nguyên của tham số m.

  • Câu 13: Thông hiểu

    Cho cấp số cộng \left( u_{n} ight) có u_{1} = - 1;d = 3. Số 100 là số hạng thứ mấy của cấp số cộng?

    Ta có: \left\{ \begin{matrix} u_{1} = - 1 \\ d = 3 \\ \end{matrix} ight.

    \overset{n \mapsto u_{n} = 100}{ightarrow}100 = u_{1} + (n - 1)d

    \Leftrightarrow 100 = 3n - 8

    \Leftrightarrow n = 36

  • Câu 14: Vận dụng cao

    Một quả bóng cao su được thả từ độ cao 81m. Mỗi lần chạm đất quả bóng lại nảy lên hai phần ba độ cao của lần rơi trước. Tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho đến lúc bóng không nảy nữa bằng

    Đáp án 405

    Đáp án là:

    Một quả bóng cao su được thả từ độ cao 81m. Mỗi lần chạm đất quả bóng lại nảy lên hai phần ba độ cao của lần rơi trước. Tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho đến lúc bóng không nảy nữa bằng

    Đáp án 405

    Gọi r_{i} là khoảng cách lần rơi thứ i

    Ta có r_{1} = 81, r_{2} = \frac{2}{3}.81,…, r_{n} = \left( \frac{2}{3} ight)^{n - 1}.81,…

    Suy ra tổng các khoảng cách rơi của quả bóng từ lúc thả bóng cho đến lần rơi thứ n bằng 81.\frac{1 - \left( \frac{2}{3} ight)^{n}}{1 - \frac{2}{3}}.

    Gọi t_{i} là khoảng cách lần nảy thứ i

    Ta có t_{1} = \frac{2}{3}.81, t_{2} = \left( \frac{2}{3} ight).\frac{2}{3}81,…, t_{n} = \left( \frac{2}{3} ight)^{n - 1}\frac{2}{3}.81,…

    Suy ra tổng các khoảng cách nảy của quả bóng từ lúc thả bóng cho đến đến lần nảy thứ n bằng \dfrac{2}{3}.81.\dfrac{1 - \left( \dfrac{2}{3}ight)^{n - 1}}{1 - \dfrac{2}{3}}.

    Vậy tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho đến lúc bóng không nảy nữa bằng S = \lim\left( 81.\frac{1 - \left( \frac{2}{3} ight)^{n}}{1 - \frac{2}{3}} + \frac{2}{3}.81.\frac{1 - \left( \frac{2}{3} ight)^{n - 1}}{1 - \frac{2}{3}} ight) = 405.

  • Câu 15: Vận dụng cao

    Cho hàm số y = x \sin x, số nghiệm thuộc \left[ { - \frac{\pi }{2};2\pi } ight] của phương trình y''+y=1 là?

     Ta có: y' = \operatorname{s} {\text{inx}} + x\cos x

    y'' = \cos x + \cos x - x\sin x = 2\cos x - x\sin x

    Do đó

    y'' + y = 1 \Leftrightarrow 2\cos x = 1 \Leftrightarrow \cos x = \frac{1}{2}

    \Leftrightarrow \left[ \begin{gathered} x = \frac{\pi }{3} + k2\pi \hfill \\ x = - \frac{\pi }{3} + k2\pi \hfill \\ \end{gathered} ight.\,\,\left( {k \in Z} ight)

    +) Trường hợp 1. Với x = \frac{\pi }{3} + k2\pi \,\,\left( {k \in Z} ight)

    Do x \in \left[ { - \frac{\pi }{2};2\pi } ight] nên - \frac{\pi }{2} \leqslant \frac{\pi }{3} + k2\pi \leqslant 2\pi \Leftrightarrow - \frac{5}{{12}} \leqslant k \leqslant \frac{5}{6}

    Suy ra k = 0 ta được x = \frac{\pi }{3}.

    +) Trường hợp 2. Với x = -\frac{\pi }{3} + k2\pi \,\,\left( {k \in Z} ight)

    Do x \in \left[ { - \frac{\pi }{2};2\pi } ight] nên - \frac{\pi }{2} \leqslant -\frac{\pi }{3} + k2\pi \leqslant 2\pi \Leftrightarrow - \frac{1}{{12}} \leqslant k \leqslant \frac{7}{6}

    Suy ra k = 0 ta được x = - \frac{\pi }{3};\,\,\,\,k = 1 ta được x = \frac{{5\pi }}{3}.

    Vậy có 3 nghiệm thuộc x \in \left[ { - \frac{\pi }{2};2\pi } ight] của phương trình y''+y=1 là

    x = \frac{\pi }{3}; x = -\frac{\pi }{3}; x = \frac{{5\pi }}{3}.

  • Câu 16: Nhận biết

    Tính giới hạn \lim_{x ightarrow 1}\frac{x^{2} + 3x - 4}{x - 1}

    Ta có:

    \lim_{x ightarrow 1}\frac{x^{2} + 3x - 4}{x - 1} = \lim_{x ightarrow 1}\frac{(x - 1)(x + 4)}{x - 1}

    = \lim_{x ightarrow 1}(x + 4) = 5

  • Câu 17: Thông hiểu

    Nếu \cos(a + b) = 0 thì khẳng định nào sau đây đúng?

    Ta có:

    \cos(a + b) = 0

    \Leftrightarrow a + b = \frac{\pi}{2} + k\pi

    \Leftrightarrow a = - b + \frac{\pi}{2} + k\pi

    \Rightarrow \left| \sin(a + 2b) ight| = \left| \sin\left( - b + 2b + \frac{\pi}{2} + k\pi ight) ight| = \left| \cos(b + k\pi) ight| = \left| \cos b ight|

  • Câu 18: Vận dụng

    Tính giới hạn \lim_{x ightarrow 2}\frac{\sqrt{x - 1} + x^{4} - 3x^{3} + x^{2} + 3}{\sqrt{2x} - 2}

    Ta có:

    \frac{\sqrt{x - 1} + x^{4} - 3x^{3} + x^{2} + 3}{\sqrt{2x} - 2}

    = \frac{\sqrt{x - 1} - 1}{\sqrt{2x} - 2} + \frac{x^{4} - 3x^{3} + x^{2} + 4}{\sqrt{2x} - 2}

    = \frac{(x - 2)\left( \sqrt{2x} + 2 ight)}{(2x - 4)\left( \sqrt{x - 1} + 1 ight)} + \frac{(x - 2)\left( x^{3} - x^{2} - x - 2 ight)\left( \sqrt{2x} + 2 ight)}{2x - 4}

    = \frac{\sqrt{2x} + 2}{2\left( \sqrt{x - 1} + 2 ight)} + \frac{\left( x^{3} - x^{2} - x - 2 ight)\left( \sqrt{2x} + 2 ight)}{2}

    Do đó \lim_{x ightarrow 2}\frac{\sqrt{x - 1} + x^{4} - 3x^{3} + x^{2} + 3}{\sqrt{2x} - 2} = 1

  • Câu 19: Nhận biết

    Cho phương trình 2x^{4} - 5x^{2} + x + 1 = 0. Chọn khẳng định đúng trong các khẳng định sau.

    Ta có: \left\{ \begin{matrix} f(0) = 1 \\ f(1) = - 1 \\ f(2) = 15 \\ \end{matrix} ight.

    => Phương trình có ít nhất hai nghiệm trên khoảng (0;2).

  • Câu 20: Nhận biết

    Cho hình chóp S.MNPQ. Có bao nhiêu cạnh của hình chóp chéo nhau với cạnh MN?

    Hình vẽ minh họa

    Các cạnh của hình chóp chéo nhau với cạnh MN là SP;SQ.

  • Câu 21: Thông hiểu

    Giải phương trình \sin\left( \frac{2x}{3} - \frac{\pi}{3} ight) = 0.

    Phương trình

    \sin\left( \frac{2x}{3} - \frac{\pi}{3} ight) = 0 \Leftrightarrow \frac{2x}{3} - \frac{\pi}{3} = k\pi

    \Leftrightarrow \frac{2x}{3} = \frac{\pi}{3} + k\pi \Leftrightarrow x = \frac{\pi}{2} + \frac{k3\pi}{2}\ \left( k\mathbb{\in Z} ight).

    Vậy đáp án cần tìm là: x = \frac{\pi}{2} + \frac{k3\pi}{2}\ \left( k\mathbb{\in Z} ight).

  • Câu 22: Nhận biết

    \lim(5n-4n^{3}) bằng

    Ta có: 

    \begin{matrix} \lim \left( {5n - 4{n^3}} ight) \hfill \\ = \lim \left[ {{n^3}\left( {\dfrac{5}{{{n^2}}} - 4} ight)} ight] \hfill \\ = - \infty \hfill \\ \end{matrix}

  • Câu 23: Nhận biết

    Khẳng định nào sai trong các khẳng định sau?

    Ta có:

    \cos6a = \cos^{2}3a -\sin^{2}3a

    = 2\cos^{2}3a - 1 = 1 -2\sin^{2}3a

  • Câu 24: Nhận biết

    Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?

    Hình vẽ minh họa

    Với 4 điểm không đồng phẳng A,B,C,D có thể xác định được 4 mặt phẳng phân biệt từ các điểm đó là (ABC),(BCD),(ACD),(ABD).

  • Câu 25: Thông hiểu

    Cho hình chóp S.ABC, tam giác ABC vuông tại A, \widehat{B} = 60^{0},AB = SB = a. Gọi I là trung điểm của BC, SB ⊥ AI. Giả sử mặt phẳng (P) là mặt phẳng đi qua M và song song với SB, AI. Xác định hình tạo bởi các giao tuyến của mặt phẳng (P) với các mặt của hình chóp.

    Hình vẽ minh họa

    Ta có: \left\{ \begin{matrix} (P) \cap (ABC) = M \\ (P)//AI \\ AI \subset (ABC) \\ \end{matrix} ight.

    Do đó giao tuyến của (P) với (ABC) là đường thẳng đi qua M và song song với AI cắt BC tại N.

    Tương tự \left\{ \begin{matrix} (\alpha) \cap (SAB) = MQ//SB;(M \in SA) \\ (\alpha) \cap (SBC) = NP//SB;(P \in SC) \\ \end{matrix} ight.

    Vậy giao tuyến của (P) với hình chóp S.ABC là tứ giác MNPQ.

  • Câu 26: Vận dụng cao

    Số thập phân vô hạn tuần hoàn 0,5111… được biểu diễn bởi phân số tối giản \frac{m}{n}. Tính tổng T = m + n.

    Ta có:

    0,5111... = 0,5 + 10^{- 2} + 10^{- 3} + ... + 10^{- n} + ...

    Dãy số 10^{- 2};10^{- 3};...;10^{- n};,,, là một cấp số nhân lùi vô hạn có số hạng đầu là u_{1} = 10^{- 2}, công sai là q = 10^{- 1}

    => S = \frac{u_{1}}{1 - q} = \frac{10^{- 2}}{1 - 10^{- 1}} = \frac{1}{90}

    Vậy 0,5111... = 0,5 + S = \frac{46}{90} = \frac{23}{45}

    \Rightarrow \left\{ \begin{matrix} m = 23 \\ n = 45 \\ \end{matrix} ight.\ \Rightarrow T = 68

  • Câu 27: Thông hiểu

    Kiểm tra sự đúng sai của các kết luận sau?

    a) Có hai trong ba hàm số y = \sin;y =\cos\sqrt{x};y = \tan x liên tục trên tập số thực. Sai||Đúng

    b) \lim_{x ightarrow - \infty}\left( \sqrt{x^{2} + 1} + x - 1 ight) = - 1 Đúng||Sai

    c) Phương trình 2x^{4} - 5x^{2} + x + 1 = 0 có ít nhất hai nghiệm thuộc khoảng (0;2).Đúng||Sai

    d) Biết hàm số f\left( x ight) = \left\{ \begin{gathered} \dfrac{{{x^2} + 1}}{{1 - x}}{\text{ khi x < 1}} \hfill \\ \sqrt {2x - 2} {\text{ khi x}} \geqslant {\text{1}} \hfill \\ \end{gathered} ight.. Khi đó \lim_{x ightarrow 1^{-}}f(x) = - \infty. Sai||Đúng

    Đáp án là:

    Kiểm tra sự đúng sai của các kết luận sau?

    a) Có hai trong ba hàm số y = \sin;y =\cos\sqrt{x};y = \tan x liên tục trên tập số thực. Sai||Đúng

    b) \lim_{x ightarrow - \infty}\left( \sqrt{x^{2} + 1} + x - 1 ight) = - 1 Đúng||Sai

    c) Phương trình 2x^{4} - 5x^{2} + x + 1 = 0 có ít nhất hai nghiệm thuộc khoảng (0;2).Đúng||Sai

    d) Biết hàm số f\left( x ight) = \left\{ \begin{gathered} \dfrac{{{x^2} + 1}}{{1 - x}}{\text{ khi x < 1}} \hfill \\ \sqrt {2x - 2} {\text{ khi x}} \geqslant {\text{1}} \hfill \\ \end{gathered} ight.. Khi đó \lim_{x ightarrow 1^{-}}f(x) = - \infty. Sai||Đúng

    a) Ta có hàm số lượng giác liên tục trên từng khoảng xác định của nó.

    Hàm số y = \sin xác định trên tập số thực suy ra hàm số liên tục trên \mathbb{R}

    Hàm số y = \cos\sqrt{x} xác định trên D = \lbrack 0; + \infty)

    Hàm sốy = \tan x xác định trên D\mathbb{= R}\backslash\left\{ \frac{\pi}{2} + k\pi|k\mathbb{\in Z} ight\}

    Vậy chỉ có suy nhất một hàm số liên tục trên tập số thực.

    b) Ta có:

    \lim_{x ightarrow - \infty}\left( \sqrt{x^{2} + 1} + x - 1 ight) = \lim_{x ightarrow - \infty}\left( \sqrt{x^{2} + 1} + x ight) - \lim_{x ightarrow - \infty}1

    = \lim_{x ightarrow - \infty}\left( \frac{1}{\sqrt{x^{2} + 1} - x} ight) - 1 = \lim_{x ightarrow - \infty}\left( \frac{\frac{1}{x}}{- \sqrt{1 + \frac{1}{x}} - 1} ight) - 1 = - 1

    c) Xét hàm số 2x^{4} - 5x^{2} + x + 1 = f(x) liên tục trên \mathbb{R}

    Ta có: \left\{ \begin{matrix} f( - 2) = 11;f( - 1) = - 3 \\ f(0) = 1;f(1) = - 1;f(2) = 15 \\ \end{matrix} ight.

    Vì \left\{ \begin{matrix} f(0).f( - 1) < 0 \\ f(1).f(2) < 0 \\ \end{matrix} ight. nên phương trình đã cho có ít nhất hai nghiệm thuộc khoảng (0;2).

    d) Ta có: \left\{ \begin{matrix} \lim_{x ightarrow 1^{-}}\left( x^{2} + 1 ight) = 2 > 0 \\ \lim_{x ightarrow 1^{-}}(1 - x) = 0 \\ \end{matrix} ight.. Khi x ightarrow 1^{-} \Leftrightarrow x < 1 \Leftrightarrow 1 - x > 0

    \lim_{x ightarrow 1^{-}}f(x) = \lim_{x ightarrow 1^{-}}\frac{x^{2} + 1}{1 - x} = + \infty.

  • Câu 28: Vận dụng cao

    Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tam giác SAB. Tìm điều kiện của AB và CD để thiết diện của (GIJ) với hình chóp S.ABCD là hình bình hành.

    Hình vẽ minh họa

    Tìm điều kiện của AB và CD thỏa mãn yêu cầu bài toán

    Ta có ABCD là hình thang và I, J là trung điểm của AD và BC nên IJ là đường trung bình của hình thang ABCD

    => IJ // AB // CD

    => Trong (SAB) qua G kẻ MN // AB (M ∈ SA, N ∈ SB)

    => (SAB) ∩ (IJG) = MN và MN // IJ // AB // CD

    Dễ thấy thiết diện của (IJG) và hình chóp là hình thang MNJI.

    G là trọng tâm của tam giác SAB và MN // AB nên theo định lí Ta - lét ta có:

    \frac{{MN}}{{AB}} = \frac{{SG}}{{SE}} = \frac{2}{3} (Với E là trung điểm của AB)

    => MN = \frac{2}{3}AB

    Ta lại có: IJ là đường trung bình của hình thang ABCD nên: IJ = \frac{{AB + CD}}{2}

    Để hình thang MNIJ trở thành hình bình hành thì điều kiện cần là MN = IJ

    \begin{matrix} \dfrac{2}{3}AB = \dfrac{1}{2}\left( {AB + CD} ight) \hfill \\ \Leftrightarrow \dfrac{1}{6}AB = \dfrac{1}{2}CD \hfill \\ \Leftrightarrow AB = 3CD \hfill \\ \end{matrix}

  • Câu 29: Vận dụng

    Cho dãy số \left( u_{n} ight) với u_{n} = \sqrt{2} + \left( \sqrt{2} ight)^{2} + ... + \left( \sqrt{2} ight)^{n}. Chọn mệnh đề đúng trong các mệnh đề dưới đây?

    Ta có:

    \sqrt{2};\left( \sqrt{2} ight)^{2};...;\left( \sqrt{2} ight)^{n}lập thành một cấp số nhân có nên

    u_{n} = \sqrt{2}.\frac{1 - \left( \sqrt{2} ight)^{n}}{1 - \sqrt{2}}

    = \left( 2 - \sqrt{2} ight).\left\lbrack \left( \sqrt{2} ight)^{n} - 1 ightbrack

    \Rightarrow \lim u_{n} = + \infty vì \left\{ \begin{matrix} a = 2 - \sqrt{2} > 0 \\ q = \sqrt{2} > 1 \\ \end{matrix} ight.

  • Câu 30: Thông hiểu

    Cho một cấp số nhân có các số hạng đều không âm thỏa mãn {u_2} = 6;{u_4} = 24. Tính tổng của 12 số hạng đầu tiên của cấp số nhân đó.

    Giả sử công bội của cấp số nhân là q

    Ta có:

    => {u_4} = {u_2}.{q^2} \Rightarrow q = \pm 2

    Do cấp số nhân có các số hạng không âm nên q = 2

    Ta có: {S_{12}} = {u_1}.\frac{{1 - {2^{12}}}}{{1 - 2}} = 3\left( {{2^{12}} - 1} ight)

  • Câu 31: Nhận biết

    Tìm số hạng thứ 11 của cấp số cộng có số hạng đầu bằng 3 và công sai d = −2?

    Ta có: u_{11} = u_{1} + 10d = - 17

  • Câu 32: Nhận biết

    Dùng quy nạp chứng minh mệnh đề chứa biến A(n) đúng với mọi số tự nhiên n ≥ p (p là một
    số tự nhiên). Ở bước 1 (bước cơ sở) của chứng minh quy nạp, bắt đầu với n bằng:

    Ở bước 1 (bước cơ sở) của chứng minh quy nạp, bắt đầu với n bằng n=p

  • Câu 33: Thông hiểu

    Đồ thị hàm số y = sinx được suy ra từ đồ thị C của hàm số y = cosx bằng cách.

    Ta có: y = \sin x = \cos\left( \frac{\pi}{2} - x ight) = \cos\left( x - \frac{\pi}{2} ight)

    => Đồ thị hàm số y = sinx được suy ra từ đồ thị C của hàm số y = cosx bằng cách tịnh tiến C qua phải một đoạn có độ dài là \frac{\pi}{2}

  • Câu 34: Thông hiểu

    Chọn khẳng định sai trong các khẳng định sau.

    Khẳng định sai là: “Một mặt phẳng hoàn toàn xác định khi biết nó đi qua ba điểm.”

    Sửa lại: “Một mặt phẳng hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.”

  • Câu 35: Vận dụng cao

    Tổng S = sin(x) + sin(2x) + … + sin(nx) (với x ≠ kπ ) có công thức thu gọn là?

    Ta có 2sin\frac{x}{2} \cdot S = 2sinx\cdot sin\frac{x}{2} + 2sin2x \cdot sin\frac{x}{2} + .. + 2sinnx \cdotsin\frac{x}{2}

    = \cos\frac{x}{2} - \cos\frac{3x}{2} +\cos\frac{3x}{2} - \cos{x\frac{5x}{2}} + \ldots + \cos{x\frac{2n -1}{2}x} - \cos{\frac{2n + 1}{2}x}

    = cos\frac{x}{2} - cos\frac{2n +1}{2}x

    Vậy S = \frac{cos\frac{x}{2} - cos\frac{2n+ 1}{2}x}{2sin\frac{x}{2}}

  • Câu 36: Nhận biết

    Khẳng định nào sau đây đúng?

    Ta có:

    \sin(2018a) =2\sin(1009a).\cos(1009a)

  • Câu 37: Nhận biết

    Cho dãy số (u_{n}), biết {u_n} = \frac{{2{n^2} - 1}}{{{n^2} + 3}}. Tìm số hạng u_{5}

    Ta có:

    {u_5} = \frac{{{{2.5}^2} - 1}}{{{5^2} + 3}} = \frac{{49}}{{28}} = \frac{7}{4}

  • Câu 38: Nhận biết

    Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

    Đáp án \left\{ \begin{matrix} a//b \\ b//(\alpha) \\ \end{matrix} ight.\ \Rightarrow a//(\alpha) sai: Trường hợp a \subset (\alpha).

    Đáp án \left\{ \begin{matrix} a//b \\ b \subset (\alpha) \\ \end{matrix} ight.\ \Rightarrow a//(\alpha) sai: Trường hợp a \subset (\alpha).

    Đáp án \left\{ \begin{matrix} a//(\alpha) \\ b \subset (\alpha) \\ \end{matrix} ight.\ \Rightarrow a//b sai: Trường hợp a,b chéo nhau.

  • Câu 39: Thông hiểu

    Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Xét tính đúng sai của các mệnh đề sau:

    a) AD//(ABF). Sai||Đúng

    b) (AFD)//(BEC). Đúng||Sai

    c) (ABD)//(EFC). Sai||Đúng

    d) Sáu điểm A,B,C,D,E,F là 6 đỉnh của một hình lăng trụ tam giác. Đúng||Sai

    Đáp án là:

    Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Xét tính đúng sai của các mệnh đề sau:

    a) AD//(ABF). Sai||Đúng

    b) (AFD)//(BEC). Đúng||Sai

    c) (ABD)//(EFC). Sai||Đúng

    d) Sáu điểm A,B,C,D,E,F là 6 đỉnh của một hình lăng trụ tam giác. Đúng||Sai

    Hình vẽ minh họa

    a) Sai: AD và (ABF) cắt nhau tại A.

    b) Đúng.

    Vì ABCD là hình bình hành nên AD \parallel BC, suy ra AD \parallel (BEC).

    Vì ABEF là hình bình hành nên AF \parallel BE, suy ra AF \parallel (BEC).

    Mà ADvà AFcắt nhau nên (AFD) \parallel (BEC).

    c) Sai: Vì (ABD) và (EFC) có điểm C chung.

    d) Đúng:

    Vì ABCD và ABEF là hình bình hành nên AB,\ CD,\ FE đôi một song song

    Mặt khác (AFD) \parallel (BEC) (theo câu b)

    Do đó 6 điểm A,B,C,D,E,F là 6 đỉnh của một hình lăng trụ tam giác

  • Câu 40: Thông hiểu

    Cho hàm số f(x) = \frac{x - 2}{3 - x}. Mệnh đề nào sau đây đúng?

    Ta có: \left\{ {\begin{array}{*{20}{c}} {\mathop {\lim }\limits_{x \to {3^ + }} \left( {x - 2} ight) = 1 > 0} \\ \begin{gathered} \mathop {\lim }\limits_{x \to {3^ + }} \left( {3 - x} ight) = 0 \hfill \\ x \mapsto {3^ + } \Rightarrow \left( {3 - x} ight) < 0 \hfill \\ \end{gathered} \end{array}} ight. \Rightarrow \mathop {\lim }\limits_{x \to {3^ + }} f\left( x ight) = - \infty

    \lim_{x ightarrow - \infty}f(x) =\lim_{x ightarrow - \infty}\dfrac{x - 2}{3 - x} = \lim_{x ightarrow -\infty}\dfrac{1 - \dfrac{2}{x}}{\dfrac{3}{x} - 1} = - 1

    Vậy đáp án đúng là \left\{ \begin{gathered} \mathop {\lim }\limits_{x \to {3^ + }} f\left( x ight) = - \infty \hfill \\ \mathop {\lim }\limits_{x \to + \infty } f\left( x ight) = - 1 \hfill \\ \end{gathered} ight.

  • Câu 41: Vận dụng

    Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dải), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).

    Kí hiệu p_{n} là chu vi của hình vuông thứ n và Q_{n} là tổng chu vi của n hình vuông đầu tiên. Viết công thức tính p_{n} và Q_{n}(n = 1,2,3,\ldots) và tìm lim Q_{n} (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông).

    Đáp án: 13,66

    Đáp án là:

    Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dải), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).

    Kí hiệu p_{n} là chu vi của hình vuông thứ n và Q_{n} là tổng chu vi của n hình vuông đầu tiên. Viết công thức tính p_{n} và Q_{n}(n = 1,2,3,\ldots) và tìm lim Q_{n} (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông).

    Đáp án: 13,66

    Ta có:

    p_{n} = 4 \cdot \frac{1}{(\sqrt{2})^{n - 1}}

    Q_{n} = 4 + 4 \cdot \frac{1}{\sqrt{2}} + 4 \cdot \frac{1}{(\sqrt{2})^{2}} + \ldots + 4 \cdot \frac{1}{(\sqrt{2})^{n - 1}}

    = 4 \cdot \frac{1}{1 - \frac{1}{\sqrt{2}}} \approx 13,66

  • Câu 42: Thông hiểu

    Cho cấp số nhân \frac{1}{2};\frac{1}{4};\frac{1}{8};...;\frac{1}{4096}. Hỏi số \frac{1}{4096} là số hạng thứ mấy trong cấp số nhân đã cho?

    Ta có: \frac{1}{2};\frac{1}{4};\frac{1}{8};...;\frac{1}{4096} là cấp số nhân với \left\{ \begin{matrix}u_{1} = \dfrac{1}{2} \\q = \dfrac{u_{2}}{u_{1}} = \dfrac{1}{2} \\\end{matrix} ight.

    \Rightarrow u_{n} = \frac{1}{2}.\left( \frac{1}{2} ight)^{n - 1} = \frac{1}{2^{n}} = \frac{1}{4096}

    \Rightarrow \frac{1}{2^{n}} = \frac{1}{2^{12}} \Rightarrow n = 12

  • Câu 43: Vận dụng

    Cho hàm số f(x) = \left\{ \begin{matrix}\dfrac{\sqrt{5x - 1} - \sqrt[3]{x^{2} + x + 6}}{1 - x}\ ,x > 1 \\ax + 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x \leq 1 \\\end{matrix} ight.. Tìm a để hàm số liên tục tại x = 1

    Đáp án: -3||- 3

    Đáp án là:

    Cho hàm số f(x) = \left\{ \begin{matrix}\dfrac{\sqrt{5x - 1} - \sqrt[3]{x^{2} + x + 6}}{1 - x}\ ,x > 1 \\ax + 2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x \leq 1 \\\end{matrix} ight.. Tìm a để hàm số liên tục tại x = 1

    Đáp án: -3||- 3

    Xét \lim_{x ightarrow 1^{+}}f(x) = \lim_{x ightarrow 1^{+}}\frac{\sqrt{5x - 1} - \sqrt[3]{x^{2} + x + 6}}{1 - x}

    = \lim_{x ightarrow1^{+}}\frac{\sqrt{5x - 1} - 2 + 2 - \sqrt[3]{x^{2} + x + 6}}{1 -x}

    = \lim_{x ightarrow 1^{+}}\left(\frac{\sqrt{5x - 1} - 2}{1 - x} + \frac{2 - \sqrt[3]{x^{2} + x + 6}}{1 -x} ight)

    = \lim_{x ightarrow 1^{+}}\left( \frac{5x - 5}{(1 -x)\left( \sqrt{5x - 1} + 2 ight)} + \frac{8 - \left( x^{2} + x + 6ight)}{(1 - x)\left( 4 + 2\sqrt[3]{x^{2} + x + 6} + \left(\sqrt[3]{x^{2} + x + 6} ight)^{2} ight)} ight)

    = \lim_{xightarrow 1^{+}}\left( \frac{- 5}{\left( \sqrt{5x - 1} + 2 ight)} +\frac{x + 2}{4 + 2\sqrt[3]{x^{2} + x + 6} + \left( \sqrt[3]{x^{2} + x +6} ight)^{2}} ight)

    = - \frac{5}{4} + \frac{1}{4} = - 1

    \lim_{x ightarrow 1^{-}}f(x) = \lim_{x ightarrow 1^{-}}(ax + 2) = a + 2

    f(1) = a + 2

    Hàm số liên tục tại x = 1

    \Leftrightarrow \lim_{x ightarrow 1^{+}}f(x) = \lim_{x ightarrow 1^{-}}f(x) = f(1)

    \Leftrightarrow a + 2 = - 1 \Leftrightarrow a = - 3.

  • Câu 44: Thông hiểu

    Tìm tập xác định D của hàm số y = \frac{1}{{\sqrt {1 - \sin \,x} }}.

    Hàm số xác định khi và chỉ khi 

    1 - \sin x > 0 \Leftrightarrow \sin x < 1 \,\,(*)

    Mà - 1 \leqslant \sin x \leqslant 1 nên \left( * ight) \Leftrightarrow \sin x e 1 \Leftrightarrow x e \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}

    Vậy tập xác định {\text{D}} = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} ight\}

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 11 Cánh Diều Đề 1 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án
Làm lại
  • 4 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi học kì 1 Toán 11 Cánh Diều Đề 1
Thời gian còn lại 90:00 Số câu đã làm 0/44
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập