Lớp 11 Toán 11 - Chân trời sáng tạo

Đề thi học kì 1 Toán 11 Chân trời sáng tạo Đề 3

Mô tả thêm: Đề thi HK1 Toán 11 được biên soạn gồm các câu hỏi trắc nghiệm thuộc 5 chuyên đề với 4 mức độ giúp học sinh củng cố, nắm vững kiến thức và khả năng giải toán lớp 11 sách Chân trời sáng tạo
  • Thời gian làm: 90 phút
  • Số câu hỏi: 45 câu
  • Số điểm tối đa: 45 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Mua gói để Làm bài
  • Câu 1: Vận dụng

    Cho cấp số nhân (un) có {S_2} = 4;{S_3} = 13. Biết {u_2} < 0. Tính {S_5}?

    Ta có:

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {{S_2} = 4} \\ {{S_3} = 13} \end{array}} ight. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\dfrac{{{u_1}\left( {1 - {q^2}} ight)}}{{1 - q}} = 4} \\ {\dfrac{{{u_1}\left( {1 - {q^3}} ight)}}{{1 - q}} = 13} \end{array}} ight. \hfill \\ \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{u_1}\left( {1 + q} ight) = 4} \\ {{u_1}\left( {1 + q + {q^2}} ight) = 13} \end{array}} ight. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\dfrac{{1 + q}}{{1 + q + {q^2}}} = \dfrac{4}{{13}}\left( * ight)} \\ {{u_1} = \dfrac{4}{{1 + q}}\left( {**} ight)} \end{array}} ight. \hfill \\ \end{matrix}

    Xét (*)

    \begin{matrix} \dfrac{{1 + q}}{{1 + q + {q^2}}} = \dfrac{4}{{13}}a \hfill \\ \Leftrightarrow 4{q^2} - 9q - 9 = 0 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {q = 3 \Rightarrow {u_1} = 1 \Rightarrow {u_2} = {u_1}.q = 3 > 0\left( L ight)} \\ {q = - \dfrac{3}{4} \Rightarrow {u_1} = 16 \Rightarrow {u_2} = {u_1}.q = - 12 < 0\left( {tm} ight)} \end{array}} ight. \hfill \\ \Rightarrow {S_5} = \dfrac{{{u_1}\left( {1 - {q^5}} ight)}}{{1 - q}} = \dfrac{{16.\left[ {1 - {{\left( {\dfrac{{ - 3}}{4}} ight)}^5}} ight]}}{{1 + \dfrac{3}{4}}} = \dfrac{{181}}{{16}} \hfill \\ \end{matrix}

  • Câu 2: Thông hiểu

    Cho cấp số cộng \left( u_{n} ight) có u_{1} = \frac{1}{4};d = - \frac{1}{4}. Gọi S_{5} là tổng 5 số hạng đầu tiên của cấp số cộng đã cho. Mệnh đề nào sau đây đúng?

    Ta có: \left\{ \begin{matrix}u_{1} = \dfrac{1}{4} \\d = - \dfrac{1}{4} \\\end{matrix} ight.

    Và S_{n} = n.u_{1} + \frac{n(n - 1)d}{2}

    \Leftrightarrow S_{5} = 5u_{1} + \frac{5.4.d}{2}

    \Leftrightarrow S_{5} = 5.\frac{1}{4} + 10.\left( - \frac{1}{4} ight) = - \frac{5}{4}

  • Câu 3: Vận dụng

    Tìm chu kì T của hàm số y = 2\sin^{2}x +3\cos^{2}3x

    Ta có:

    \begin{matrix}y = 2\sin^{2}x + 3\cos^{2}3x \hfill \\= 2.\dfrac{1 - \cos2x}{2} + 3.\dfrac{1 + \cos6x}{2} \hfill\\= \dfrac{1}{2}(3.\cos6x - 2\cos2x + 5)\hfill \\\end{matrix}

    Hàm số y = 3.\cos6x tuần hoàn với chu kì T_{1} = \frac{\pi}{3}

    Hàm số y = - 2\cos2x tuần hoàn với chu kì T_{2} = \pi

    T là chu kì của hàm số y = \tan3x + \cot{x} là bội chung nhỏ nhất của T1 và T2

    Suy ra hàm số y = \dfrac{1}{2}(3.\cos6x -2\cos2x + 5) tuần hoàn với chu kì T = \pi

  • Câu 4: Vận dụng

    Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M là trung điểm của AB, N là tâm hình vuông AA'D'D. Xác định các giao tuyến của hình lập phương ABCD.A'B'C'D' tạo với mặt phẳng (CMN). Tính diện tích hình tạo bởi các giao tuyến.

    Hình vẽ minh họa

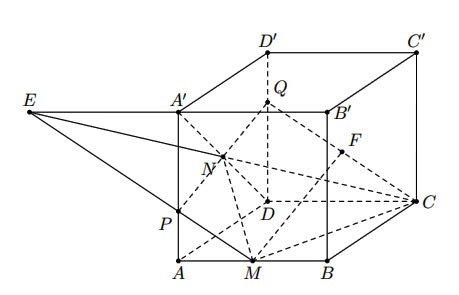
    Tính diện tích hình tạo bởi các giao tuyến

    Hình tạo bởi các giao tuyến được biểu diễn như hình vẽ.

    Tứ giác CQPM là hình thang có

    CM = \frac{a\sqrt{5}}{2};OM =\frac{a\sqrt{13}}{6};PQ = \frac{a\sqrt{10}}{3};CQ =\frac{a\sqrt{13}}{3}

    \Rightarrow MF = PQ =\frac{a\sqrt{10}}{3};CF = PM = \frac{a\sqrt{13}}{6}

    Ta có: S_{CMPQ} = 3S_{CMF}

    S_{CMF} = \sqrt{p(p - CM)(p - CF)(p -MF)} với p = \frac{CM + MF +FC}{2}

    Thay giá trị các cạnh ta có S_{CMF} =\sqrt{\frac{7}{72}}a^{2} \Rightarrow S_{CMPQ} =\frac{a^{2}\sqrt{14}}{4}

  • Câu 5: Vận dụng

    Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tam giác SAB. Tìm giao tuyến của MA và SD.

    Hình vẽ minh họa:

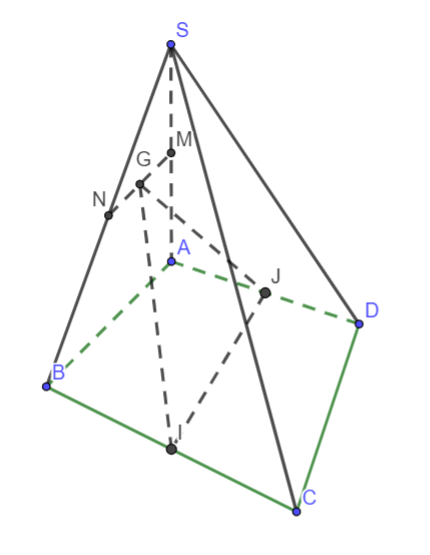
    Tìm giao tuyến của MA và SD

    Xét hình thang ABCD có I và J lần lượt là trung điểm của AD; BC nên:

    IJ là đường trung bình hình thang ABCD => IJ // AB

    Hai mặt phẳng (GIJ) và (SAB): lần lượt chứa hai đường thẳng song song (là IJ và AB) và có điểm G chung

    => Giao tuyến của chúng là đường thẳng đi qua G và song song với AB.

    Đường thẳng này cắt SA tại M và cắt SB tại N.

  • Câu 6: Nhận biết

    Cho dãy số \left( u_{n} ight) với u_{n} = \frac{4^{n - 1}}{5^{n - 2}}. Tính \lim_{n ightarrow + \infty}u_{n}.

    Ta có:

    \lim_{n ightarrow + \infty}u_{n} = \lim_{n ightarrow + \infty}\frac{4^{n - 1}}{5^{n - 2}} = \lim_{n ightarrow + \infty}\left( \left( \frac{4}{5} ight)^{n}.\frac{4^{- 1}}{5^{- 2}} ight) = 0

  • Câu 7: Vận dụng cao

    Cho dãy số \left( u_{n} ight) biết \left\{ \begin{matrix} u_{1} = 2 \\ u_{n + 1} = 2u_{n - 1} + 3;(n \geq 2) \\ \end{matrix} ight.. Số hạng có ba chữ số lớn nhất của dãy là:

    Tìm số hạng tổng quát của dãy số

    Dự đoán u_{n} = 5.2^{n - 1} - 3;(n \geq 2)

    Ta chứng minh theo phương pháp quy nạp

    Với n = 1 ta có: u_{2} = 5.2 - 3 = 7(tm)

    Giả sử u_{k} = 5.2^{k - 1} - 3, khi đó ta có:

    u_{k + 1} = 2u_{k} + 3

    = 2\left( 5.2^{k - 1} - 3 ight) + 3

    = 5.2^{k} - 3

    Vậy công thức tổng quát được chứng minh theo nguyên lí quy nạp.

    Ta có: u_{n} < 1000 \Rightarrow 2^{n - 1} < \frac{1003}{5} = 200,6

    Mà 2^{7} = 128;2^{8} = 256

    Nên ta chọn 2^{n - 1} = 2^{7} \Rightarrow n = 8

    Vậy u_{8} là số hạng cần tìm.

  • Câu 8: Thông hiểu

    Mệnh đề nào sau đây đúng?

    Mệnh đề “Nếu ba đường thẳng đồng quy thì chúng nằm trên một mặt phẳng” không đúng, vì chúng có thể không đồng phẳng.

    Mệnh đề “Nếu một đường thẳng cắt hai đường thẳng cho trước thì cả ba đường thẳng cùng nằm trong một mặt phẳng”, không đúng khi ba đường thẳng cắt nhau và đồng qui nhưng không đồng phẳng.

    Mệnh đề “Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cũng cắt đường thẳng còn lại” không đúng, vì chúng có thể chéo nhau.

    Vậy khẳng định đúng là: “Nếu một đường thẳng cắt hai đường thẳng cắt nhau tại hai điểm phân biệt thì cả ba đường thẳng cùng nằm trong một mặt phẳng.”

  • Câu 9: Vận dụng

    Tìm tần số còn thiếu trong mẫu dữ liệu ghép nhóm dưới đây. Biết số trung bình bằng 19,92?

    Đối tượng

    Tần số

    [4; 8)

    11

    [8; 12)

    13

    [12; 16)

    16

    [16; 20)

    14

    [20; 24)

    a

    [24; 28)

    9

    [28; 32)

    17

    [32; 36)

    6

    [36; 40)

    4

    Ta có:

    Giá trị đại diện

    Tần số

    Tích các giá trị

    6

    11

    66

    10

    13

    130

    14

    16

    224

    18

    14

    252

    22

    a

    22a

    26

    9

    234

    30

    17

    510

    34

    6

    204

    38

    4

    152

    Tổng

    90 + a

    1772 + 22a

    Biết số trung bình bằng  19,92  nên ta có:

    \overline{x} = 19,92

    \Leftrightarrow \frac{1772 + 22a}{90 +a} = 19,92

    \Leftrightarrow a = 10

  • Câu 10: Nhận biết

    Hàm số nào sau đây không liên tục tại x = 2?

    Hàm số y = \frac{x^{2}}{x - 2} có tập xác định D\mathbb{= R}\backslash\left\{ 2 ight\} nên không liên tục tại x = 2.

  • Câu 11: Thông hiểu

    Cho một cấp số cộng \left( u_{n} ight) có u_{1} = 2;u_{8} = 16. Tìm d;S_{10}?

    Theo bài ra ta có:

    \left\{ \begin{matrix} u_{1} = 2 \\ u_{8} = 16 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} u_{1} = 2 \\ u_{1} + 7d = 16 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} u_{1} = 2 \\ d = 2 \\ \end{matrix} ight.

    \Rightarrow S_{10} = \frac{\left\lbrack 2u_{1} + 9d ightbrack.n}{2} = 110

  • Câu 12: Vận dụng cao

    Gọi M,\ m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y =sin^{2}x - 4sinx + 5. Tính P = M -2m^{2}.

    Ta có: 

    y = sin^{2}x - 4sinx + 5 = \left(\sin x - 2 ight)^{2} + 1.

    Do - 1 \leq \sin x \leq 1

    \begin{matrix}\Leftrightarrow - 3 \leq \sin x - 2 \leq - 1 \\\Leftrightarrow 1 \leq \left( \sin x - 2 ight)^{2} \leq 9 \\\end{matrix}

    \begin{matrix}\Leftrightarrow 2 \leq \left( \sin x - 2 ight)^{2} + 1 \leq 10 \hfill\\\Leftrightarrow \left\{ \begin{matrix}M = 10 \\m = 2 \hfill\\\end{matrix} ight.\ \hfill \\\Leftrightarrow P = M - 2m^{2} = 2.\hfill \\\end{matrix}

  • Câu 13: Thông hiểu

    Tìm trung vị của mẫu số liệu ghép nhóm sau đây:

    Thời gian (s)

    Số vận động viên (người)

    (50,5; 55,5]

    2

    (55,5; 60,5]

    7

    (60,5; 65,5]

    8

    (65,5; 70,5]

    4

    Ta có:

    Thời gian (s)

    Số vận động viên (người)

    Tần số tích lũy

    (50,5; 55,5]

    2

    2

    (55,5; 60,5]

    7

    9

    (60,5; 65,5]

    8

    17

    (65,5; 70,5]

    4

    21

    Tổng

    N = 21

     

    Ta có: \frac{N}{2} = \frac{21}{2} =10,5

    => Nhóm chứa trung vị là (60,5; 65,5]

    Khi đó: \left\{ \begin{matrix}l = 60,5,\dfrac{N}{2} = 10,5 \\m = 9,f = 8,d = 65,5 - 60,5 = 5 \\\end{matrix} ight.

    Trung vị của mẫu số liệu là:

    M_{e} = L + \dfrac{\dfrac{N}{2} -m}{f}.d

    \Rightarrow M_{e} = 60,5 + \frac{10,5 -9}{8}.5 \approx 61,4

  • Câu 14: Vận dụng cao

    Cho hình chóp S.ABCD có đáy ABCD là hình thang; AB = 2CD,\ \ AB \parallel CD. M là trung điểm của cạnh AD; mặt phẳng (\alpha) qua Mvà song song với mp(SAB) cắt hình chóp S.ABCD theo một thiết diện là hình (H). Biết S_{(H)} = xS_{\Delta SAB}. Giá trị của x là:

    Đáp án: 0,5 (Kết quả ghi dưới dạng số thập phân)

    Đáp án là:

    Cho hình chóp S.ABCD có đáy ABCD là hình thang; AB = 2CD,\ \ AB \parallel CD. M là trung điểm của cạnh AD; mặt phẳng (\alpha) qua Mvà song song với mp(SAB) cắt hình chóp S.ABCD theo một thiết diện là hình (H). Biết S_{(H)} = xS_{\Delta SAB}. Giá trị của x là:

    Đáp án: 0,5 (Kết quả ghi dưới dạng số thập phân)

    Hình vẽ minh họa

    Gọi N,P,Q lần lượt là trung điểm các cạnh SD,SC,BC.

    Gọi E = AD \cap BC,I = MN \cap PQ ta có S,I,E thẳng hàng vì cùng thuộc giao tuyến của (SAD) và (SBC).

    Thiết diện là hình thang MNPQ (vì NP \parallel AB \parallel MQ).

    Ta có S_{MNPQ} = S_{\Delta IMQ} - S_{\Delta INP}, mà \frac{NP}{DC} = \frac{1}{2},\frac{DC}{MQ} = \frac{2}{3} \Rightarrow \frac{NP}{MQ} = \frac{1}{3}

    \Rightarrow S_{\Delta INP} = \frac{1}{9}S_{\Delta IMQ}

    \Rightarrow S_{MNPQ} = S_{\Delta IMQ} - \frac{1}{9}S_{\Delta IMQ} = \frac{8}{9}S_{\Delta IMQ}.

    Ta có M là trung điểm AD, D là trung điểm của AE nên \frac{MI}{SA} = \frac{3}{4}

    \Rightarrow S_{\Delta IMQ} = \frac{9}{16}S_{\Delta SAB}

    \Rightarrow S_{MNPQ} = \frac{8}{9}.\frac{9}{16}S_{\Delta SAB} = \frac{1}{2}S_{\Delta SAB}.

  • Câu 15: Nhận biết

    Dãy số nào là dãy số tăng?

    Xét u_{n} = n^{2} ta có: u_{n + 1} - u_{n} = (n + 1)^{2} - n^{2} = 2n + 1 > 0;\forall n \in \mathbb{N}^{*}

    Vậy u_{n} = n^{2} là dãy số tăng.

  • Câu 16: Nhận biết

    Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?

    Hình vẽ minh họa

    Với 4 điểm không đồng phẳng A,B,C,D có thể xác định được 4 mặt phẳng phân biệt từ các điểm đó là (ABC),(BCD),(ACD),(ABD).

  • Câu 17: Thông hiểu

    Điểm kiểm tra môn Toán của học sinh lớp 11A được ghi trong bảng sau:

    Điểm

    Số học sinh

    [20; 30)

    4

    [30; 40)

    6

    [40; 50)

    15

    [50; 60)

    12

    [60; 70)

    10

    [70; 80)

    6

    [80; 90)

    4

    [90; 100]

    3

    Biết rằng nếu học sinh có ít nhất 60 điểm và không vượt quá 80 điểm sẽ đạt điểm B. Hỏi phần trăm số học sinh đạt điểm B trong lớp 11A chiếm bao nhiêu phần trăm?

    Quan sát bảng số liệu ghép nhóm ta thấy:

    Số học sinh lớp 11A là 60 học sinh

    Nhóm [60; 70) có 10 học sinh

    Nhóm [70; 80) có 6 học sinh

    => Số học sinh đạt điểm B là 10 + 6 = 16 (học sinh)

    Vậy số học sinh đạt điểm B chiếm \frac{16}{60}.100\% \approx 26,7\%

  • Câu 18: Thông hiểu

    Cho dãy số \left( u_{n} ight) có số hạng tổng quát u_{n} = \frac{( - 1)^{n}}{1 + n}. Khẳng định nào sau đây sai?

    Ta có:

    u_{1} = - \frac{1}{2};u_{2} = \frac{1}{3};u_{3} = - \frac{1}{4}

    \Rightarrow \left\{ \begin{matrix} u_{1} < u_{2} \\ u_{2} > u_{3} \\ \end{matrix} ight.

    Vậy dãy số đã cho không tăng không giảm.

    Khẳng định sai là: “Dãy số \left( u_{n} ight) là dãy giảm”

  • Câu 19: Nhận biết

    Cho hình vẽ:

    Trên đường tròn lượng giác, số đo của góc lượng giác (OA;OB') là:

    Từ hình vẽ ta có: (OA;OB') = - \frac{\pi}{2}

  • Câu 20: Vận dụng cao

    Nếu \tan\alpha và \tan\beta là hai nghiệm của phương trình x^{2} - px + q = 0;(q eq 0) thì P = cos^{2}(\alpha + \beta) + p\sin(\alpha + \beta).cos(\alpha + \beta) + qsin^{2}(\alpha + \beta) bằng:

    Ta có: \tan\alpha và \tan\beta là hai nghiệm của phương trình x^{2} - px + q = 0;(q eq 0)nên theo định lí Vi – ét ta có: \left\{ \begin{matrix} \tan\alpha + \tan\beta = p \\ \tan\alpha.tan\beta = q \\ \end{matrix} ight.

    \Rightarrow \tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha.tan\beta} = \frac{p}{1 - q}

    Khi đó:

    P = \cos^{2}(\alpha + \beta) +p\sin(\alpha + \beta).\cos(\alpha + \beta) + q\sin^{2}(\alpha +\beta)

    P = \cos^{2}(\alpha + \beta).\left\lbrack1 + p\tan(\alpha + \beta) + q\tan^{2}(\alpha + \beta)ightbrack

    P = \frac{1 + p\tan(\alpha + \beta) +q\tan^{2}(\alpha + \beta)}{1 + \tan^{2}(\alpha + \beta)}

    P = \dfrac{1 + p.\dfrac{p}{1 - q} +q.\left( \dfrac{p}{1 - q} ight)^{2}}{1 + \left( \dfrac{p}{1 - q}ight)^{2}}

    P = \dfrac{(1 - q)^{2} + p^{2}(1 - q) +q.p^{2}}{(1 - q)^{2} + p^{2}}

    P = \dfrac{(1 - q)^{2} + p^{2} - p^{2}.q+ q.p^{2}}{(1 - q)^{2} + p^{2}}

    P = 1

  • Câu 21: Nhận biết

    Trong các đẳng thức sau, đẳng thức nào đúng?

    Công thức đúng là: sin(\alpha + \pi) = - sin\alpha

  • Câu 22: Nhận biết

    Tìm tất cả các nghiệm của phương trình \sin\left( x + \frac{\pi}{6} ight) = 1.

    Ta có \sin\left( x + \frac{\pi}{6} ight) = 1

    \Leftrightarrow x + \frac{\pi}{6} = \frac{\pi}{2} + k2\pi

    \Leftrightarrow x = \frac{\pi}{3} + k2\pi\left( k\mathbb{\in Z} ight).

  • Câu 23: Nhận biết

    Cho mặt phẳng (\alpha) và đường thẳng a\subset(\alpha). Khẳng định nào sau đây sai?

    Nếu a song song với (\alpha) và đường thẳng b \subset (\alpha) thì b và a hoặc song song với nhau hoặc chéo nhau.

  • Câu 24: Nhận biết

    Cho hai mặt phẳng (P), (Q) cắt nhau theo giao tuyến là đường thẳng d. Đường thẳng a song song với cả hai mặt phẳng (P), (Q). Khẳng định nào sau đây đúng?

    Sử dụng hệ quả: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

    Vậy a song song d

  • Câu 25: Vận dụng

    \lim_{x ightarrow 1}\frac{x^{100} - 2x + 1}{x^{50} - 2x + 1} bằng:

    Ta có:

    \lim_{x ightarrow 1}\frac{x^{100} - 2x + 1}{x^{50} - 2x + 1}

    = \lim_{x ightarrow 1}\frac{\left( x^{100} - 1 ight) - 2(x - 1)}{\left( x^{50} - 1 ight) - 2(x - 1)}

    = \lim_{x ightarrow 1}\frac{(x - 1)\left( x^{99} + x^{98} + .... + x + 1 - 2 ight)}{(x - 1)\left( x^{49} + x^{48} + .... + x + 1 - 2 ight)}

    = \lim_{x ightarrow 1}\frac{x^{99} + x^{98} + .... + x + 1 - 2}{x^{49} + x^{48} + .... + x + 1 - 2} = \frac{98}{48} = \frac{49}{24}

  • Câu 26: Nhận biết

    Cho cấp số cộng (un) có các số hạng đầu lần lượt là 5; 9; 13; 17; …. Tìm số hạng tổng quát un của cấp số cộng.

    Các số 5; 9; 13; 17; …. theo thứ tự lập thành một cấp số cộng (un) nên:

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {{u_1} = - 3} \\ {d = {u_2} - {u_1} = 4} \end{array}\mathop \to \limits^{CTTQ} } ight.{u_n} = {u_1} + \left( {n - 1} ight)d = 5 + 4\left( {n - 1} ight) = 4n + 1 \hfill \\ \Rightarrow {u_n} = 4n + 1 \hfill \\ \end{matrix}

  • Câu 27: Thông hiểu

    Giả sử tứ giác ABCD là hình biểu diễn của một tứ diện ABCD’. Nếu ABCD là một hình vuông, tìm mệnh đề đúng trong các mệnh đề sau.

    Do ABCD là hình vuông nên tam giác ABC vuông cân tại B.

    Hình biểu diễn của tứ diện ABCD’ là tứ giác ABCD nên hình biểu diễn của tam giác ABC là tam giác ABC vuông cân tại B.

  • Câu 28: Thông hiểu

    Cho hàm số f\left( x ight) = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{{x^2}}}{x}{\text{ khi }}x < 1,x e 0} \\ \begin{gathered} {\text{0 khi }}x = 0 \hfill \\ \sqrt x {\text{ khi }}x \geqslant 1 \hfill \\ \end{gathered} \end{array}} ight.. Hàm số f(x) liên tục tại:

    Tập xác định D\mathbb{= R}

    Dễ thấy hàm số y = f(x) liên tục trên mỗi khoảng ( - \infty;0),(0;1);(1; + \infty)

    Ta có:

    f(0) = 0

    \lim_{x ightarrow 0^{-}}f(x) = \lim_{x ightarrow 0^{-}}\frac{x^{2}}{x} = \lim_{x ightarrow 0^{-}}(x) = 0

    \lim_{x ightarrow 0^{+}}f(x) = \lim_{x ightarrow 0^{+}}\frac{x^{2}}{x} = \lim_{x ightarrow 0^{+}}(x) = 0

    Vậy hàm số liên tục tại x = 0

    Tương tự ta có:

    f(1) = 1

    \lim_{x ightarrow 1^{-}}f(x) = \lim_{x ightarrow 1^{-}}\frac{x^{2}}{x} = \lim_{x ightarrow 1^{-}}(x) = 1

    \lim_{x ightarrow 1^{+}}f(x) = \lim_{x ightarrow 1^{+}}\sqrt{x} = 1

    Vậy hàm số liên tục tại x = 1

    Vậy hàm số đã cho liên tục trên tập số thực.

  • Câu 29: Thông hiểu

    Tìm x để ba số 1 + x;9 + x;33 + x theo thứ tự đó lập thành một cấp số nhân.

    Ta có:

    Ba số 1 + x;9 + x;33 + x theo thứ tự đó lập thành một cấp số nhân

    \Rightarrow (9 + x)^{2} = (1 + x).(33 + x)

    \Rightarrow 81 + 18x + x^{2} = x^{2} + 34x + 33

    \Rightarrow 16x = 48

    \Rightarrow x = 3

  • Câu 30: Thông hiểu

    Cho hình chóp tứ giác S.ABCD, đáy ABCD là tứ giác lồi. Gọi O = AC \cap BD;M = AB \cap CD; N = AD \cap BC. Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD)?

    Hình vẽ minh họa

    Nhận thấy S và M lần lượt là hai điểm chung của hai mặt phẳng (SAB) và (SCD).

    Do đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là SM.

  • Câu 31: Vận dụng

    Số nghiệm của phương trình 2 \sin^{2}x-5 \sin x+3=0 thuộc \left [ 0;2\pi  ight ] là:

     Giải phương trình:

    \begin{matrix} 2{\sin ^2}x - 5\sin x + 3 = 0 \hfill \\ \Leftrightarrow \left( {\sin x - 1} ight)\left( {2\sin x - 3} ight) = 0 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {\sin x - 1 = 0} \\ {2\sin x - 3 = 0} \end{array}} ight. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {\sin x = 1} \\ {\sin x = \dfrac{3}{2}\left( L ight)} \end{array}} ight. \hfill \\ \sin x = 1 \Rightarrow x = \dfrac{\pi }{2} + k2\pi ,\left( {k \in \mathbb{Z}} ight) \hfill \\ \end{matrix}

    Ta có: x \in \left[ {0;2\pi } ight]

    \begin{matrix} \Rightarrow 0 \leqslant \dfrac{\pi }{2} + k2\pi \leqslant 2\pi \hfill \\ \Rightarrow - \dfrac{1}{4} \leqslant k \leqslant \dfrac{3}{4} \Rightarrow k = 0 \hfill \\ \end{matrix}

  • Câu 32: Vận dụng

    Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng. Độ dài các cạnh của tam giác đó là:

    Ba cạnh của một tam giác theo thứ tự là a;b;cvới a < b < c lập thành một cấp số cộng nên

    \left\{ \begin{matrix} a^{2} + b^{2} = c^{2} \\ a + b + c = 3 \\ a + c = 2b \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} a^{2} + b^{2} = c^{2} \\ 3b = 3 \\ a + c = 2b \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} a^{2} + b^{2} = c^{2} \\ b = 1 \\ a = 2b - c - 2 - c \\ \end{matrix} ight.

    Ta có:

    a^{2} + b^{2} = c^{2}\overset{b = 1}{\underset{a = 2 - c}{ightarrow}}(2 - c)^{2} + 1 = c^{2}

    \Rightarrow - 4c = 5 \Rightarrow c = \frac{5}{4}

    \Rightarrow \left\{ \begin{matrix}a = \dfrac{3}{4} \\b = 1 \\c = \dfrac{5}{4} \\\end{matrix} ight.

  • Câu 33: Thông hiểu

    Hỏi trên \left[ {0;\frac{\pi }{2}} ight), phương trình 2{\sin ^2}x - 3\sin x + 1 = 0 có bao nhiêu nghiệm?

     Phương trình 2{\sin ^2}x - 3\sin x + 1 = 0 \Leftrightarrow \left[ \begin{gathered} \sin x = \frac{1}{2} \hfill \\ \sin x = 1 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left[ \begin{gathered} \sin x = \sin \frac{\pi }{6} \hfill \\ \sin x = 1 \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = \frac{\pi }{6} + k2\pi \hfill \\ x = \frac{{5\pi }}{6} + k2\pi \hfill \\ x = \frac{\pi }{2} + k2\pi \hfill \\ \end{gathered} ight.{\text{ }}\left( {k \in \mathbb{Z}} ight)

    Theo giả thiết

    0 \leqslant x < \frac{\pi }{2} \Leftrightarrow \left[ \begin{gathered} 0 \leqslant \frac{\pi }{6} + k2\pi < \frac{\pi }{2} \hfill \\ 0 \leqslant \frac{{5\pi }}{6} + k2\pi < \frac{\pi }{2} \hfill \\ 0 \leqslant \frac{\pi }{2} + k2\pi < \frac{\pi }{2} \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left[ \begin{gathered} - \frac{1}{{12}} < k < \frac{1}{6}\xrightarrow{{k \in \mathbb{Z}}}k = 0 \to x = \frac{\pi }{6} \hfill \\ - \frac{5}{{12}} < k < - \frac{1}{{12}}\xrightarrow{{k \in \mathbb{Z}}}k \in \emptyset \hfill \\ - \frac{1}{4} < k < 0\xrightarrow{{k \in \mathbb{Z}}}k \in \emptyset \hfill \\ \end{gathered} ight.

    Vậy phương trình có duy nhất một nghiệm trên \left[ {0;\frac{\pi }{2}} ight).

  • Câu 34: Vận dụng cao

    Cho hàm số y = f(x) = ax^{3} + bx^{2} + cx + 2020. Với a eq 0,a,b,c\mathbb{\in R} và a + 2b + 4c - 8 > 0. Biết \lim_{x ightarrow - \infty}f(x) = + \infty. Hỏi đồ thị hàm số y = g(x) = a(x - 2021)^{3} + b(x - 2021)^{2} + c(x - 2021) - 1 cắt trục hoành tại bao nhiêu điểm?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) = ax^{3} + bx^{2} + cx + 2020. Với a eq 0,a,b,c\mathbb{\in R} và a + 2b + 4c - 8 > 0. Biết \lim_{x ightarrow - \infty}f(x) = + \infty. Hỏi đồ thị hàm số y = g(x) = a(x - 2021)^{3} + b(x - 2021)^{2} + c(x - 2021) - 1 cắt trục hoành tại bao nhiêu điểm?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 35: Nhận biết

    Trong các dãy số sau, dãy số nào là một cấp số nhân?

    Ta có:

    Dãy số \left( u_{n} ight) là cấp số nhân

    \Leftrightarrow u_{n} = q.u_{n - 1};\left( n \in \mathbb{N}^{*} ight)

    \Leftrightarrow \frac{u_{2}}{u_{1}} = \frac{u_{3}}{u_{2}} = \frac{u_{4}}{u_{3}} = ... = q;\left( u_{n} eq 0 ight)

    Gọi q là công bội.

    Xét đáp án 128; - 64;32; - 16;8;...

    \Leftrightarrow \frac{u_{2}}{u_{1}} = - \frac{1}{2} = \frac{u_{3}}{u_{2}} = \frac{u_{4}}{u_{3}}

    Xét đáp án \sqrt{2};2;4;4\sqrt{2};...

    \Leftrightarrow \frac{u_{2}}{u_{1}} = \frac{1}{\sqrt{2}} eq 2 = \frac{u_{3}}{u_{2}}

    Xét đáp án 5;6;7;8;...

    \Leftrightarrow \frac{u_{2}}{u_{1}} = \frac{6}{5} eq \frac{7}{6} = \frac{u_{3}}{u_{2}}

    Xét đáp án 15;5;1;\frac{1}{5};...

    \Leftrightarrow \frac{u_{2}}{u_{1}} = \frac{1}{3} eq \frac{1}{5} = \frac{u_{3}}{u_{2}}

  • Câu 36: Nhận biết

    Điều kiện xác định của hàm số y = f\left( x ight) = \frac{{2\cos x - 1}}{{\sin x}}

     Điều kiện xác định của hàm số:

    \begin{matrix} \sin x e 0 \hfill \\ \Leftrightarrow x e k\pi ,k \in \mathbb{Z} \hfill \\ \end{matrix}

  • Câu 37: Thông hiểu

    Tính giới hạn E = \lim_{x ightarrow 3^{+}}\frac{x - 3}{\sqrt{x^{2} - 9}}

    Ta có:

    E = \lim_{x ightarrow 3^{+}}\frac{x - 3}{\sqrt{x^{2} - 9}} = \lim_{x ightarrow 3^{+}}\frac{\sqrt{(x - 3)^{2}}}{\sqrt{(x - 3)(x + 3)}} = \lim_{x ightarrow 3^{+}}\frac{\sqrt{x - 3}}{\sqrt{x + 3}} = 0

  • Câu 38: Thông hiểu

    Người ta kiểm tra chiều cao của các cây thân gỗ trong rừng (đơn vị: mét), kết quả được ghi trong bảng sau:

    7,3

    7,8

    7,5

    6,6

    8,5

    8,3

    8,3

    7,5

    8,4

    8,6

    7,4

    8,2

    8,0

    8,1

    8,7

    8,2

    8,8

    8,1

    7,7

    7,8

    8,5

    7,0

    7,9

    6,9

    9,4

    9,0

    8,0

    8,7

    8,9

    7,6

    8,0

    8,2

    7,9

    7,7

    7,2

    Chuyển mẫu số liệu trên thành mẫu số liệu ghép nhóm. Biết mẫu số liệu được chia thành 6 nhóm theo các nửa khoảng có độ dài như nhau. Khi đó nhóm chiếm tỉ lên cao nhất là:

    Khoảng biến thiên: 9,4 – 6,6 = 2,8

    Ta chia thành các nhóm sau:

    \lbrack 6,5;7),\lbrack 7;7,5),\lbrack7,5;8),\lbrack 8;8,5),\lbrack 8,5;9),\lbrack 9;9,5)

    Đếm số giá trị của mỗi nhóm ta có bảng ghép nhóm như sau:

    Chiều cao (m)

    Số cây

    [6,5; 7)

    2

    [7; 7,5)

    4

    [7,5; 8)

    9

    [8; 8,5)

    11

    [8,5; 9)

    7

    [9; 9,5)

    2

    Từ bảng số liệu ta thấy nhóm chiếm tỉ lệ cao nhất là: [8,0; 8,5).

  • Câu 39: Vận dụng cao

    Số thập phân vô hạn tuần hoàn 0,353535 . . . được biểu diễn bởi phân số tối giản \frac{m}{n}. Tính P = mn

    Ta có:

    \begin{matrix} 0,353535 = 0,35 + 0,0035 + ... \hfill \\ = \dfrac{{35}}{{{{10}^2}}} + \dfrac{{35}}{{{{10}^4}}} + ... + \dfrac{{35}}{{{{10}^n}}} + ... \hfill \\ \end{matrix}

    Dãy số \frac{35}{10^{2}};\frac{35}{10^{4}};...;\frac{35}{10^{n}};... là một cấp số nhân lùi vô hạn có số hạng đầu là u_{1} = \frac{35}{10^{2}}, công sai là q = 10^{- 2}

    => S = \dfrac{u_{1}}{1 - q} =\dfrac{\dfrac{35}{10^{2}}}{1 - 10^{- 2}} = \dfrac{35}{99}

    Vậy 0,353535 = \frac{35}{99}

    \Rightarrow \left\{ \begin{matrix} m = 35 \\ n = 99 \\ \end{matrix} ight.\ \Rightarrow P = 3465

  • Câu 40: Nhận biết

    Tìm nhóm chứa mốt của mẫu dữ liệu dưới đây:

    Nhóm dữ liệu

    Tần số

    (0; 15]

    4

    (15; 30]

    12

    (30; 45]

    17

    (45; 60]

    7

    Nhóm chứa mốt là: (30; 45] vì có tần số cao nhất.

  • Câu 41: Thông hiểu

    Đồ thị hàm số y = \sin x được suy từ đồ thị (C) của hàm số bằng cách:

    Ta có

    y = \sin x = \cos \left( {\frac{\pi }{2} - x} ight) = \cos \left( {x - \frac{\pi }{2}} ight)

    =>Đồ thị hàm số y = \sin x được suy từ đồ thị (C) của hàm số bằng cách tịnh tiến (C) qua phải một đoạn có độ dài là \frac{\pi }{2}

  • Câu 42: Thông hiểu

    Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là trung điểm của các cạnh BA, BC và K là một điểm bất kỳ trên cạnh BC. Gọi I là giao điểm của EF và CD.

    a) Giao tuyến của (SEF) và (SCD) là đường thẳng SI.Đúng||Sai

    b) Giao tuyến của (EFK) và (SAC) là đường thẳng qua K và song song với EF và AC.Đúng||Sai

    c) Giao tuyến của (SBC) và (SAD) là đường thẳng qua S và song song với AD và BC. Đúng||Sai

    d) Đường thẳng AB song song với măt phẳng (SFD). Sai||Đúng

    Đáp án là:

    Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là trung điểm của các cạnh BA, BC và K là một điểm bất kỳ trên cạnh BC. Gọi I là giao điểm của EF và CD.

    a) Giao tuyến của (SEF) và (SCD) là đường thẳng SI.Đúng||Sai

    b) Giao tuyến của (EFK) và (SAC) là đường thẳng qua K và song song với EF và AC.Đúng||Sai

    c) Giao tuyến của (SBC) và (SAD) là đường thẳng qua S và song song với AD và BC. Đúng||Sai

    d) Đường thẳng AB song song với măt phẳng (SFD). Sai||Đúng

    Hình vẽ minh họa

    a) Ta có: S \in (SEF) \cap (SCD)\ \ (1)

    Trong (ABCD) có I = EF \cap CD

    \Rightarrow \left\{ \begin{matrix} I \in EF \subset (EFS) \\ I \in CD \subset (SCD) \\ \end{matrix} ight.\ \Rightarrow I \in (EFS) \cap (SCD)\ \ \ (2)

    Từ (1) và (2) suy ra SI = (SEF) \cap (SCD)

    b) Ta có: \left\{ \begin{matrix} K \in (EFK) \\ K \in SC \subset (SAC) \\ \end{matrix} ight.\ \Rightarrow K \in (EFK) \cap (SAC)

    EF//AC do EF là đường trung bình trong tam giác ABC

    \left\{ \begin{matrix} EF \subset (EFK) \\ AC \subset (SAC) \\ \end{matrix} ight.\ \Rightarrow (EFK)\bigcap(SAC) = Kx//EF//AC

    c) Chọn (SBC) chứa FK

    Ta có: \left\{ \begin{matrix} S \in (SBC) \cap (SAD) \\ BC//AD \\ BC \subset (SBC);AD \subset (SAD) \\ \end{matrix} ight.

    (SBC) \cap (SAD) = Sy//AD//BC

    d) Đường thẳng AB song song với măt phẳng (SFD) sai.

  • Câu 43: Vận dụng

    Cho hình chóp S.ABCD, đáy là hình bình hành ABCD, các điểm M, N lần lượt thuộc các cạnh AB, SC. Phát biểu nào sau đây là đúng?

    Hình vẽ minh họa

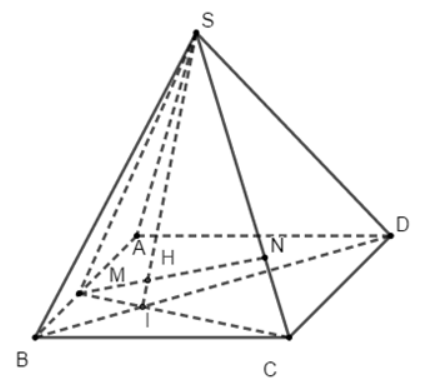
     Phát biểu nào sau đây là đúng

    Trong mặt phẳng (ABCD) gọi I là giao điểm của MC và BD.

    Trong mặt phẳng (SMC) gọi H là giao điểm của SI và MN.

    Khi đó H ∈ SI ⊂ (SBD); H ∈ MN.

    => H là giao điểm của MN và mặt phẳng (SBD).

  • Câu 44: Vận dụng

    \lim \frac{{{{( - 1)}^n}}}{{n + 5}} bằng:

    Ta có:

    0 \leqslant \left| {\frac{{{{( - 1)}^n}}}{{n + 5}}} ight| \leqslant \frac{1}{{n + 5}} < \frac{1}{n}

    Do \lim \frac{1}{n} = 0 => \lim \frac{{{{\left( { - 1} ight)}^n}}}{{n + 5}} = 0

  • Câu 45: Thông hiểu

    Đổi số đo của góc - 125^{0}45' sang đơn vị radian:

    Áp dụng công thức \mu = \frac{m.\pi}{180} với \mu tính bằng rad và m tính bằng độ.

    Ta có: - 125^{0}45' = - \left( 125 + \frac{45}{60} ight)^{0} khi đó:

    \mu = \dfrac{- \left( 125 + \dfrac{45}{60}ight)^{0}.\pi}{180} = \dfrac{503.\pi}{720}

Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 11 Chân trời sáng tạo Đề 3 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
Xem đáp án
Làm lại
  • 6 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận
Đề thi học kì 1 Toán 11 Chân trời sáng tạo Đề 3
Thời gian còn lại 90:00 Số câu đã làm 0/45
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
Chưa làm Đã làm
Làm lại Nộp bài
Đăng nhập