Tính thể tích ![]() của khối lăng trụ
của khối lăng trụ ![]() biết thể tích khối chóp
biết thể tích khối chóp ![]() bằng
bằng ![]()
Ta có thể tích khối chóp:
Suy ra:
Mời các bạn học cùng thử sức với Đề thi học kì 1 môn Toán lớp 12 nha!
Tính thể tích ![]() của khối lăng trụ
của khối lăng trụ ![]() biết thể tích khối chóp
biết thể tích khối chóp ![]() bằng
bằng ![]()
Ta có thể tích khối chóp:
Suy ra:
Cho ![]() và
và ![Q = 2\sqrt {{{\left( {\sqrt[3]{{{x^2}}} + \sqrt[3]{{{y^2}}}} ight)}^3}}](https://i.khoahoc.vn/data/image/holder.png) với x và y là các số thực khác 0. So sánh P và Q?
với x và y là các số thực khác 0. So sánh P và Q?
Ta có: là những số thực dương
Ta lại có:
Tính đạo hàm của hàm số ![]() là:
là:
Áp dụng công thức tính đạo hàm: ta có:
Cho x, y, z là ba số thực thuộc đoạn [1; 9] và ![]() . Giá trị nhỏ nhất của biểu thức
. Giá trị nhỏ nhất của biểu thức ![]() bằng:
bằng:
Ta có:
(đúng do
)
Dấu bằng xảy ra khi và chỉ khi a = b hoặc ab = 1
Áp dụng bất đẳng thức trên ta có:
Đặt . Xét hàm số
trên đoạn [1; 3]
Do
Ta có bảng biến thiên
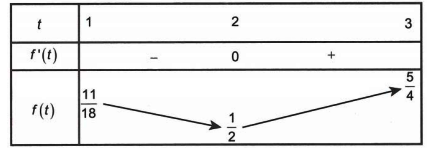
Suy ra khi và chỉ khi
Với a, b là các số thực dương tùy ý và a khác 1, đặt ![]() . Mệnh đề nào dưới đây đúng?
. Mệnh đề nào dưới đây đúng?
Ta có:
Tìm tập xác định của hàm số ![]()
Điều kiện xác định
=> Tập xác định của hàm số là
Hàm số nào sau đây đồng biến trên các khoảng (-∞; 2) và (2; +∞)?
Ta có:
Vậy hàm số đồng biến trên các khoảng (-∞; 2) và (2; +∞)
Cho hàm số y = f(x) có bảng biến thiên như sau:
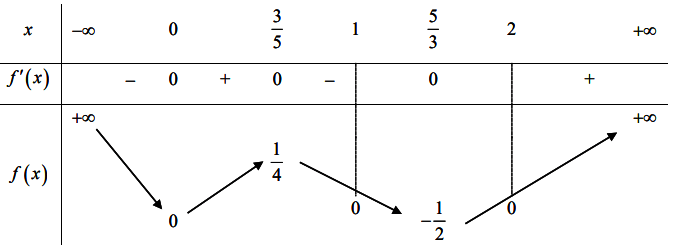
Hỏi đồ thị hàm số ![y = \frac{{{f^2}\left( x ight)\sqrt {{x^2} + x} }}{{\left[ {{f^2}\left( x ight) - 2f\left( x ight)} ight]\left( {2{x^5} + {x^4} - 10{x^3} - 5{x^2} + 8x + 4} ight)}}](https://i.khoahoc.vn/data/image/holder.png) có bao nhiêu tiệm cận đứng và tiệm cận ngang?
có bao nhiêu tiệm cận đứng và tiệm cận ngang?
Dựa vào bảng biến thiên ta có:
Ta có:
Dựa vào bảng biến thiên suy ra phương trình f(x) = 2 có 2 nghiệm x = a hoặc x = b trong đó a < 0, b > 2
Với điều kiện thì phương trình
Do đó đồ thị hàm số có 4 đường tiệm cận đứng
Mặt khác bậc của tử số nhỏ hơn bậc của mẫu số nên đồ thị hàm số có một tiệm cận ngang là y = 0 => Đồ thị hàm số có 5 đường tiệm cận.
Cho biết ![]() với
với ![]() . Chọn khẳng định đúng?
. Chọn khẳng định đúng?
Ta có:
Vậy
Tìm giá trị tham số ![]() để đồ thị hàm số
để đồ thị hàm số ![]() có ba điểm cực trị
có ba điểm cực trị ![]() sao cho trục
sao cho trục ![]() chia tam giác
chia tam giác ![]() thành một tam giác và một hình thang biết rằng tỉ lệ diện tích tam giác nhỏ được chia ra và diện tích hình thang bằng
thành một tam giác và một hình thang biết rằng tỉ lệ diện tích tam giác nhỏ được chia ra và diện tích hình thang bằng ![]() ?
?
Ta có:
Hàm số có ba điểm cực trị khi và chỉ khi có ba nghiệm phân biệt
Khi đồ thị hàm số có ba điểm cực trị là
,
,
Ta có: , B và C đối xứng với nhau qua
suy ra tam giác
cân tại
Hình vẽ minh họa
Trục hoành chia tam giác thành một tam giác và một hình thang
Kết hợp với điều kiện ta được
Khi đó gọi D; E lần lượt là giao điểm của Ox và các cạnh AB; AC. Gọi K là giao điểm của BC và Oy
Ta có:
Mà
Vì
.
Cho các số thực dương a, b với ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Trường hợp 1:
Trường hợp 2:
Vậy
Phương trình ![]() có tập nghiệm là:
có tập nghiệm là:
PT
.
Cho hàm số ![]() . Hàm số
. Hàm số ![]() có đồ thị như hình vẽ:
có đồ thị như hình vẽ:

Gọi ![]() là tập hợp tất cả các giá trị nguyên dương của tham số
là tập hợp tất cả các giá trị nguyên dương của tham số ![]() sao cho hàm số
sao cho hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() . Hỏi tập hợp
. Hỏi tập hợp ![]() có tất cả bao nhiêu phần tử?
có tất cả bao nhiêu phần tử?
Cho hàm số . Hàm số
có đồ thị như hình vẽ:
Gọi là tập hợp tất cả các giá trị nguyên dương của tham số
sao cho hàm số
đồng biến trên khoảng
. Hỏi tập hợp
có tất cả bao nhiêu phần tử?
Cho phương trình ![]() . Khẳng định nào sau đây là đúng?
. Khẳng định nào sau đây là đúng?
Ta có:
Đặt .
Khi đó
Với .
Cho hàm số ![]() có bảng xét dấu
có bảng xét dấu ![]() như sau:
như sau:

Hàm số ![]() đồng biến trong khoảng nào dưới đây?
đồng biến trong khoảng nào dưới đây?
Cho hàm số có bảng xét dấu
như sau:
Hàm số đồng biến trong khoảng nào dưới đây?
Một hình nón có đường cao bằng 9 cm nội tiếp trong một hình cầu bán kính bằng 5 cm. Tỉ số giữa thể tích khối nón và khối cầu là:
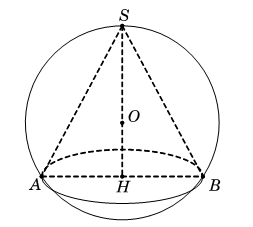
Hình vẽ kết hợp với giả thiết, ta có
Suy ra và
Thể tích khối nón (đvtt).
Thể tích khối cầu (đvtt).
Suy ra
Tâm tất cả các mặt của một hình lập phương là các đỉnh của hình nào trong các hình sau đây?
Tâm tất cả các mặt của một hình lập phương là các đỉnh của hình bát diện:

Cho hàm số ![]() . Tính tổng
. Tính tổng ![]() là:
là:
Với ta có:
Nhận thấy
Số đường tiệm cận của đồ thị hàm số ![]()
Quy đồng biến đổi hàm số đã cho trở thành
Tìm được tiệm cận đứng là x = -1 và x = 4 và không có tiệm cận ngang
=> Số tiệm cận là 2 đường
Tập nghiệm của bất phương trình ![]() là:
là:
Ta có:
.
Nghiệm nguyên lớn nhất của bất phương trình là:
x=7 || X=7 || x bằng 7 || 7
Nghiệm nguyên lớn nhất của bất phương trình là:
x=7 || X=7 || x bằng 7 || 7
Điều kiện:
Ta có:
.
Vậy nghiệm nguyên lớn nhất của bất phương trình là: .
Cho hàm số ![]() . Định
. Định ![]() để hàm số đạt cực đại tại
để hàm số đạt cực đại tại ![]() ?
?
Ta có:
Hàm số đạt cực đại tại điểm khi
Vậy đáp án cần tìm là .
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số nào dưới đây?
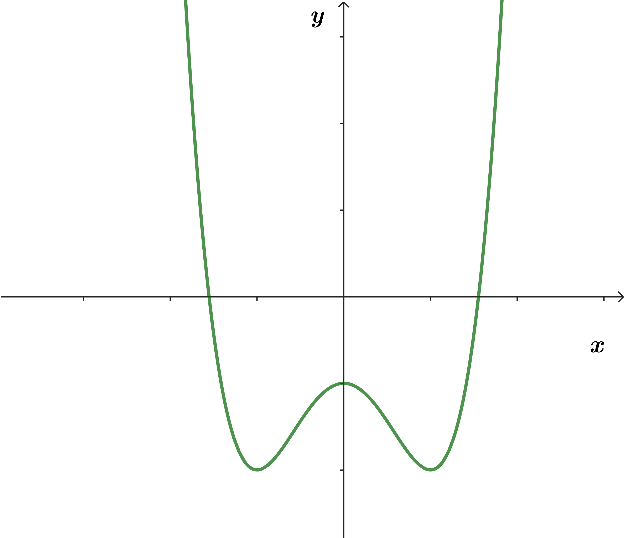 |
Dựa vào đồ thị hàm số ta thấy
=> Hệ số a > 0
=> Loại đáp án B và đáp án D
Mặt khác hàm số có ba điểm cực trị
=> Loại đáp án C
Chọn khẳng định đúng trong các khẳng định sau:
Tâm tất cả các mặt của một hình tứ diện đều là các đỉnh của một hình tứ diện đều:
Mặt cầu (S) có tâm A(1; -2; 2) và bán kính R = 8. Tìm phương trình mặt cầu (S).
Phương trình mặt cầu tâm bán kính R có dạng:
Có bao nhiêu giá trị nguyên của tham số ![]() để hàm số
để hàm số ![]() đồng biến trên từng khoảng xác định?
đồng biến trên từng khoảng xác định?
Có bao nhiêu giá trị nguyên của tham số để hàm số
đồng biến trên từng khoảng xác định?
Khối lăng trụ ngũ giác có bao nhiêu cạnh?
Khối lăng trụ ngũ giác có số cạnh của một mặt đáy là 5 cạnh, số cạnh bên là 5 cạnh
Số cạnh của khối lăng trụ ngũ giác là: 2.5 + 5 =15 cạnh.
Trong không gian với hệ tọa độ ![]() , cho điểm
, cho điểm ![]() . Mặt cầu
. Mặt cầu ![]() có tâm
có tâm ![]() và đi qua hai điểm
và đi qua hai điểm ![]() có phương trình là:
có phương trình là:
Ta có:
Vì đi qua hai điểm
nên
Vậy phương trình mặt cầu cần tìm là: .
Cho hàm số y = f(x) xác định, liên tục trên ![]() và có bảng biến thiên như sau:
và có bảng biến thiên như sau:
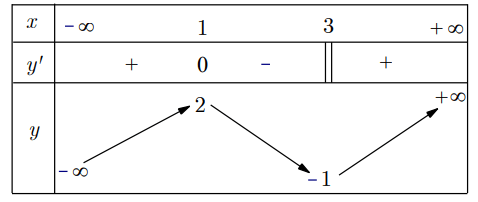
Khẳng định nào sau đây là đúng?
Từ bảng biến thiên, ta dễ dàng thấy được A, B, D sai, C đúng
Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng ![]() . Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng
. Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng ![]() . Khoảng cách giữa AB và trục của hình trụ bằng:
. Khoảng cách giữa AB và trục của hình trụ bằng:
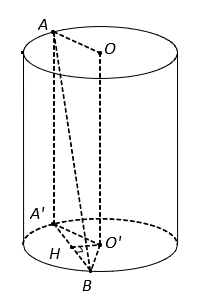
Từ hình vẽ kết hợp với giả thiết, ta có .
Gọi AA’ là đường sinh của hình trụ thì và
.
Vì nên
Gọi H là trung điểm A’B, suy ra
nên .
Tam giác ABA’ vuông tại A’ nên
Suy ra tam giác A’BO đều có cạnh bằng R nên
Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng ![]() . Diện tích xung quanh và diện tích toàn phần của hình lần lượt có giá trị là:
. Diện tích xung quanh và diện tích toàn phần của hình lần lượt có giá trị là:
Diện tích xung quanh của hình trụ: (đvdt).
Diện tích toàn phần của hình trụ:
(đvdt).
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:

Đồ thị hàm số trên có tiệm cận ngang là:
Dựa vào bảng biến thiên ta có:
Suy ra tiệm cận ngang của đồ thị hàm số là .
Trong không gian ![]() , cho điểm A(1;2;-1) và mặt phẳng
, cho điểm A(1;2;-1) và mặt phẳng ![]() . Xét các mặt cầu (S) có tâm
. Xét các mặt cầu (S) có tâm ![]() , đi qua điểm A, tiếp xúc với mặt phẳng (P) . Tính giá trị của biểu thức
, đi qua điểm A, tiếp xúc với mặt phẳng (P) . Tính giá trị của biểu thức ![]() khi (S) có bán kính nhỏ nhất.
khi (S) có bán kính nhỏ nhất.
Gọi H là hình chiếu của I trên mặt phẳng (P) ta có nên R nhỏ nhất khi
thẳng hàng và I là trung điểm của AH.
Phương trình AH đi qua A và vuông góc với mặt phẳng (P) có phương trình là
Tọa độ H là nghiệm của hệ:
Suy ra, ta có:
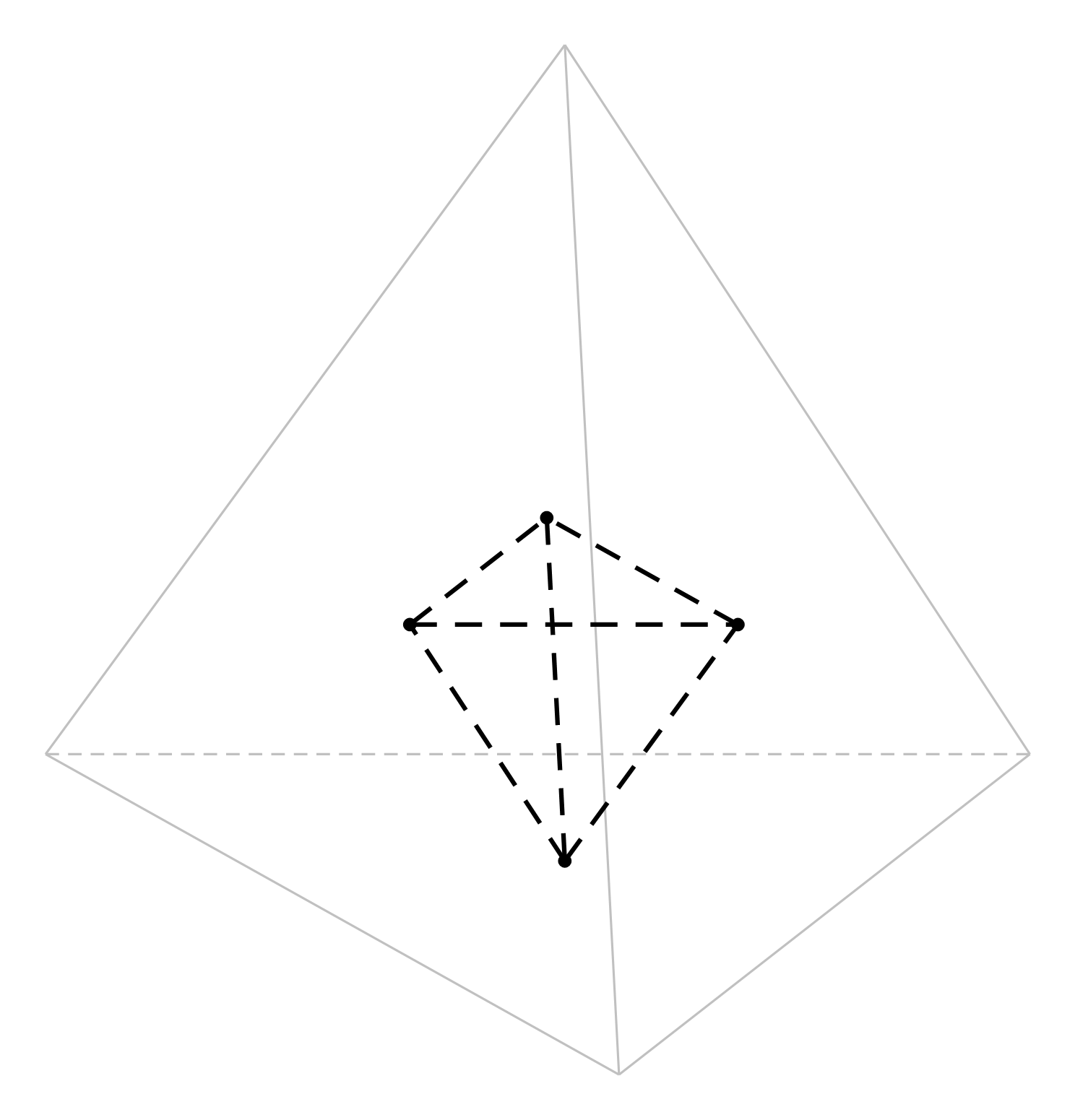
Cho khối đa diện đều loại ![]() . Tổng các góc phẳng tại một đỉnh của khối đa điện đó bằng?
. Tổng các góc phẳng tại một đỉnh của khối đa điện đó bằng?
Khối đa diện đều loại là khối bát diện đều.
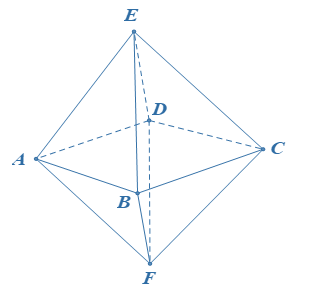
Mỗi đỉnh là đỉnh chung của 4 mặt.
Vậy tổng các góc phẳng tại một đỉnh của khối đa diện đó bằng .
Cho hình nón có bán kính đáy là ![]() , độ dài đường sinh là
, độ dài đường sinh là ![]() . Thể tích khối cầu nội tiếp hình nón bằng:
. Thể tích khối cầu nội tiếp hình nón bằng:
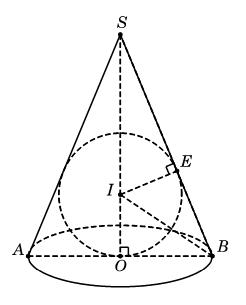
Xét mặt phẳng qua trục SO của hình nón ta được thiết diện là tam giác cân SAB.
Mặt phẳng đó cắt mặt cầu theo đường tròn có bán kính r (bán kính mặt cầu) và nội tiếp trong tam giác cân SAB.
Trong tam giác vuông SOB, gọi I là giao điểm của đường phân giác trong góc B với đường thẳng SO.
Chứng minh được I là tâm đường tròn nội tiếp tam giác và bán kính (E là hình chiếu vuông góc của I trên SB).
Theo tính chất phân giác, ta có .
Lại có .
Từ đó suy ra .
Ta có nên
Thể tích khối cầu: (đvtt).
Tổng các nghiệm của phương trình ![]() là:
là:
Điều kiện . Có
Dó đó, tổng các nghiệm sẽ bằng .
Tìm giá trị của tham số ![]() để giá trị nhỏ nhất của hàm số
để giá trị nhỏ nhất của hàm số ![]() trên đoạn
trên đoạn ![]() bằng
bằng ![]() ?
?
Ta có:
Vậy giá trị cần tìm là .
Cho hàm số ![]() có bảng biến thiên như hình vẽ dưới đây:
có bảng biến thiên như hình vẽ dưới đây:
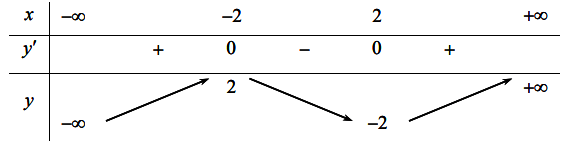
Số nghiệm của phương trình ![]() là:
là:
Ta có:
Khi đó suy ra phương trình (1) có 1 nghiệm; phương trình (2) có 3 nghiệm và phương trình (3) có 1 nghiệm.
=> Phương trình có 5 nghiệm
Giá trị của biểu thức ![]() là:
là:
Ta có:
Để chuẩn bị cho hoạt động cắm trại, bạn An tìm hiểu các mẫu lều cắm trại có kích thước như trong hình vẽ.
 Bạn An muốn biết thể tích chênh lệch của hai lều nên thực hiện tính
Bạn An muốn biết thể tích chênh lệch của hai lều nên thực hiện tính ![]() , trong đó
, trong đó ![]() lần lượt là thể tích của mẫu lều cắm trại ở hình a, hình b. Giá trị của
lần lượt là thể tích của mẫu lều cắm trại ở hình a, hình b. Giá trị của ![]() bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng đơn vị)?
bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng đơn vị)?
Đáp án: 961 dm3
Để chuẩn bị cho hoạt động cắm trại, bạn An tìm hiểu các mẫu lều cắm trại có kích thước như trong hình vẽ.
Bạn An muốn biết thể tích chênh lệch của hai lều nên thực hiện tính
, trong đó
lần lượt là thể tích của mẫu lều cắm trại ở hình a, hình b. Giá trị của
bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng đơn vị)?
Đáp án: 961 dm3
Cả hai lều đều có dạng khối lăng trụ đứng ngũ giác.
Xét khối lăng trụ ở hình a. Chia mặt đáy thành hai phần bao gồm: hình chữ nhật có chiều rộng , chiều dài
; tam giác cân có cạnh đáy dài
, chiều cao
như hình dưới đây.
Diện tích mặt đáy của lăng trụ đó là:
Vậy thể tích của khối lăng trụ ngũ giác đó là:
.
Xét khối lăng trụ ở hình . Chia mặt đáy thành hai phần bao gồm: hình thang cân có đáy lớn đài
, đáy nhỏ dài
, chiều cao
tam giác cân có cạnh đáy dài
, chiều cao
như hình vẽ .
Diện tích mặt đáy của lăng trụ đó là:
Vậy thể tích của khối lăng trụ ngũ giác đó là:
Do đó .
Cho hàm số ![]() có đồ thị hàm số như hình vẽ:
có đồ thị hàm số như hình vẽ:

Mệnh đề nào sau đây sai?
Giá trị cực đại của hàm số là suy ra mệnh đề sai là: “Giá trị cực đại của hàm số là
.”
Cho khối chóp ![]() có đáy
có đáy ![]() là hình vuông cạnh
là hình vuông cạnh ![]() , tam giác
, tam giác ![]() cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy,
cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy, ![]() . Tính theo
. Tính theo ![]() thể tích của khối chóp
thể tích của khối chóp ![]() .
.
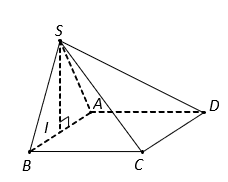
Gọi là trung điểm của
. Tam giác
cân tại
và có
là trung điểm
nên
. Do
theo giao tuyến
nên
.
Tam giác vuông , có:
Nếu đặt ![]() thì bất phương trình
thì bất phương trình ![]() trở thành bất phương trình nào?
trở thành bất phương trình nào?
Điều kiện:
Ta có:
Vậy thay , ta được
.
Tổng số cạnh của các loại hình {3;4} và {5;3} là bao nhiêu?
Hình {3;4} là khối bát diện đều, có 12 cạnh.
Hình {5;3} là khối mười hai mặt đều, có 30 cạnh.
Vậy tổng số cạnh của hai hình trên là cạnh.
Chọn hàm số tương ứng với bảng biến thiên sau?

Từ bảng biến thiên ta suy ra đồ thị hàm số bậc 4 trùng phương có hệ số nên hàm số cần tìm là
.
Để đồ thị hàm số ![]() có ba điểm cực trị tạo thành một tam giác có diện tích bằng
có ba điểm cực trị tạo thành một tam giác có diện tích bằng ![]() . Tìm giá trị tham số
. Tìm giá trị tham số ![]() thỏa mãn yêu cầu bài toán?
thỏa mãn yêu cầu bài toán?
Để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác có diện tích bằng
. Tìm giá trị tham số
thỏa mãn yêu cầu bài toán?
Cho hàm số ![]() . Xét tính đúng sai của các khẳng định sau:
. Xét tính đúng sai của các khẳng định sau:
a) Tập xác định của hàm số là ![]() . Sai||Đúng
. Sai||Đúng
b) Đạo hàm của hàm số là ![]() . Đúng||Sai
. Đúng||Sai
c) Giá trị lớn nhất của hàm số trên ![]() là 2. Sai||Đúng
là 2. Sai||Đúng
d) Giá trị nhỏ nhất của hàm số trên ![]() là
là ![]() . Đúng||Sai
. Đúng||Sai
Cho hàm số . Xét tính đúng sai của các khẳng định sau:
a) Tập xác định của hàm số là . Sai||Đúng
b) Đạo hàm của hàm số là . Đúng||Sai
c) Giá trị lớn nhất của hàm số trên là 2. Sai||Đúng
d) Giá trị nhỏ nhất của hàm số trên là
. Đúng||Sai
Tập xác định của hàm số là .
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
Ta có:
Khi đó
Ta có:
Anh T đã làm hợp đồng xin vay vốn ngân hàng để kinh doanh với số tiền 200 triệu đồng với lãi suất a% trên một năm. Điều kiện hợp đồng là số tiền lại tháng trước sẽ được tính làm vốn để sinh lãi cho tháng sau. Sau hai năm kinh doanh, anh T dã thanh toán hợp đồng ngân hàng với số tiền làm tròn là 245512000 đồng. Chọn khẳng định đúng?
Lãi suất mỗi tháng là . Theo công thức lãi kép ta có:
Cho hàm số ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Hàm số có các tính chất như sau:
Đồ thị hàm số nhận trục tung làm tiệm cận đứng
Đồ thị hàm số nhận trục hoành làm tiệm cận ngang
Là hàm số nghịch biến trên
Hằng ngày mực nước của hồ thủy điện ở miền Trung lên và xuống theo lượng nước mưa, và các suối nước đổ về hồ. Từ lúc 8h sáng, độ sâu của mực nước trong hồ tính theo mét và lên xuống theo thời gian t (giờ) trong ngày cho bởi công thức ![]() . Biết rằng phải thông báo cho các hộ dân di dời trước khi xả nước theo quy định trước 5 tiếng. Hỏi cần thông báo cho hộ dân di dời trước khi xả nước lúc mấy giờ. Biết rằng mực nước trong hồ phải lên cao nhất mới xả nước.
. Biết rằng phải thông báo cho các hộ dân di dời trước khi xả nước theo quy định trước 5 tiếng. Hỏi cần thông báo cho hộ dân di dời trước khi xả nước lúc mấy giờ. Biết rằng mực nước trong hồ phải lên cao nhất mới xả nước.
Đáp án: 15
Hằng ngày mực nước của hồ thủy điện ở miền Trung lên và xuống theo lượng nước mưa, và các suối nước đổ về hồ. Từ lúc 8h sáng, độ sâu của mực nước trong hồ tính theo mét và lên xuống theo thời gian t (giờ) trong ngày cho bởi công thức . Biết rằng phải thông báo cho các hộ dân di dời trước khi xả nước theo quy định trước 5 tiếng. Hỏi cần thông báo cho hộ dân di dời trước khi xả nước lúc mấy giờ. Biết rằng mực nước trong hồ phải lên cao nhất mới xả nước.
Đáp án: 15
Ta có:
Bảng biến thiên:
Mực nước lên cao nhất thì phải mất giờ.
Hay mực nước lên cao nhất là lúc 20 giờ.
Vậy phải thông báo cho dân di dời vào giờ chiều cùng ngày.
