Góc ở tâm. Số đo cung Toán 9

Chuyên đề Góc với đường tròn gồm nội dung trọng tâm giúp bạn học ôn tập, củng cố lại kiến thức Toán 9 ôn thi vào lớp 10.

Khoahoc Góc ở tâm. Số đo cung Toán 9 5,0

I. KIẾN THỨC CẦN NHỚ

1. Góc ở tâm

Định nghĩa

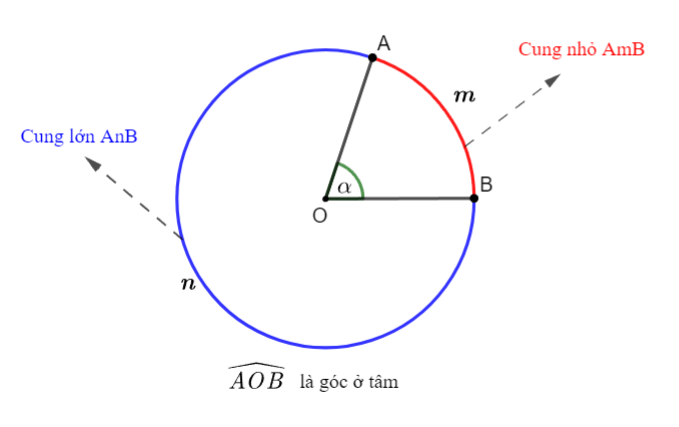
- Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.

Nếu $0^{0} < \alpha < 180^{0}$ thì cung nằm bên trong góc gọi là cung nhỉ, cung nằm bên ngoài góc gọi là cung lớn.
Nếu $\alpha = 180^{0}$ thì mỗi cung là một nửa đường tròn.
Cung nằm bên trong góc được gọi là cung bị chắn.
Góc bẹt chắn nửa đường tròn.
Kí hiệu cung $AB$ là: $\widehat{AB}$ .

2. Số đo cung

Số đo của cung $AB$ được kí hiệu là $sd\widehat{AB}$ .
Số đo của cung nhỏ bằng số đo góc ở tâm chắn cung đó.
Số đo của cung lớn bằng hiệu giữa $360^{0}$ và số đo của cung nhỏ (có chung hai mút với cung lớn).
Số đo của nửa đường tròn bằng $180^{0}$ . Cung cả đường tròn có số đo bằng $360^{0}$ . Cung không có số đo $0^{0}$ (cung có hai mút trùng nhau).

3. So sánh hai cung

Trong một đường tròn hay hai đường tròn bằng nhau:

Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.
Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

Định lí: Nếu C là một điểm nằm trên cung AB thì:

$sd\widehat{AB} = sd\widehat{AC} + sd\widehat{CB}$

Dạng 1: Tính số đo góc ở tâm và số đo của cung bị chắn.

Phương pháp giải

Để tính số đo của góc ở tâm, số đo của cung bị chắn ta sử dụng các kiến thức sau:

Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.Số đo của cung lớn bằng hiệu giữa $360^{0}$ và số đo cung nhỏ (có chung hai mút với cung lớn).

Số đo của nửa đường tròn bằng $180^{0}$ . Cung cả đường tròn có số đo $360^{0}$ .

Sử dụng tỉ số lượng giác của một góc nhọn để tính góc. Sử dụng quan hệ đường kính và dây cung.

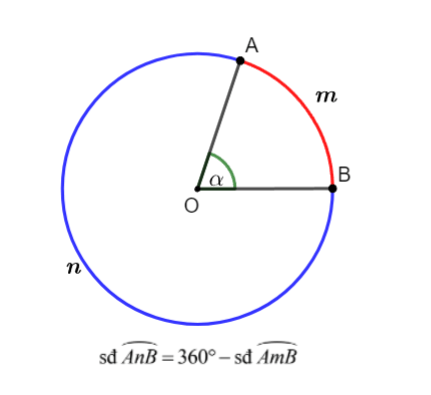Chú ý: Khi nhắc tới một cung là nhắc tới cung nhỏ.

Ví dụ: Cho đường tròn $(O;R)$ và dây cung $MN = R\sqrt{3}$ . Tính số đo của hai cung $MN$ .

Hướng dẫn giải

Hình vẽ minh họa

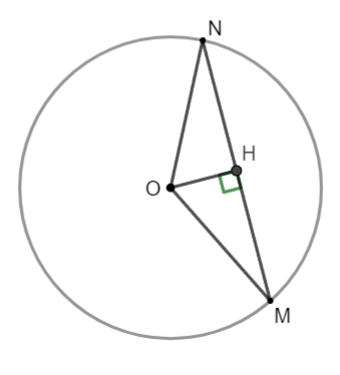
Góc ở tâm. Số đo cung Toán 9

Kẻ $OH\bot MN \equiv H$

$\Rightarrow HM = HN$ (định lí về đường kính vuông góc với dây cung)

Do đó $HM = HN = \frac{MN}{2} = \frac{R\sqrt{3}}{2}$

Ta có: $\cos\widehat{HMO} = \dfrac{HM}{MO}= \dfrac{\dfrac{R\sqrt{3}}{2}}{R} = \dfrac{\sqrt{3}}{2}$

$\Rightarrow \widehat{HMO} = 30^{0} \Rightarrow \widehat{MON} = 120^{0}$

Suy ra số đo cung nhỏ $MN$ bằng $\widehat{MON} = 120^{0}$

số đo cung lớn $MN$ bằng $360^{0} - 120^{0} = 240^{0}$

Ví dụ: Cho đường tròn $(O)$ dây cung $AB$ . Tiếp tuyến của $(O)$ tại $AB$ cắt nhau tại $M$ . Biết rằng $\widehat{AMB} = 50^{0}$ .

a) Tính số đo cung $AB$ .

b) Trên nửa mặt phẳng bờ $OB$ (không chứa điểm $A$ ), kẻ đường thẳng $d$ qua $O$ và song song với $BM$ , $d$ cắt $(O)$ tại $D$ . Tính số đo cung $AD$ .

Hướng dẫn giải

Hình vẽ minh họa

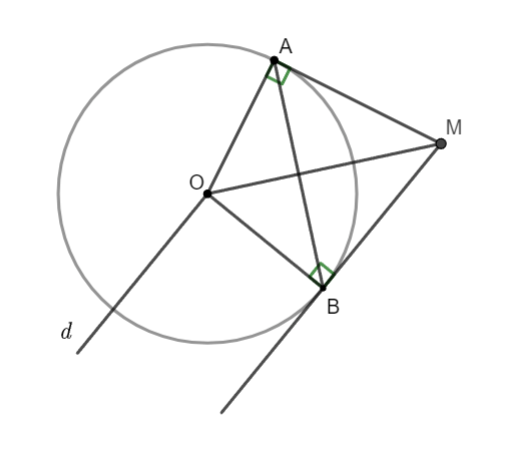
Góc ở tâm. Số đo cung Toán 9

Vì $MA;MB$ là hai tiếp tuyến của đường tròn $(O)$ nên $MA\bot OA;MB\bot OB$

Xét tứ giác $AOBM$ có:

$\widehat{AOB} = 360^{0} - \left( \widehat{MAO} + \widehat{MBO} + \widehat{AMB} \right)$

$= 360^{0} - \left( 90^{0} + 90^{0} + 50^{0} \right) = 130^{0}$

$sd\widehat{AB} = \widehat{AOB} = 130^{0}$

b) Ta có: $sd\widehat{ADB} = 360^{0} - sd\widehat{AB} = 360^{0} - 130^{0} = 230^{0}$

Mặt khác $OD//BM$ mà $BM\bot OB \Rightarrow OD\bot OB$ hay $sd\widehat{BOD} = 90^{0}$

$\Rightarrow sd\widehat{BOD} = sd\widehat{ADB} - sd\widehat{BD} = 230^{0} - 90^{0} = 140^{0}$

Ví dụ: Cho tam giác đều $ABC$ . Vẽ đường tròn $(I)$ đường kính $BC$ cắt các cạnh $AB;AC$ lần lượt tại $D;E$ .

a) Tính số đo mỗi cung $BD$ (cung lớn và cung nhỏ).

b) Chứng minh rằng: $\widehat{BD} = \widehat{DE} = \widehat{EC}$

Hướng dẫn giải

Hình vẽ minh họa

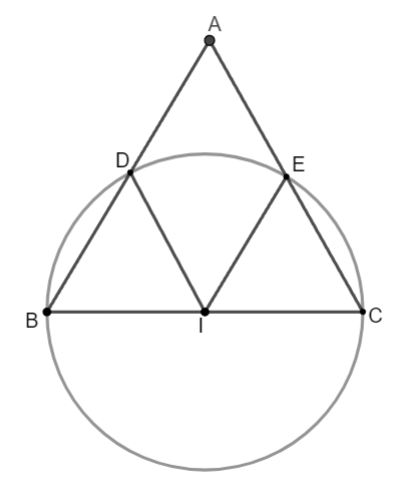
Góc ở tâm. Số đo cung Toán 9

a) Ta có: $IB = ID( = R)$ suy ra tam giác $IBD$ cân tại $I$ .

Mà $\widehat{DBI} = 60^{0}$ (tam giác $ABC$ đều)

Do đó $\Delta IBD$ đều.

Suy ra $\widehat{BID} = 60^{0} \Rightarrow sd\widehat{BD} = 60^{0}$

Vậy $sd\widehat{BD}$ lớn $= 360^{0} - 60^{0} = 300^{0}$

b) Ta có: $sd\widehat{BD} = 60^{0}$

Tương tự ta cũng có $sd\widehat{EC} = 60^{0}$

Suy ra $sd\widehat{DE} = sd\widehat{BC} - sd\widehat{BD} - sd\widehat{EC} = 60^{0}$

Ta có:

$sd\widehat{BD} = sd\widehat{DE} = sd\widehat{EC}$ nên $\widehat{BD} = \widehat{DE} = \widehat{EC}$ .

Ví dụ: Cho đường tròn $(O;R)$ , lấy $B \in (O)$ . Gọi $H$ là trung điểm đoạn $OB$ . Dây $CD$ vuông góc với $OB$ tại $H$ . Tính số đo cung nhỏ và cung lớn $CD$ .

Hướng dẫn giải

Hình vẽ minh họa

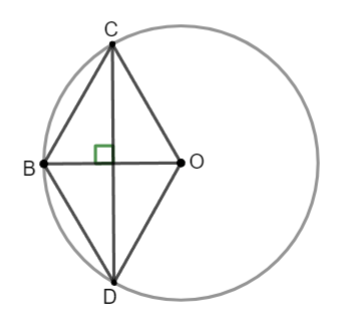
Góc ở tâm. Số đo cung Toán 9

Ta có: $OB = OC( = R)$ suy ra $\Delta BOC$ cân tại $O$ .

Lại có: $BO\bot CD$ tại trung điểm của $OB$ .

Suy ra $\Delta BOC$ cân tại $C$

Do đó $\Delta BOC$ đều.

Chứng minh tương tự ta được: $\Delta BOD$ đều.

Suy ra $sd\widehat{CBD} = \widehat{COD} = \widehat{COB} + \widehat{BOD} = 120^{0}$

Suy ra $sd\widehat{CD} = 360^{0} - 120^{0} = 240^{0}$

Dạng 2: Chứng minh hai cung bằng nhau

Phương pháp giải

Sử dụng các định lí, hệ quả và ứng dụng kiến thức đã học vào để chứng minh hai góc ở tâm bằng nhau hoặc hau dây bằng nhau suy ra hai cung bằng nhau.

Ví dụ: Cho tam giác $ABC$ đều. Trên nửa mặt phẳng bờ $BC$ không chứa $A$ , vẽ nửa đường tròn đường kính $BC$ . Lấy điểm $D$ thuộc nửa đường tròn sao cho $sd\widehat{CD} = 60^{0}$ . Gọi $I$ là giao điểm của $AD$ và $BC$ . Chứng minh rằng $BI = 2CI$ .

Hướng dẫn giải

Hình vẽ minh họa

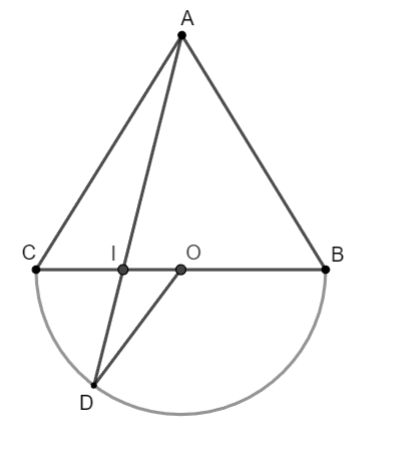
Góc ở tâm. Số đo cung Toán 9

Gọi $O$ là tâm của nửa đường tròn đường kính $BC$ .

Ta có: $sd\widehat{CD} = 60^{0}$ nên $\Delta OCD$ đều

$\Rightarrow \widehat{OCD} = \widehat{ABC} = 60^{0}$

Do đó: $\Delta AIB\sim\Delta DIC(g - g)$

$\Rightarrow \frac{BI}{CI} = \frac{AB}{CD}$ mà $AB = BC;CD = OC( = R)$

$\Rightarrow \frac{BI}{CI} = \frac{BC}{OC} = 2 \Rightarrow BI = 2CI$

Ví dụ: Cho hai đường tròn $(O;R)$ và $(O';R')$ cắt nhau tại hai điểm $A$ và $B$ . Kẻ các đường kính $AOC;AO'D$ . Hãy so sánh số đo (độ) của hai cung nhỏ $BC$ và $BD$ của hai đường tròn, biết rằng $R > R'$ .

Hướng dẫn giải

Hình vẽ minh họa

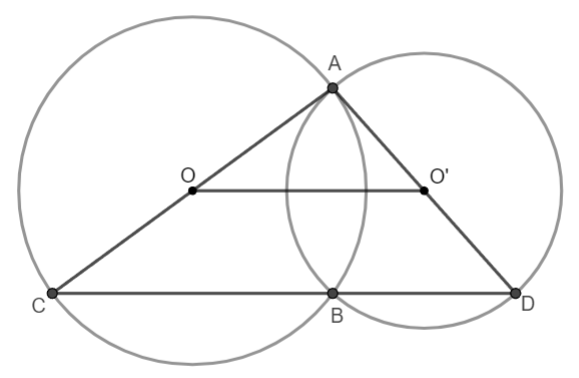
Góc ở tâm. Số đo cung Toán 9

Ta có: $R > R'$ (giả thiết) nên $OA > OA'$

Xét tam giác $AOO'$ ta có: $OA > OA'$ nên $\widehat{AOO'} > \widehat{AO'O}$

$\Rightarrow 2\widehat{AOO'} > 2\widehat{AO'O} \Rightarrow \widehat{AOB} < \widehat{AO'B}$

$\Rightarrow \widehat{BOC} < \widehat{BO'D}$ (hai góc kề bù với hai góc trên)

Vậy số đo (độ) của cung nhỏ $BC$ lớn hơn số đo (độ) của cung nhỏ $BD$ .

Ví dụ: Trên cung nhỏ $AB$ của $(O)$ , cho hai điểm $C$ và $D$ sao cho cung $AB$ được chia thành ba cung bằng nhau $\widehat{AC} = \widehat{CD} = \widehat{BD}$ . Bán kính $OC$ và $OD$ cắt dây $AB$ lần lượt tại $E$ và $F$ .

a) Hãy so sánh các đoạn thẳng $AE;FB$ .

b) Chứng minh các đường thẳng $AB$ và $CD$ song song.

Hướng dẫn giải

Hình vẽ minh họa

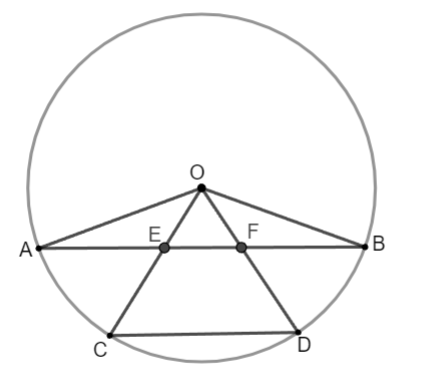
Góc ở tâm. Số đo cung Toán 9

a) Xét tam giác $OFB$ và $OEA$ ta có:

$OA = OB = R$

$\widehat{AOC} = \widehat{DOB}$ (do $\widehat{AC} = \widehat{BD}$ )

$\widehat{OAB} = \widehat{OBA}$ (tam giác $OAB$ cân tại $O$ do $OA = OB = R$ )

Do đó $\Delta OEA = \Delta OFB(g - c - g)$

$\Rightarrow AE = FB$

b) Do $\Delta OEA = \Delta OFB \Rightarrow OE = OF$ suy ra $\Delta OEF$ cân tại $O$ .

Suy ra $2\widehat{OEF} = 180^{0} - \widehat{EOF}$ (định lí tổng ba góc trong tam giác)

Chứng minh tương tự $\Delta OCD$ cân tại $O$ nên $2\widehat{OCD} = 180^{0} - \widehat{COD}$ (định lí tổng ba góc trong tam giác)

Do đó: $\widehat{OEF} = \widehat{OCD}$ mà hai góc này ở vị trí đồng vị.

Vậy $AB//CD$ (cặp góc đồng vị bằng nhau).

Ví dụ: Cho hai đường tròn bằng nhau $(O)$ và $(O')$ cắt nhau tại $A$ và $B$ . Kẻ dây $AM$ của đường tròn $(O)$ và dây $BN$ của đường tròn $(O')$ sao cho $AM//BN$ . Chứng minh $\widehat{AM} = \widehat{BN}$ .

Hướng dẫn giải

Hình vẽ minh họa

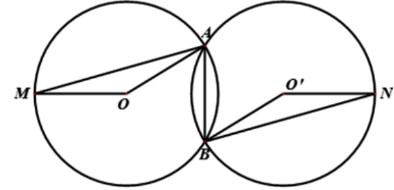
Góc ở tâm. Số đo cung Toán 9

Vì $AM//BN$ nên $\widehat{MAB} = \widehat{ABN}$ (so le trong) (1)

Mặt khác $OA = OB = O'A = O'B$

Suy ra tứ giác $OAO'B$ là hình thoi

$\Leftrightarrow \widehat{OAB} = \widehat{ABO'}$ (2)

Từ (1) và (2) suy ra $\widehat{MAO} = \widehat{NBO'}$

Ta có: $\Delta MOA$ cân tại $O$ và $\Delta NO'B$ cân tại $O'$ có góc ở đáy bằng nhau

$\Rightarrow \widehat{MOA} = \widehat{NO'B}$

Do đó $\Delta MOA = \Delta NO'B(c - g - c)$

$\Rightarrow AM = BN$

Mặt khác hai đường tròn $(O)$ và $(O')$ bằng nhau nên $\widehat{AM} = \widehat{BN}$ .

II. BÀI TẬP TỰ RÈN LUYỆN

Bài 1: Cho đường tròn $(O;R)$ và điểm $M$ nằm ngoài đường tròn đó. Gọi $MA;MB$ là hai tiếp tuyến với đường tròn tại $A$ và $B$ . Tính số đo góc ở tâm tạo bởi hai bán kính $OA;Ob$ nếu:

a) $\widehat{AMB} = 70^{0}$

b) $MA = R$

c) $MO = 2R$

Bài 2: Cho tam giác $ABC$ cân tại $A$ . Vẽ $(O)$ , đường kính $BC$ . Đường tròn $(O)$ cắt lần lượt tại $M;N$ .

a) Chứng minh các cung nhỏ $BM$ và $CN$ có số đo bằng nhau.

b) Tính $\widehat{MON}$ , biết $\widehat{BAC} = 40^{0}$ .

Bài 3: Trên một đường tròn $(O)$ có $sd\widehat{MP} = 100^{0}$ . Gọi $N;Q$ lần lượt là điểm đối xứng của $M;P$ qua $O$ . Trên cung $PQ$ lấy $C$ làm điểm chính giữa, trên cung $MN$ lấy $D$ làm điểm chính giữa. Tính số đo cung nhỏ $CD$ .

Bài 4: Cho đường tròn $(O;R)$ , lấy điểm $M$ nằm ngoài $(O)$ sao cho $OM = 2R$ . Từ $M$ kẻ tiếp tuyến $MA$ và $MB$ với $(O)$ (với $A;B$ các tiếp điểm).

a) Tính $\widehat{AOM}$ .

b) Tính $\widehat{AOB}$ và số đo cung $AB$ nhỏ.

c) Biết $OM$ cắt $(O)$ tại $C$ . Chứng minh $C$ là điểm chính giữa của cung nhỏ.

Bài 5: Cho hai tiếp tuyến tại $A;B$ của đường tròn $(O)$ cắt nhau tại $K$ , biết $\widehat{AKB} = 50^{0}$ và $KO$ cắt $(O)$ tại $M$ .

a) Tính $\widehat{AOM};\widehat{BOM}$ .

b) Số đo cung nhỏ $\widehat{AB}$ bằng bao nhiêu?

Bài 6: Cho đường tròn $(O)$ đường kính $AB$ , vẽ góc ở tâm $\widehat{AOC} = 50^{0}$ . Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$ . Chứng minh ba điểm $COE$ thẳng hàng. Từ đó tính số đo cung nhỏ $BE$ .

Bài 7: Cho đường tròn $(O;R)$ và một điểm $A$ nằm ngoài đường tròn sao cho $OA = 2R$ . Từ điểm $A$ vẽ hai tiếp tuyến $AB;AC$ tới đường tròn (với $B;C$ là các tiếp điểm). Tìm số đo cung lớn $\widehat{BC}$ của đường tròn.

Bài 8: Cho đường tròn đường kính $AB$ và dây $AC$ . Chứng minh rằng $\widehat{BAC} = \frac{1}{2}sd\widehat{BC}$ .

Bài 9: Cho tam giác $ABC$ có $\widehat{B} = 70^{0};\widehat{C} = 50^{0}$ . Đường tròn $(O)$ nội tiếp tam giác đó tiếp xúc với các cạnh $AB;BC;CA$ theo thứ tự tại $D;E;F$ . Tính số đo cung $\widehat{DE};\widehat{EF};\widehat{FD}.$

Bài 10: Cho nửa đường tròn $(O)$ đường kính $20cm$ , điểm $C$ là điểm chính giữa của nửa đường tròn. Lấy điểm $H$ thuộc $OA$ sao cho $OH = 6cm$ . Đường vuông góc với $OA$ tại $H$ cắt nửa đường tròn tại $D$ . Vẽ dây $AE$ song song với $AD$ . Gọi $K$ là hình chiếu của $E$ trên $AB$ . Tính diện tích tam giác $AEK$ .