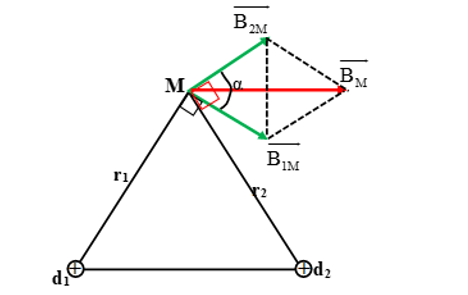
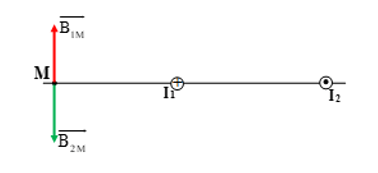
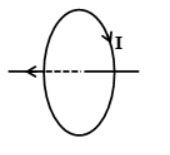
Trong một từ trường đều có phương ngang, cảm ứng từ có độ lớn 0,75T, người ta treo một đoạn dây dẫn mang dòng điện bằng hai sợi dây nhẹ, không co dãn, dài bằng nhau (hình vẽ).

Khi đoạn dây nằm cân bằng thì mặt phẳng chứa đoạn dây và hai dây treo có phương thẳng đứng. Cho biết đoạn dây mang dòng điện dài 20cm và có khối lượng không đáng kể. Cường độ dòng điện trong đoạn dây là 8A. Lực căng trên mỗi sợi dây treo có độ lớn là:
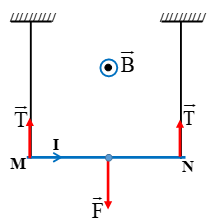
MN có khối lượng không đáng kể nên chịu tác dụng của , chiều lực từ được xác định như hình vẽ:
Lực từ có độ lớn:
Điều kiện cân bằng: