Cho hình vẽ dưới đây:
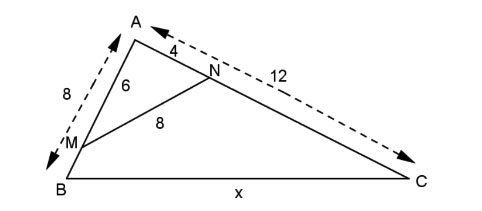
Tìm giá trị của x.
Ta có:
Xét tam giác ANM và tam giác ABC có:
Góc A chung
Khoahoc.vn xin gửi tới bạn đọc bài viết Bài tập Toán lớp 8: Các trường hợp đồng dạng của hai tam giác sách Chân trời sáng tạo. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé!
Cho hình vẽ dưới đây:

Tìm giá trị của x.
Ta có:
Xét tam giác ANM và tam giác ABC có:
Góc A chung
Cho tam giác ABC có ![]() , kẻ đường cao AH. Biết
, kẻ đường cao AH. Biết ![]()
![]() . Hệ thức nào sau đây đúng?
. Hệ thức nào sau đây đúng?
Xét tam giác ABC và tam giác HAC có:
Cho tam giác DEF và tam giác ILK, biết ![]()
![]() . Cần thêm điều kiện gì để
. Cần thêm điều kiện gì để ![]() ?
?
Ta có:
Để thì
(hai góc tạo bởi các cặp cạnh tỉ lệ).
Cho hình vẽ sau:
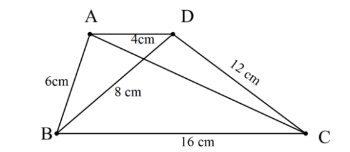
Hãy cho biết hai tam giác nào đồng dạng?
Ta có:
Cho hình thang ![]() ,
, ![]() . Độ dài đoạn thẳng CD là:
. Độ dài đoạn thẳng CD là:
Hình vẽ minh họa
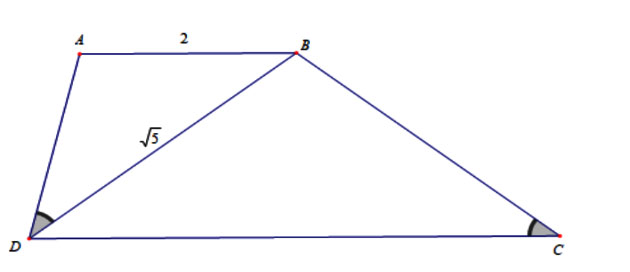
Ta có
Xét tam giác ADB và tam giác BCD ta có:
Cho hình thang ABCD có ![]() như hình vẽ:
như hình vẽ:
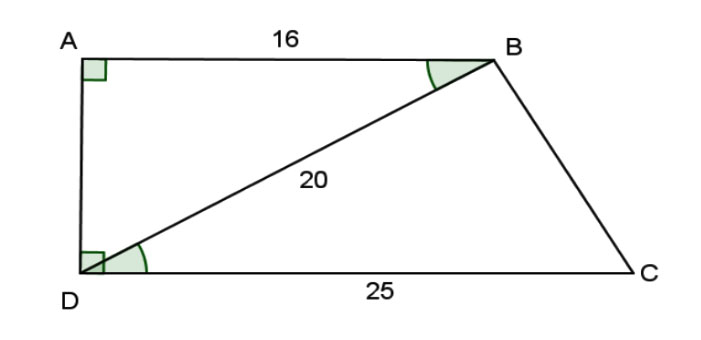
Độ dài cạnh BC là 15cm
Cho hình thang ABCD có như hình vẽ:

Độ dài cạnh BC là 15cm
Xét tam giác ABD và tam giác BDC có:
Ta có: nên
Theo định lí Pythagore ta có:
Cho tam giác ABC, lấy hai điểm D cạnh AB. Qua D kẻ đường thẳng song song với BC cắt AC tại E. Kết luận nào sau đây sai?
Hình vẽ minh họa
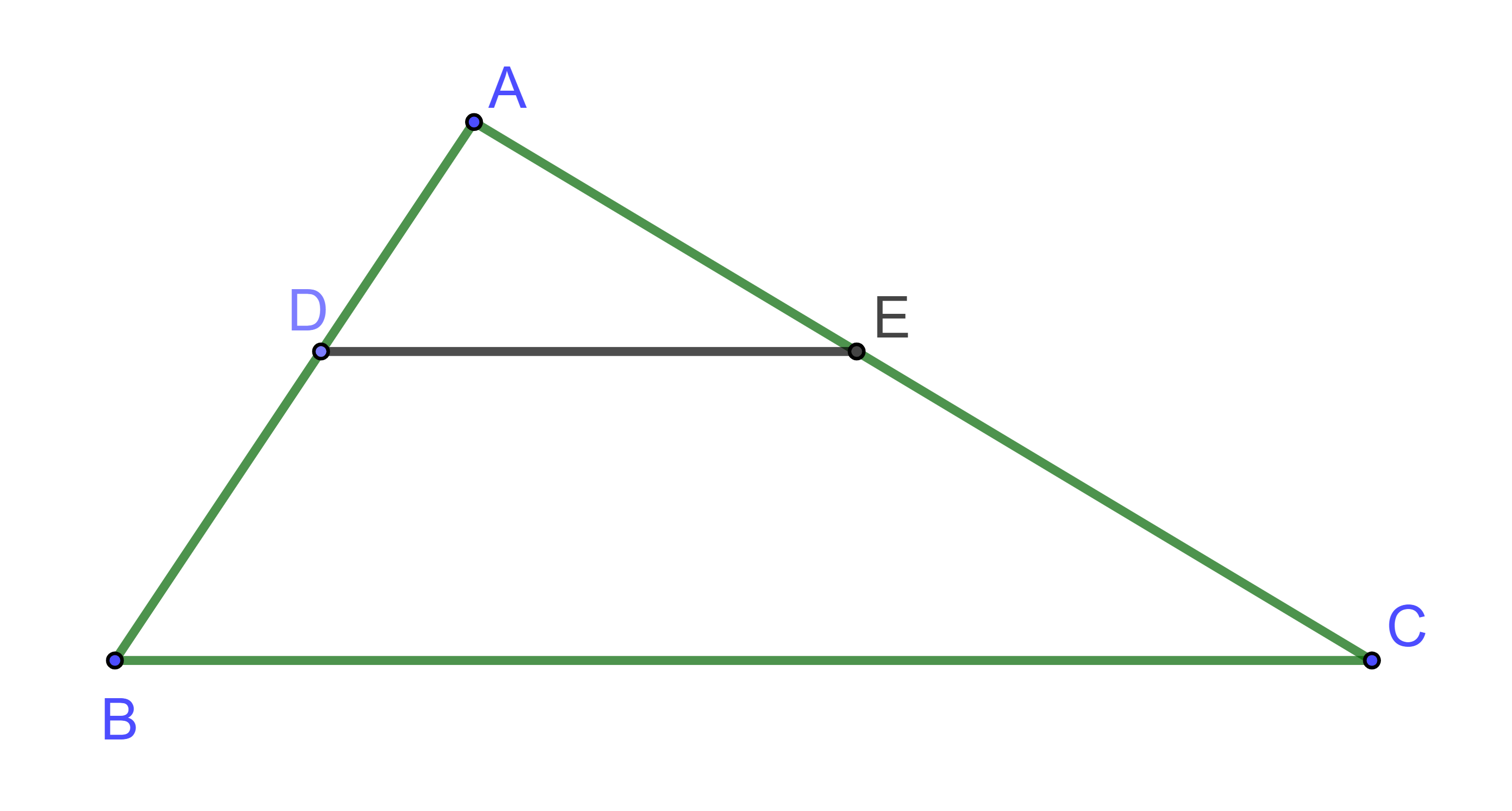
Vì DE // BC nên theo định lí Thales đảo ta có:
Xét tam giác ADE và tam giác ABC có
Góc A chung
Trong các cặp tam giác sau dây, cặp tam giác nào đồng dạng với nhau nếu các cạnh của hai tam giác là:
Vì nên hai tam giác có độ dài cạnh là: 1,5cm, 3cm, 4cm và 6cm, 12cm, 16cm đồng dạng với nhau.
Vì nên hai tam giác có độ dài cạnh là: 4cm, 5cm, 3cm và 8cm, 10cm, 7cm không đồng dạng với nhau.
Vì nên hai tam giác có độ dài cạnh là: 6dm, 5dm, 4dm và 18dm, 7dm, 6dm không đồng dạng với nhau.
Vì nên hai tam giác có độ dài cạnh là: 5cm, 7cm, 3cm và 10cm, 14cm, 8cm không đồng dạng với nhau.
Cho hình vẽ:
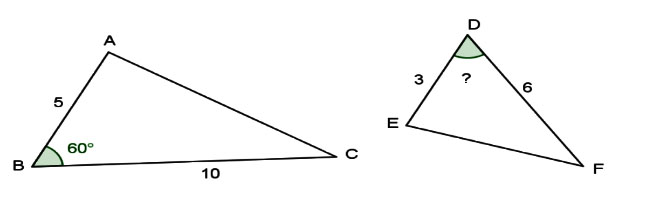
Để hai tam giác ABC và DEF đồng dạng với nhau thì số đo góc D trong hình vẽ bằng bao nhiêu?
Ta có:
Để hai tam giác đã cho đồng dạng thì (Hai góc tương ứng)
Cho ![]() biết
biết ![]() . Khi đó:
. Khi đó:
Vì nên
Cho tam giác ![]() có
có ![]() đồng dạng với tam giác
đồng dạng với tam giác ![]() có
có ![]() . Tìm tỉ số chu vi của hai tam giác MNP và ABC.
. Tìm tỉ số chu vi của hai tam giác MNP và ABC.
Ta có:
Lại có:
Vậy tỉ số chu vi tam giác MNP và chu vi tam giác ABC là
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Tính độ dài AH biết ![]()
Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta có:
Xét tam giác ABC và tam giác HBA có:
Góc B chung
Giả sử hai tam giác DEF và tam giác SRK có ![]() thì hệ thức nào sau đây đúng?
thì hệ thức nào sau đây đúng?
Xét tam giác DEF có:
Xét tam giác DEF và tam giác SRK có:
Nếu tam giác ABC và tam giác DEF có ![]() thì:
thì:
Xét tam giác ABC có:
(Tổng ba góc của một tam giác)
Xét tam giác ABC và tam giác FED có:
Hai tam giác nào dưới đây không đồng dạng với nhau?
Vì nên hai tam giác có độ dài cạnh là 4dm, 3dm, 2dm và 8dm, 6dm, 4dm đồng dạng với nhau.
Vì nên hai tam giác có độ dài cạnh là 40cm, 50cm, 60cm và 80cm, 100cm, 120cm đồng dạng với nhau.
Vì nên hai tam giác có độ dài cạnh là 14cm, 10cm, 14cm và 7cm, 7cm, 5cm đồng dạng với nhau.
Vì nên hai tam giác có độ dài cạnh là 9cm, 7cm, 3cm và 7cm, 14cm, 18cm không đồng dạng với nhau.
