Trong các khẳng định sau, khẳng định nào đúng?
Hình vuông là đa giác đều (vì các cạnh và các góc bằng nhau).
Mỗi góc của lục giác đều bằng:
Mỗi góc của đa giác đều n cạnh bằng
Mỗi góc của lục giác đều 6 cạnh bằng
Tổng số đo các góc trong đa giác n cạnh là:
Đa giác lồi n cạnh có số đường chéo xuất phát từ một đỉnh là n – 3 đường
Số tam giác không có điểm chung của n giác là : n – 2 tam giác
Tổng các góc trong n giác lồi bằng tổng các góc của n – 2 tam giác
Vậy tổng các góc trong của n giác lồi có số đo bằng
Cho phép quay tâm O (O là một điểm bất kì) với góc quay bằng bao nhiêu biến 
thành chính nó?
Vì phép quay và phép quay
giữ nguyên mọi điểm nên đáp án cần tìm là:
.
Cho bát giác đều ABCDEFGH nội tiếp đường tròn tâm O. Phép quay thuận chiều 1350 biến hình tam giác OAB thành tam giác nào?
Ta có: bát giác đều ABCDEFGH nội tiếp đường tròn tâm O nên AB = BC = CD = DE = EF = FG = GH = HA
Suy ra số đo các cung nhỏ AB; BC; CD; DE; EF; FG; GH; HA đều bằng 450.
Do đó phép quay thuận chiều 1350 biến điểm A thành điểm F, điểm B thành điểm G, điểm O thành điểm O.
=> Phép quay thuận chiều 1350 biến hình tam giác OAB thành tam giác OFG.
Mỗi góc trong một đa giác đều cạnh có số đo là:
Đa giác lồi n cạnh có số đường chéo xuất phát từ một đỉnh là n – 3 đường
Số tam giác không có điểm chung của n giác là : n – 2 tam giác
Tổng các góc trong n giác lồi bằng tổng các góc của n – 2 tam giác
Vậy tổng các góc trong của n giác lồi có số đo bằng
Hình n giác đều có n góc bằng nhau nên mỗi góc có số đo là .
Tổng số đo các góc của một đa giác đều cạnh là thì số cạnh là:
Tổng số góc của đa giác đều n cạnh là:
Từ giả thiết ta có:
Cho một lục giác đều và một ngũ giác đều chung cạnh AD như hình vẽ.
Số đo góc 660
Số đo góc 540
Số đo góc 600
Cho một lục giác đều và một ngũ giác đều chung cạnh AD như hình vẽ.
Số đo góc 660
Số đo góc 540
Số đo góc 600
Theo công thức tính góc của đa giác đều ta có:
Ta có: có
cân tại D.
Do đó
Cho hình ngũ giác đều ABCDE tâm O.
Phép quay ngược chiều tâm O góc quay 1440 biến điểm A thành điểm nào dưới đây?
Ta có ABCDE là ngũ giác đều nên
Mà góc quay
=> Phép quay ngược chiều tâm O góc quay 1440 biến điểm A thành điểm C.
Phép quay tâm O (O là tâm hình chữ nhật ABCD) với góc quay bằng bao nhiêu biến hình chữ nhật ABCD thành chính nó?
Vì phép quay và phép quay
giữ nguyên mọi điểm nên đáp án cần tìm là:
.
Cho hình vuông nội tiếp đường tròn tâm . hãy cho biết các phép quay thuận chiều lần lượt với tâm sẽ biến các điểm thành những điểm nào?
|
|
A |
B |
C |
D |
|
900 |
B |
C |
D |
A |
|
1800 |
C |
D |
A |
B |
|
2700 |
D |
A |
B |
C |
Cho hình vuông nội tiếp đường tròn tâm . hãy cho biết các phép quay thuận chiều lần lượt
với tâm
sẽ biến các điểm
thành những điểm nào?
|
|
A |
B |
C |
D |
|
900 |
B |
C |
D |
A |
|
1800 |
C |
D |
A |
B |
|
2700 |
D |
A |
B |
C |
Hình vẽ minh họa
Các phép quay thuận chiều lần lượt là với tâm
biến các điểm
thành những điểm tương ứng cho bởi bảng sau:
Tổng số đo các góc của đa giác đều cạnh bằng:
Tổng số đo các góc của đa giác đều cạnh bằng:
.
Cho ngũ giác đều như hình vẽ.
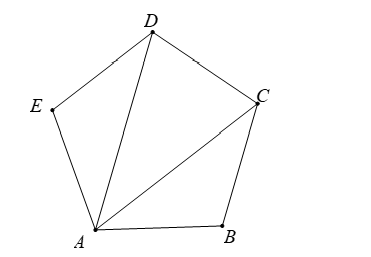
Tính số đo góc E.
Tổng các góc trong của ba tam giác và
là:
Tổng các góc trong của ngũ giác đều
là
.
Vì là ngũ giác đều nên tất cả các góc đều bằng nhau nên số đo mỗi góc của ngũ giác đều bằng
.
Vậy số đo góc E bằng .
Cho tam giác đều như hình vẽ.
Phép phép quay thuận chiều tâm biến điểm B thành điểm C
Cho tam giác đều như hình vẽ.
Phép phép quay thuận chiều tâm
biến điểm B thành điểm C
Tam giác đều nên
. Do đó
thuộc đường tròn
.
Xét đường tròn , ta có:
Khi đó điểm biến thành điểm
qua phép quay thuận chiều
tâm
.
Cho một hình lục giác đều và một hình vuông cùng nội tiếp một đường tròn. Biết rằng hình vuông có cạnh bằng . Tính diện tích của hình lục giác đều đã cho.
Hình vẽ minh họa
Ta có tam giác vuông tại
.
Theo định lí Pythagore, ta có:
hay
Ta có cạnh của hình lục giác đều bằng bán kính đường tròn ngoại tiếp.
Xét tam giác đều cạnh
nên đường cao
.
Do đó diện tích tam giác
Diện tích hình lục giác đều là:
Cho tam giác ABC đều có O là trọng tâm, gọi lần lượt là trung điểm các cạnh . Phép quay thuận chiều tâm O góc quay 120° biến điểm F thành điểm nào dưới đây?
Phép quay thuận chiều tâm O góc quay 120° biến điểm F thành điểm E.
Cho tam giác đều có G là trọng tâm. Phép quay tâm G với quay nào thì biến tam giác ABC thành chính nó?
Do tam giác ABC đều nên AB = BC =AC
Do đó
Vậy các phép quay thuận chiều (hay ngược chiều) tâm G giữ nguyên hình tam giác ABC.
Xét phép quay góc α có tâm là tâm của đa giác đều trên hình. Để biến hình trên thành chính nó thì α không thể bằng:
Các đỉnh của hình trên tạo thành đa giác đều 6 cạnh.
Mỗi góc ở tâm có số đo 3600 : 6 = 600
Các góc quay biến hình trên là chính nó là bội số của 600.
Tính số cạnh của một đa giác đều, biết mỗi góc của nó bằng ?
Gọi số cạnh của đa giác đều là
Ta có:
Vậy đa giác đều đã cho có 8 cạnh.
Một đa giác đều có cạnh, mỗi cạnh có độ dài . Chu vi của đa giác đó là:
Đa giác đều có tất cả các cạnh bằng nhau nên mỗi cạnh của đa giác có số đo bằng
Chu vi của đa giác đều 9 cạnh, mỗi cạnh 4cm là:
