Lớp 8 Toán 8 - Kết nối tri thức với Cuộc sống

Luyện tập Định lí Pythagore và ứng dụng Kết nối tri thức

Khoahoc.vn xin gửi tới bạn đọc bài viết Bài tập Toán lớp 8: Định lí Pythagore và ứng dụng sách Kết nối tri thức. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé!

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 15 câu
  • Điểm số bài kiểm tra: 15 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng
    Tính diện tích tam giác

    Cho tam giác ABC có AB = 14cm,AC = 35cm, đường phân giác AD = 12cm. Diện tích tam giác ABC bằng bao nhiêu?

    Hướng dẫn:

    Hình vẽ minh họa

    Kẻ DE song song với AB và H là hình chiếu của E trên AD.

    Ta có: \frac{AE}{EC} = \frac{BD}{DC} = \frac{AB}{AC}

    \Rightarrow \frac{EA}{35 - EC} = \frac{14}{35}

    \Rightarrow AE = 10cm

    Mặt khác \frac{ED}{AB} = \frac{EC}{AC} \Rightarrow ED = 10cm

    Suy ra tam giác ADE cân tại E \Rightarrow AH = \frac{1}{2}AD = 6cm

    Theo định lí Pythagore ta có:

    EH = \sqrt{AE^{2} - AH^{2}} = 8cm

    Ta có: S_{ADE} = \frac{1}{2}EK.AD = 48cm^{2}

    \Rightarrow S_{ADC} = \frac{AC}{AE}.S_{ADE} = 168cm^{2}

    \frac{BD}{BC} = \frac{AB}{AC} = \frac{14}{35} \Rightarrow \frac{BC}{DC} = \frac{49}{35}

    \Rightarrow S_{ABC} = \frac{BC}{DC}.S_{ADC} = 235,2cm^{2}

  • Câu 2: Thông hiểu
    Xác định tam giác ABC

    Cho \Delta ABC;AC = 15cm, kẻ đường cao AH biết AH = 12cm,BH = 9cm. Xác định dạng của tam giác ABC?

    Hướng dẫn:

    Hình vẽ minh họa:

    Áp dụng định lí Pythagore cho tam giác ABH vuông tại H ta có:

    AB^{2} = AH^{2} + BH^{2}

    \Rightarrow AB^{2} = 12^{2} + 9^{2} = 225

    \Rightarrow AB = 15(cm)

    Vì AB = AC nên tam giác ABC cân tại A.

  • Câu 3: Nhận biết
    Chọn đáp án đúng

    Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:

    Hướng dẫn:

    Ta có:

    15^{2} + 8^{2} = 289 < 324 = 18^{2} nên tam giác này không phải tam giác vuông

    21^{2} + 20^{2} = 841 = 29^{2} nên tam giác này là tam giác vuông

    5^{2} + 6^{2} = 61 < 64 = 8^{2} nên tam giác này không phải tam giác vuông

    2^{2} + 3^{2} = 13 < 16 = 4^{2}nên tam giác này không phải là tam giác vuông

  • Câu 4: Vận dụng cao
    Tìm x

    Cho hình vẽ:

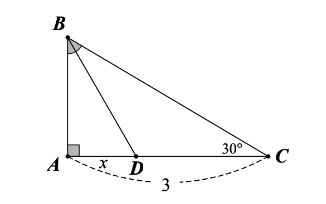
    Định lí Pythagore

    Tính giá trị của x?

    Hướng dẫn:

    Ta có:

    Tam giác ABC vuông tại A nên \widehat{ABC} + \widehat{ACB} = 90^{0}

    \Rightarrow \widehat{ABC} = 90^{0} - \widehat{ACB} = 90^{0} - 30^{0} = 60^{0}

    Ta lại có BD là tia phân giác góc \widehat{ABC} nên \widehat{ABD} = \widehat{DBC} = \frac{\widehat{ABC}}{2} = \frac{60^{0}}{2} = 30^{0}

    Tam giác ABC vuông tại A có \widehat{ACB} = 30^{0} nên AB = \frac{1}{2}BC \Rightarrow BC = 2AB

    Áp dụng định lí Pythagore ta có:

    BC^{2} = AB^{2} + AC^{2}

    \Rightarrow (2AB)^{2} = AB^{2} + 3^{2}

    \Rightarrow 4AB^{2} = AB^{2} + 9

    \Rightarrow AB^{2} = 3 \Rightarrow AB = \sqrt{3}

    Tam giác ABC vuông tại A có: \widehat{ABD} = 30^{0} \Rightarrow AD = \frac{1}{2}BD \Rightarrow BD = 2AD

    Áp dụng định lí Pythagore ta có:

    \Rightarrow BD^{2} = AB^{2} + AD^{2}

    \Rightarrow (2AD)^{2} = 3 + AD^{2}

    \Rightarrow AD^{2} = 1 \Rightarrow AD = 1 \Rightarrow x = 1

  • Câu 5: Thông hiểu
    Tính độ dài cạnh hình thoi

    Tính cạnh hình thoi ABCD, biết AC = 12cm,BD = 16cm.

    Hướng dẫn:

    Hình vẽ minh họa

    Gọi I là giao điểm của AC và BD

    Ta có ABCD là hình thoi

    => \left\{ \begin{matrix} AB = BC = CD = DA \\ AC\bot BD \\ BI = ID \\ AI = IC \\ \end{matrix} ight.

    Dễ dàng chứng minh được \Delta ABI = \Delta BIC = \Delta CID = \Delta DIA

    Áp dụng định lí Pythagore cho tam giác ABI vuông tại I ta có:

    AB^{2} = BI^{2} + IA^{2} \Rightarrow AB = \sqrt{BI^{2} + IA^{2}}

    \Rightarrow AB = \sqrt{6^{2} + 8^{2}} = 10(cm)

  • Câu 6: Thông hiểu
    Chọn đáp án đúng

    Cho tam giác ABC vuông tại A, đường phân giác BD. Biết rằng AD = 3cm,DC = 5cm. Đáp án nào dưới đây đúng?

    Hướng dẫn:

    Hình vẽ minh họa

    Áp dụng định lí Pythagore ta có:

    AB^{2} + AC^{2} = BC^{2}

    \Rightarrow AC^{2} = BC^{2} - AB^{2} = 64

    Do BD là phân giác nên \frac{CB}{CD} = \frac{AB}{AD}

    \frac{CB^{2}}{CD^{2}} = \frac{AB^{2}}{AD^{2}} = \frac{CB^{2} - AB^{2}}{CD^{2} - AD^{2}} = \frac{64}{16}

    \Rightarrow \left\{ \begin{matrix}AB = \dfrac{8.3}{4} = 6cm \\CB = \dfrac{8.5}{4} = 10cm \\\end{matrix} ight.

  • Câu 7: Thông hiểu
    Tính giá trị của x

    Tìm giá trị x trong hình vẽ:

    Hướng dẫn:

    Áp dụng định lí Pythagore cho tam giác ABH vuông tại H ta có:

    AB^{2} = AH^{2} + BH^{2}

    \Rightarrow AH^{2} = AB^{2} - BH^{2} = 9^{2} - 3^{2} = 72

    Áp dụng định lí Pythagore cho tam giác AHC vuông tại H ta có:

    AC^{2} = AH^{2} + CH^{2}

    \Rightarrow HC^{2} = AC^{2} - AH^{2} = 11^{2} - 72 = 49

    \Rightarrow x = HC = \sqrt{49} = 7(cm)

  • Câu 8: Vận dụng
    Tính số đo góc POQ

    Cho tam giác đều MPQ có điểm O nằm bên trong của tam giác thỏa mãn OM^{2} = OP^{2} +OQ^{2}. Tính số đo góc \widehat{POQ}

    Hướng dẫn:

    Hình vẽ minh họa

    Vẽ tam giác đều OPR ta có:

    \left\{ \begin{matrix}\widehat{MPO} + \widehat{OPQ} = 60^{0} \\\widehat{RPQ} + \widehat{OPQ} = 60^{0} \\\end{matrix} ight.\ \Rightarrow \widehat{MPO} =\widehat{RPQ}

    Xét tam giác PMO và tam giác PQR ta có:

    PO = PR

    PM = PQ

    \widehat{MPO} =\widehat{RPQ}

    \Rightarrow \Delta PMO = \Delta PQR(c -g - c)

    \Rightarrow MO = QR

    Khi đó: OM^{2} = OP^{2} + OQ^{2}\Rightarrow QR^{2} = OR^{2} + OQ^{2}

    Theo định lí Pythagore đảo suy ra tam giác OQR vuông tại O.

    Vậy  \widehat{POQ} =90^0+60^0=150^0 

  • Câu 9: Thông hiểu
    Tính độ dài cạnh BK

    Cho tam giác ABC vuông có cạnh huyền AB = \sqrt{117};BC = 6cm. Lấy K là trung điểm của AC. Tính độ dài cạnh BK?

    Hướng dẫn:

    Hình vẽ minh họa

    Áp dụng định lí Pythagore cho tam giác ABC vuông tại C ta có:

    AC^{2} + BC^{2} = AB^{2} \Rightarrow AC = \sqrt{117 - 36} = 9

    \Rightarrow CK = \frac{9}{2}(cm)

    Áp dụng định lí Pythagore cho tam giác BCK vuông tại C nên:

    BK^{2} = BC^{2} + CK^{2} \Rightarrow BK = \sqrt{36 + \frac{81}{4}} = 7,5(cm)

  • Câu 10: Nhận biết
    Tính độ dài BC

    Cho tam giác ABC vuông tại A, AB = 6cm,AC = 8cm. Độ dài cạnh BC là:

    Hướng dẫn:

    Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta có:

    AB^{2} + AC^{2} = BC^{2}

    \Rightarrow BC = \sqrt{AB^{2} + AC^{2}} = \sqrt{6^{2} + 8^{2}} = 10(cm)

  • Câu 11: Nhận biết
    Chọn các đáp án đúng

    Kiểm tra xem tam giác nào là tam giác vuông trong các tam giác có độ dài như sau:

    Hướng dẫn:

    Ta có:

    4^{2} + 6^{2} = 52 eq 49 = 7^{2} nên tam giác này không là tam giác vuông.

    6^{2} + 8^{2} = 100 = 10^{2} nên tam giác này là tam giác vuông

    12^{2} + 16^{2} = 400 = 20^{2} nên tam giác này là tam giác vuông

    6^{2} + 9^{2} = 117 eq 11^{2} nên tam giác này không là tam giác vuông

  • Câu 12: Vận dụng
    Tính độ dài cạnh huyền của tam giác

    Cho tam giác vuông biết độ dài hai cạnh góc vuông có tỉ lệ 3:4 và chu vi bằng 36cm. Tính độ dài cạnh huyền của tam giác

    Kết quả: 15cm

    Đáp án là:

    Cho tam giác vuông biết độ dài hai cạnh góc vuông có tỉ lệ 3:4 và chu vi bằng 36cm. Tính độ dài cạnh huyền của tam giác

    Kết quả: 15cm

    Gọi độ dài hai cạnh góc vuông là x, y ,(x, y > 0)

    Và độ dài cạnh huyền là z, (z > 0)

    Theo bài ra ta có:

    \left\{ \begin{matrix}\dfrac{x}{3} = \dfrac{y}{4} = k,(k > 0) \\x + y + z = 36 \\\end{matrix} ight.\ i,\Rightarrow \left\{ \begin{matrix}x = 3k \\y = 4k \\x + y + z = 36 \\\end{matrix} ight.

    Theo định lí Pythagore ta có:

    x^{2} + y^{2} = z^{2} \Rightarrow z^{2}= (3k)^{2} + (4k)^{2} = (5k)^{2}

    \Rightarrow z = 5k

    x + y + z = 36 \Rightarrow 3k + 4k + 5k= 36 \Rightarrow k = 3(tm)

    Vậy độ dài cạnh huyền là 15cm

  • Câu 13: Vận dụng
    Tính độ dài cạnh tam giác

    Một tam giác vuông có độ dài các cạnh góc vuông tỉ lệ với 5 và 12 và độ dài cạnh huyền bằng 26cm. Độ dài hai cạnh góc vuông là:

    Hướng dẫn:

    Áp dụng định lí Pythagore và tính chất của dãy tỉ số bằng nhau

    Gọi độ dài hai cạnh góc vuông là x và y (x, y > 0)

    Theo định lí Pythagore ta có:

    x^{2} + y^{2} = 26^{2}

    Theo bài ra ta có:

    \frac{x}{5} = \frac{y}{12} \Rightarrow \frac{x^{2}}{25} = \frac{y^{2}}{144} = \frac{x^{2} + y^{2}}{25 + 144} = \frac{676}{169} = 4

    \Rightarrow \left\{ \begin{matrix} x^{2} = 25.4 = 100 \Rightarrow x = 10cm \\ y^{2} = 144.4 = 576 \Rightarrow y = 24cm \\ \end{matrix} ight.

  • Câu 14: Thông hiểu
    Điền đáp án vào chỗ trống

    Cho tam giác ABC vuông tại A có AB = 6cm,AC = 8cm . Kẻ đường cao AH. Biết AH = 4,8cm . Khi đó:

    Độ dài cạnh BH là: 3,6cm

    Độ dàu cạnh CH là: 6,4cm

    (Kết quả ghi dưới dạng số thập phân)

    Đáp án là:

    Cho tam giác ABC vuông tại A có AB = 6cm,AC = 8cm . Kẻ đường cao AH. Biết AH = 4,8cm . Khi đó:

    Độ dài cạnh BH là: 3,6cm

    Độ dàu cạnh CH là: 6,4cm

    (Kết quả ghi dưới dạng số thập phân)

    Hình vẽ minh họa

    Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta có:

    A{B^2} + A{C^2} = B{C^2} \Rightarrow BC = 10\left( {cm} ight)

    Áp dụng định lí Pythagore cho tam giác ABH vuông tại H ta có:

    AB^{2} = AH^{2} + BH^{2}

    \Rightarrow BH^{2} = AB^{2} -AH^{2}

    \Rightarrow BH^{2} = 6^{2} - (4,8)^{2} =12,96

    \Rightarrow BH = 3,6(cm)

    Suy ra HC = BC - BH = 6,4cm

  • Câu 15: Thông hiểu
    Xác định tam giác ABC

    Cho tam giác ABC, đường cao AH. Xác định tam giác ABC biết AH = 6cm,BH = 4,5cm,HC = 8cm?

    Hướng dẫn:

    Hình vẽ minh họa

    Áp dụng định lí Pythagore cho tam giác ABH vuông tại H ta có:

    AB^{2} = AH^{2} + BH^{2}

    \Rightarrow AB^{2} = 6^{2} + (4,5)^{2} = \frac{225}{4}

    \Rightarrow AB = \sqrt{\frac{225}{4}} = 7,5(cm)

    Áp dụng định lí Pythagore cho tam giác ACH vuông tại H ta có:

    AC^{2} = AH^{2} + CH^{2}

    \Rightarrow AC^{2} = 6^{2} + 8^{2} = 100

    \Rightarrow AC = 10cm

    Xét tam giác ABC có:

    AB^{2} + AC^{2} = (7,5)^{2} + 10^{2} = \frac{625}{4} = (12,5)^{2} = BC^{2}

    Vậy tam giác ABC vuông tại A

0/15
15 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (20%):
    2/3
  • Thông hiểu (47%):
    2/3
  • Vận dụng (27%):
    2/3
  • Vận dụng cao (7%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 20 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 8 KNTT

Đăng nhập