Lớp 12 Toán 12

Luyện tập Phép cộng, trừ và nhân số phức (Trung bình)

Hãy cùng Luyện tập củng cố các phép tính với số phức ngay các em nhé!

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng
    Tìm số phức z thỏa mãn điều kiện

    Cho z1 = 1 + i; z2 = -1 - i. Tìm {z_3} \in \mathbb{C} sao cho các điểm biểu diễn của {z_1};\,\,{z_2};\,\,{z_3} tạo thành tam giác đều.

    Hướng dẫn:

     Giả sử {z_3} = x + yi

    Để các điểm biểu diễn của {z_1};\,\,{z_2};\,\,{z_3} tạo thành một tam giác đều thì

    \left\{ {\begin{array}{*{20}{c}} {\left| {{z_1} - {z_2}} ight| = \left| {{z_1} - {z_3}} ight|} \\ {\left| {{z_1} - {z_2}} ight| = \left| {{z_2} - {z_3}} ight|} \end{array}} ight.

    \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\sqrt {4 + 4} = \sqrt {{{\left( {x - 1} ight)}^2} + {{\left( {y - 1} ight)}^2}} } \\ {\sqrt {4 + 4} = \sqrt {{{\left( {x + 1} ight)}^2} + {{\left( {y + 1} ight)}^2}} } \end{array}} ight.

    \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{{\left( {x - 1} ight)}^2} + {{\left( {y - 1} ight)}^2} = 8} \\ {x + y = 0} \end{array}} ight.

    \Rightarrow 2{y^2} = 6 \Rightarrow y = \pm \sqrt 3 \Rightarrow x = \mp \sqrt 3

    Vậy có hai số phức thoả mãn là: {z_3} = {\text{\{ }}\sqrt 3 - \sqrt 3 i;\,\, - \sqrt 3 + \sqrt 3 i\}

  • Câu 2: Vận dụng
    Số phức có mô đun nhỏ nhất

    Trong các số phức z thỏa mãn điều kiện \left| {z - 2 - 4i} ight| = \left| {z - 2i} ight|. Số phức z có mô đun bé nhất bằng

    Hướng dẫn:

     Đặt z = x + yi{\mkern 1mu} {\mkern 1mu} \left( {x,y \in \mathbb{R}} ight)

    Khi đó \left| {z - 2 - 4i} ight| = \left| {z - 2i} ight|

    \Leftrightarrow \left| {x + yi - 2 - 4i} ight| = \left| {x + yi - 2i} ight|

    \Leftrightarrow {\left( {x - 2} ight)^2} + {\left( {y - 4} ight)^2} = {x^2} + {\left( {y - 2} ight)^2}

    \Leftrightarrow - 4x - 4y + 16 = 0

    \Leftrightarrow x + y - 4 = 0

    Số phức có mô đun nhỏ nhất bằng khoảng cách từ đến đường thẳng \Delta :x + y - 4 = 0.

    {\left| z ight|_{\min }} = d\left( {O;\Delta } ight) = \frac{{\left| 4 ight|}}{{\sqrt 2 }} = 2\sqrt 2

  • Câu 3: Nhận biết
    Xác định số phức z

    Cho hai số phức {z_1} = 5 - 7i và {z_2} = 2 + 3i. Tìm số phức z = {z_1} + {z_2}

    Hướng dẫn:

     Ta có:

    \begin{matrix} z = {z_1} + {z_2} \hfill \\ = \left( {5 - 7i} ight) + \left( {2 + 3i} ight) \hfill \\ = (5 + 2) + ( - 7 + 3)i \hfill \\ = 7 - 4i \hfill \\ \end{matrix}

  • Câu 4: Vận dụng cao
    Giá trị lớn nhất của biểu thức

    Cho số phức z thỏa mãn điêu kiện \left| {z - 1} ight| = \sqrt 2. Tính giá trị lớn nhất của biểu thức T = \left| {z + i} ight| + \left| {z - 2 - i} ight|

    Hướng dẫn:

    Đặt z = x + yi\left( {x,y \in \mathbb{R}} ight), ta có:

    \left| {z - 1} ight| = \sqrt 2 \Leftrightarrow \left| {x - 1 + yi} ight| = \sqrt 2

    \Leftrightarrow {\left( {x - 1} ight)^2} + {y^2} = 2 \Leftrightarrow {x^2} + {y^2} = 2x + 1\left( * ight)

    Mặt khác: T = \left| {z + i} ight| + \left| {z - 2 - i} ight| = \left| {x + \left( {y + 1} ight)i} ight| + \left| {x - 2} ight| + \left( {y - 1} ight)i

    = \sqrt {{x^2} + {{\left( {y + 1} ight)}^2}} + \sqrt {{{\left( {x - 2} ight)}^2} + {{\left( {y - 1} ight)}^2}}

    = \sqrt {{x^2} + {y^2} + 2y + 1} + \sqrt {{x^2} + {y^2} - 4x - 2y + 5}

    Kết hợp với (*), ta được:

    T = \sqrt {2x + 2y + 2} + \sqrt {6 - 2x - 2y}

    Áp dụng bất đẳng thức Bunhacopxki ta được

    T \leqslant \sqrt {\left( {{1^2} + {1^2}} ight)\left[ {{{\left( {\sqrt {2x + 2y + 2} } ight)}^2} + {{\left( {\sqrt {6 - 2x - 2y} } ight)}^2}} ight]} = 4

    Vậy \max T = 4

  • Câu 5: Thông hiểu
    Mô đun số phức w bằng bao nhiêu?

    Cho số phức z = - \frac{1}{2} + \frac{{\sqrt 3 }}{2}i. Số phức w = 1 + z + {z^2},\left| w ight| bằng:

    Hướng dẫn:

     Ta có: \left| w ight| = \left| {1 + z + {z^2}} ight| = \left| {1 - \frac{1}{2} + \frac{{\sqrt 3 }}{2}i - \frac{1}{2} - \frac{{\sqrt 3 }}{2}i} ight| = 0

  • Câu 6: Thông hiểu
    Tìm x, y thỏa mãn điều kiện

    Tìm các số thực x, y thoả mãn:

    3x + y + 5xi = 2y – 1 +(x – y)i

    Hướng dẫn:

    Theo giả thiết: 3x + y + 5xi = 2y – 1 +(x – y)i

    => (3x + y) + (5x)i = (2y – 1) +(x – y)i

    =>\left\{ \begin{gathered} 3x + y = 2y - 1 \hfill \\ 5x = x - y \hfill \\ \end{gathered} ight.

    => \left\{ \begin{gathered} x = - \frac{1}{7} \hfill \\ y = \frac{4}{7} \hfill \\ \end{gathered} ight.

  • Câu 7: Thông hiểu
    Căn bậc hai của số phức

    Tìm các căn bậc hai của số phức z = 5 + 12i

    Hướng dẫn:

     Giả sử m + ni (m; n \in R) là căn bậc hai của z

    Ta có: {(m + ni)^2} = 5 + 12i

    \Leftrightarrow {m^2} + 2mni + {n^2}{i^2} = 5 + 12i \Leftrightarrow {m^2} + 2mni - {n^2} = 5 + 12i

    \Leftrightarrow \left\{ \begin{gathered} {m^2} - {n^2} = 5 \hfill \\ 2mn = 12 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} {m^2} - {n^2} = 5(1) \hfill \\ m = \frac{6}{n}(2) \hfill \\ \end{gathered} ight.

    Thay (2) vào (1) ta có: {\left( {\frac{6}{n}} ight)^2} - {n^2} = 5 \Leftrightarrow 36 - {n^4} = 5{n^2}

    \Leftrightarrow {n^4} + 5{n^2} - 36 = 0 \Leftrightarrow {n^2} = 4;{n^2} = - 9(loai)

    \left[ \begin{gathered} n = 2 \Rightarrow m = 3 \hfill \\ n = - 2 \Rightarrow m = - 3 \hfill \\ \end{gathered} ight.

    Vậy z có hai căn bậc hai là 3+2i và -3-2i.

  • Câu 8: Vận dụng
    Chọn khẳng định đúng

    Cho số phức w = x + yi;\left( {x,y \in \mathbb{R}} ight) thoả điều kiện \left| {{w^2} + 4} ight| = 2\left| w ight|.

    Đặt P = 8\left( {{x^2} - {y^2}} ight) + 12. Khẳng định nào sau đây đúng?

    Hướng dẫn:

     Ta có:

    \left| {{w^2} + 4} ight| = 2\left| w ight| \Leftrightarrow \left| {{x^2} - {y^2} + 4 + 2xyi} ight| = 2\left| {x + yi} ight|

    \Leftrightarrow {\left( {{x^2} - {y^2} + 4} ight)^2} + 4{x^2}{y^2} = 4\left( {{x^2} + {y^2}} ight)

    \begin{matrix} \Leftrightarrow {x^4} + {y^4} + 16 + 2{x^2}{y^2} + 4{x^2} - 12{y^2} = 0 \hfill \\ \Leftrightarrow {x^4} + {y^4} + 2{x^2}{y^2} - 4{x^2} - 4{y^2} + 4 + 8\left( {{x^2} - {y^2}} ight) + 12 = 0 \hfill \\ \end{matrix}

    \begin{matrix} \Leftrightarrow 8\left( {{x^2} - {y^2}} ight) + 12 = - \left( {{x^4} + {y^4} + 2{x^2}{y^2} - 4{x^2} - 4{y^2} + 4} ight) \hfill \\ \Leftrightarrow P = - {\left( {{x^2} + {y^2} - 2} ight)^2} = - {\left( {{{\left| {\text{w}} ight|}^2} - 2} ight)^2}. \hfill \\ \end{matrix}

    Nhận xét: câu này đáp án A cũng đúng vì \left| {\text{w}} ight| = \left| {\overline {\text{w}} } ight|.

  • Câu 9: Thông hiểu
    Xác định số phức

    Số phức z thỏa mãn: \left( {1 + i} ight)z + \left( {2 - 3i} ight)\left( {1 + 2i} ight) = 7 + 3i là:

    Hướng dẫn:

     Ta áp dụng các quy tắc thực hiện phép tính, có:

    \begin{matrix} \left( {1 + i} ight)z + \left( {2 - 3i} ight)\left( {1 + 2i} ight) = 7 + 3i \hfill \\ \Leftrightarrow (1 + i)z = 7 + 3i - (2 - 3i)(1 + 2i) \hfill \\ \Leftrightarrow (1 + i)z = - 1 + 2i \hfill \\ \Leftrightarrow z = \dfrac{{ - 1 + 2i}}{{1 + i}} \hfill \\ \Leftrightarrow z = \dfrac{1}{2} + \dfrac{3}{2}i \hfill \\ \end{matrix}

    Ngoài ra ta có thể sử dụng lệnh CALC trong máy tính để thử các phương án.

  • Câu 10: Vận dụng
    Xác định tham số m thỏa mãn điều kiện

    Cho hai số phức z, w thỏa mãn \left| {z - 1} ight| = \left| {z + 3 - 2i} ight|; w = z + m + i với m \in \mathbb{R} là tham số. Giá trị của m để ta luôn có \left| w ight| \geqslant 2\sqrt 5 là:

    Hướng dẫn:

     Đặt z = a + ib,\left( {a,b \in \mathbb{R}} ight) có biểu diễn hình học là điểm M\left( {x;y} ight)

    Ta có:

    \left| {z - 1} ight| = \left| {z + 3 - 2i} ight|

    \Leftrightarrow \left| {x - 1 + iy} ight| = \left| {x + 3 + \left( {y - 2} ight)i} ight|

    \Leftrightarrow \sqrt {{{\left( {x - 1} ight)}^2} + {y^2}} = \sqrt {{{\left( {x + 3} ight)}^2} + {{\left( {y - 2} ight)}^2}}

    \Leftrightarrow - 2x + 1 = 6x + 9 - 4y + 4 \Leftrightarrow 2x - y + 3 = 0

    Suy ra biểu diễn của số phức là đường thẳng \Delta :2x - y + 3 = 0

    Ta xét: \left| \omega ight| \geqslant 2\sqrt 5 \Leftrightarrow \left| {z + m + i} ight| \geqslant 2\sqrt 5 \Leftrightarrow \left| {x + m + + \left( {y + 1} ight)i} ight| \geqslant 2\sqrt 5

    với I\left( { - m; - 1} ight).

    Mà ta có MI \geqslant d\left( {I,\Delta } ight)

    Nên MI \geqslant 2\sqrt 5 \Leftrightarrow d\left( {I,\Delta } ight) \geqslant 2\sqrt 5 \Leftrightarrow \frac{{\left| { - 2m + 4} ight|}}{{\sqrt 5 }} \geqslant 2\sqrt 5 \Leftrightarrow \left| { - 2m + 4} ight| \geqslant 10

    \Leftrightarrow \left[ \begin{gathered} - 2m + 4 \geqslant 10 \hfill \\ - 2m + 4 \leqslant - 10 \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} m \leqslant - 3 \hfill \\ m \geqslant 7 \hfill \\ \end{gathered} ight.

  • Câu 11: Nhận biết
    Tìm số phức z

    Tìm số phức z thỏa mãn z + 2 - 3i = 3 - 2i

    Hướng dẫn:

     Ta có z + 2 - 3i = 3 - 2i \Leftrightarrow z = 3 - 2i - 2 + 3i = 1 + i

  • Câu 12: Thông hiểu
    Tính mô đun số phức

    Cho hai số phức {z_1} = 2 + i,{z_2} = 3 - 4i. Môđun của số phức \left( {{z_1} - {z_2}} ight) là:

    Hướng dẫn:

     Ta có: \left| {{z_1} - {z_2}} ight| = \left| {2 + i - 3 + 4i} ight| = \left| { - 1 + 5i} ight| = \sqrt {26}

  • Câu 13: Nhận biết
    Tìm số phức z

    Cho hai số phức {z_1} = 4 - 3i và {z_2} = 7 + 3i. Tìm số phức z = {z_1} - {z_2}

    Hướng dẫn:

     Ta có:

    \begin{matrix} z = {z_1} - {z_2} \hfill \\ = \left( {4 - 3i} ight) - \left( {7 + 3i} ight) \hfill \\ = 4 - 3i - 7 - 3i \hfill \\ = (4 - 7) + ( - 3 - 3)i \hfill \\ = - 3 - 6i \hfill \\ \end{matrix}

  • Câu 14: Nhận biết
    Tính giá trị biểu thức P

    Cho số phức z = a + bi,\left( {a,b \in \mathbb{R}} ight) thỏa mãn \left( {1 + i} ight)z + 2\overline z = 3 + 2i. Tính P = a + b

    Hướng dẫn:

    Giả sử: z = a + bi{\text{ }}\left( {a,b \in \mathbb{R}} ight)

    \left( {1 + i} ight)\left( {a + bi} ight) + 2\left( {a - bi} ight) = 3 + 2i

    \Leftrightarrow 3a - b + \left( {a - b} ight)i = 3 + 2i

    \Leftrightarrow \left\{ \begin{gathered} 3a - b = 3 \hfill \\ a - b = 2 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} a = \frac{1}{2} \hfill \\ b = - \frac{3}{2} \hfill \\ \end{gathered} ight.

    \Rightarrow P = a + b = - 1

  • Câu 15: Vận dụng
    Tính giá trị biểu thức

    Cho số phức z = a + bi , \left( {a,b \in \mathbb{R}} ight)thỏa mãn \left( {z + 1 + i} ight)\left( {\overline z - i} ight) + 3i = 9 và \left| {\overline z } ight| > 2.

    Tính P = a + b.

    Hướng dẫn:

     Ta áp dụng công thức z = a + bi \Rightarrow \overline z = a - bi, có:

    \left( {z + 1 + i} ight)\left( {\overline z - i} ight) + 3i = 9

    \Leftrightarrow \left( {a + bi + 1 + i} ight)\left( {a - bi - i} ight) + 3i = 9

    \Leftrightarrow {a^2} + {b^2} + 2b + a + 1 - \left( {b + 1} ight)i = 9 - 3i

    Ta xét: \left\{ \begin{gathered} {a^2} + {b^2} + 2b + a + 1 = 9 \hfill \\ b + 1 = 3 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} b = 2 \hfill \\ {a^2} + a = 0 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} b = 2 \hfill \\ a = 0 \hfill \\ \end{gathered} ight. \vee \left\{ \begin{gathered} b = 2 \hfill \\ a = - 1 \hfill \\ \end{gathered} ight.

    Với {z_1} = 2i \Rightarrow \left| {{z_1}} ight| = 2 nên không thỏa yêu cầu bài toán.

    Với {z_2} = - 1 + 2i \Rightarrow \left| {{z_2}} ight| = \sqrt {{2^2} + {1^2}} = \sqrt 5 thỏa yêu cầu bài toán.

    Vậy P = a + b = 1

  • Câu 16: Nhận biết
    Tìm phần ảo của số phức

    Cho hai số phức {z_1} = 1 - 3i và {z_2} = - 2 - 5i. Tìm phần ảo b của số phức z = {z_1} - {z_2}. 

    Hướng dẫn:

     Ta có:

    \begin{matrix} z = {z_1} - {z_2} \hfill \\ = \left( {1 - 3i} ight) - \left( { - 2 - 5i} ight) \hfill \\ = 1 - 3i + 2 + 5i \hfill \\= (1 + 2) + ( - 3 + 5)i \hfill \\ \,\,\,\, = 3 + 2i \hfill \\ \end{matrix}

  • Câu 17: Thông hiểu
    Tìm số phức z

    Số phức z = \frac{{3 - 4i}}{{4 - i}} bằng:

    Hướng dẫn:

     Ta có: z = \frac{{3 - 4i}}{{4 - i}} = \frac{{16}}{{17}} - \frac{{13}}{{17}}i

  • Câu 18: Vận dụng cao
    Tính giá trị của biểu thức P

    Cho {z_1},{\text{ }}{z_2} là hai số phức thỏa mãn phương trình \left| {2z - i} ight| = \left| {2 + iz} ight|, biết \left| {{z_1} - {z_2}} ight| = 1

    Tính giá trị của biểu thức: P = \left| {{z_1} + {z_2}} ight|

    Hướng dẫn:

    Cách 1. Ta có:

    \left| {2z - i} ight| = \left| {2 + iz} ight| \Leftrightarrow {\left| {2z - i} ight|^2} = {\left| {2 + iz} ight|^2} \Leftrightarrow (2z - i)(2\overline z + i) = (2 + iz)(2 - i\overline z )

    \Leftrightarrow 4z.\overline z + 2iz - 2i\overline z - {i^2} = 4 - 2i\overline z + 2iz - {i^2}z.\overline z \Leftrightarrow 3z.\overline z = 3

    \Leftrightarrow z.\overline z = 1 \Leftrightarrow {\left| z ight|^2} = 1 \Rightarrow \left| z ight| = 1 \Rightarrow \left| {{z_1}} ight| = 1 và \left| {{z_2}} ight| = 1

    Chú ý: a.\overline a = {a^2} \Rightarrow {\left| {2z - i} ight|^2} = (2z - i)(\overline {2z - i} ) = (2z - i)(2\overline z + i)

    Tập hợp điểm biểu diễn số phức {z_1},{\text{ }}{z_2} là đường tròn tâm O bán kính R = 1.

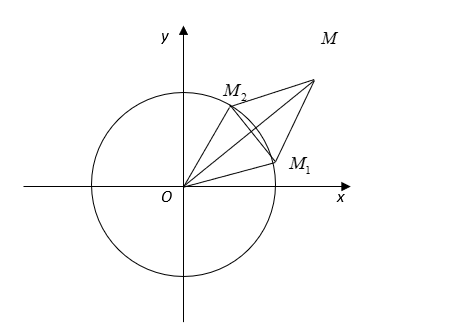
    Tính giá trị của biểu thức P

    Gọi {M_1}({z_1}),{\text{ }}{M_2}({z_2}) \Rightarrow O{M_1} = O{M_2} = 1

    Ta có: \left| {{z_1} - {z_2}} ight| = \left| {\overrightarrow {O{M_1}} - \overrightarrow {O{M_2}} } ight| = \left| {\overrightarrow {{M_2}{M_1}} } ight| = 1 \Rightarrow \Delta O{M_1}{M_2} đều

    Mà \left| {{z_1} + {z_2}} ight| = \left| {\overrightarrow {O{M_1}} + \overrightarrow {O{M_2}} } ight| = \left| {\overrightarrow {OM} } ight| = OM với M là điểm thỏa

    mãn là hình thoi cạnh 1\Rightarrow OM = \sqrt 3 \Rightarrow P = \sqrt 3

    Cách 2. Đặt z = x + yi,{\text{ }}\left( {x,y \in \mathbb{R}} ight), ta có 2z - i = 2x + (2y - 1)i và 2 + iz = 2 - y + xi

    Khi đó:

    \left| {2z - i} ight| = \left| {2 + iz} ight| \Leftrightarrow \sqrt {4{x^2} + {{(2y - 1)}^2}} = \sqrt {{{(y - 2)}^2} + {x^2}} \Leftrightarrow {x^2} + {y^2} = 1

    \Rightarrow \left| z ight| = 1 \Rightarrow \left\{ \begin{gathered} \left| {{z_1}} ight| = 1 \hfill \\ \left| {{z_2}} ight| = 1 \hfill \\ \end{gathered} ight.

    Sử dụng công thức 

    {\left| {{z_1} + {z_2}} ight|^2} + {\left| {{z_1} - {z_2}} ight|^2} = 2\left( {{{\left| {{z_1}} ight|}^2} + {{\left| {{z_2}} ight|}^2}} ight) \Rightarrow {\left| {{z_1} + {z_2}} ight|^2} = 3 \Rightarrow \left| {{z_1} + {z_2}} ight| = \sqrt 3

     

  • Câu 19: Vận dụng
    Tính giá trị biểu thức P

    Cho số phức {z_1},{z_2} thỏa mãn \left| {z + 2 - i} ight| = 2\left| {z - 1 - i} ight| và {z_1} + {z_2} = 1 + i.

    Tính giá trị biểu thức P = {\left| {{z_1}} ight|^2} + {\left| {{z_2}} ight|^2}.

    Hướng dẫn:

     Ta có \left| {{z_1} + 2 - i} ight| = 2\left| {{z_1} - 1 - i} ight| mà {z_1} + {z_2} = 1 + i

    \Rightarrow \left| {{z_1} + 2 - i} ight| = 2\left| {{z_2}} ight|

    \Rightarrow 4{\left| {{z_2}} ight|^2} = \left( {{z_1} + 2 - i} ight)\left( {\overline {{z_1}} + 2 + i} ight) = {\left| {{z_1}} ight|^2} + \left( {2 - i} ight)\overline {{z_1}} + \left( {2 + i} ight){z_1} + 5.(1)

    Tương tự ta có

    4{\left| {{z_1}} ight|^2} = {\left| {{z_2}} ight|^2} + \left( {2 - i} ight)\overline {{z_2}} + \left( {2 + i} ight){z_2} + 5.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( 2 ight)

    Cộng (1) và (2) ta có:

    4P = P + \left( {2 - i} ight)\overline {{z_1} + {z_2}} + \left( {2 + i} ight)\left( {{z_1} + {z_2}} ight) + 10

    = P + \left( {2 - i} ight)\left( {1 - i} ight) + \left( {2 + i} ight)\left( {1 + i} ight) + 10 = P + 12 \Rightarrow P = 4.

  • Câu 20: Nhận biết
    Xác định phần thực và phần ảo của số phức z

    Cho số phức z = 1 - i + {i^3}. Tìm phần thực a và phần ảo b của z.

    Hướng dẫn:

     Ta có z = 1 - i + {i^3} = 1 - i - i = 1 - 2i \Rightarrow a = 1,b = - 2

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (30%):
    2/3
  • Thông hiểu (30%):
    2/3
  • Vận dụng (30%):
    2/3
  • Vận dụng cao (10%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12

Đăng nhập