Lớp 12 Toán 12

Luyện tập Phương trình mũ và phương trình lôgarit (Trung bình)

Hãy cùng Luyện tập củng cố các bài tập Trắc nghiệm Phương trình mũ và phương trình lôgarit các em nhé!

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Thông hiểu
    Tìm x là nghiệm của PT

    Phương trình \ln \frac{{x - 1}}{{x + 8}} = \ln x có nghiệm là: 

    Hướng dẫn:

    Ta có:  \ln \frac{{x - 1}}{{x + 8}} = \ln x \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ \frac{{x - 1}}{{x + 8}} = x \hfill \\ \end{gathered} ight.

    \Rightarrow \left\{ \begin{gathered} x > 0 \hfill \\ \left[ \begin{gathered} x = 4 \hfill \\ x = - 2 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Leftrightarrow x = 4

  • Câu 2: Nhận biết
    Giải PT Logarit

    Phương trình {\log _2}(x + 3) + {\log _2}(x - 1) = {\log _2}5 có nghiệm là:

    2 || hai || x=2 || Hai

    Đáp án là:

    Phương trình {\log _2}(x + 3) + {\log _2}(x - 1) = {\log _2}5 có nghiệm là:

    2 || hai || x=2 || Hai

     PT \Leftrightarrow \left\{ \begin{gathered} x - 1 > 0 \hfill \\ (x + 3)(x - 1) = 5 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > 1 \hfill \\ {x^2} + 2x - 8 = 0 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} x > 1 \hfill \\ \left[ \begin{gathered} x = - 8 \hfill \\ x = 2 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Rightarrow x = 2

  • Câu 3: Nhận biết
    Đếm số nghiệm

    Số nghiệm của phương trình {\log _2}x.{\log _3}(2x - 1) = 2{\log _2}x là:

    2 || hai nghiệm || Hai nghiệm || 2 nghiệm

    Đáp án là:

    Số nghiệm của phương trình {\log _2}x.{\log _3}(2x - 1) = 2{\log _2}x là:

    2 || hai nghiệm || Hai nghiệm || 2 nghiệm

     PT \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ 2x - 1 > 0 \hfill \\ {\log _2}x.{\log _3}(2x - 1) = 2{\log _2}x \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > \frac{1}{2} \hfill \\ {\log _2}x\left[ {{{\log }_3}(2x - 1) - 2} ight] = 0 \hfill \\ \end{gathered} ight. 

    \Leftrightarrow \left\{ \begin{gathered} x > \frac{1}{2} \hfill \\ \left[ \begin{gathered} {\log _2}x = 0 \hfill \\ {\log _3}(2x - 1) = 2 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} x > \frac{1}{2} \hfill \\ \left[ \begin{gathered} x = 1 \hfill \\ x = 5 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ x = 5 \hfill \\ \end{gathered} ight.

    Vậy PT có hai nghiệm.

  • Câu 4: Vận dụng
    Tính tổng 2 nghiệm

    Gọi x_1, x_2 là 2 nghiệm của phương trình {\log _2}\left[ {x\left( {x + 3} ight)} ight] = 1. Khi đó x_1 + x_2 bằng: 

    -3

    Đáp án là:

    Gọi x_1, x_2 là 2 nghiệm của phương trình {\log _2}\left[ {x\left( {x + 3} ight)} ight] = 1. Khi đó x_1 + x_2 bằng: 

    -3

    Điều kiện: \left[ \begin{gathered} x < - 3 \hfill \\ x > 0 \hfill \\ \end{gathered} ight.

    {\log _2}\left[ {x\left( {x + 3} ight)} ight] = 1 \Leftrightarrow x\left( {x + 3} ight) = 2 \Leftrightarrow {x^2} + 3x - 2 = 0

    Vậy {x_1} + {x_2} = - 3.

  • Câu 5: Vận dụng
    Khẳng định đúng?

    Cho phương trình {\left( {7 + 4\sqrt 3 } ight)^x} + {\left( {2 + \sqrt 3 } ight)^x} = 6. Khẳng định nào sau đây là đúng?

    Hướng dẫn:

     Ta có: {\left( {7 + 4\sqrt 3 } ight)^x} + {\left( {2 + \sqrt 3 } ight)^x} = 6

    \Leftrightarrow {\left[ {{{\left( {2 + \sqrt 3 } ight)}^2}} ight]^x} + {\left( {2 + \sqrt 3 } ight)^x} - 6 = 0

    \Leftrightarrow {\left[ {{{\left( {2 + \sqrt 3 } ight)}^x}} ight]^2} + {\left( {2 + \sqrt 3 } ight)^x} - 6 = 0{\text{ }}\left( {*} ight)

    Đặt t = {\left( {2 + \sqrt 3 } ight)^x} > 0.

    Khi đó \left( {*} ight) \Leftrightarrow {t^2} + t - 6 = 0 \Leftrightarrow \left[ \begin{gathered} t = 2{\text{ }}\left( TM ight) \hfill \\ t = - 3{\text{ }}\left( L ight) \hfill \\ \end{gathered} ight.

    Với t = 2 \Rightarrow {\left( {2 + \sqrt 3 } ight)^x} = 2 \Leftrightarrow \boxed{x = {{\log }_{\left( {2 + \sqrt 3 } ight)}}2}.

  • Câu 6: Vận dụng
    Chọn phát biểu đúng

    Phương trình {2^{x - 3}} = {3^{{x^2} - 5x + 6}} có hai nghiệm x_1, x_2 trong đó x_1 < x_2, hãy chọn phát biểu đúng?

    Hướng dẫn:

     Logarit hóa hai vế của phương trình (theo cơ số 2) ta được:

    {2^{x - 3}} = {3^{{x^2} - 5x + 6}} \Leftrightarrow {\log _2}{2^{x - 3}} = {\log _2}{3^{{x^2} - 5x + 6}}

    \Leftrightarrow \left( {x - 3} ight){\log _2}2 = \left( {{x^2} - 5x + 6} ight){\log _2}3

    \Leftrightarrow \left( {x - 3} ight) - \left( {x - 2} ight)\left( {x - 3} ight){\log _2}3 = 0

    \Leftrightarrow \left( {x - 3} ight).\left[ {1 - \left( {x - 2} ight){{\log }_2}3} ight] = 0 \Leftrightarrow \left[ \begin{gathered} x - 3 = 0 \hfill \\ 1 - \left( {x - 2} ight){\log _2}3 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left[ \begin{gathered} x = 3 \hfill \\ \left( {x - 2} ight){\log _2}3 = 1 \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = 3 \hfill \\ x - 2 = \frac{1}{{{{\log }_2}3}} \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left[ \begin{gathered} x = 3 \hfill \\ x = {\log _3}2 + 2 \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = 3 \hfill \\ x = {\log _3}2 + {\log _3}9 \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = 3 \hfill \\ x = {\log _3}18 \hfill \\ \end{gathered} ight.

  • Câu 7: Vận dụng
    Tìm họ nghiệm

    Phương trình {9^{{{\sin }^2}x}} + {9^{{{\cos }^2}x}} = 6 có họ nghiệm là ?

    Hướng dẫn:

     Ta có: {9^{{{\sin }^2}x}} + {9^{{{\cos }^2}x}} = 6

    \Leftrightarrow {9^{1 - {{\cos }^2}x}} + {9^{{{\cos }^2}x}} = 6 \Leftrightarrow \frac{9}{{{9^{{{\cos }^2}x}}}} + {9^{{{\cos }^2}x}} - 6 = 0{\text{ }}\left( * ight)

    Đặt t = {9^{{{\cos }^2}x}},{\text{ }}\left( {1 \leqslant t \leqslant 9} ight).

    Khi đó: \left( * ight) \Leftrightarrow \frac{9}{t} + t - 6 = 0 \Leftrightarrow {t^2} - 6t + 9 = 0 \Leftrightarrow t = 3.

    Với t = 3 \Rightarrow {9^{{{\cos }^2}x}} = 3 \Leftrightarrow {3^{2{{\cos }^2}x}} = {3^1} \Leftrightarrow 2{\cos ^2}x - 1 = 0

    \Leftrightarrow \cos 2x = 0 \Leftrightarrow \boxed{x = \frac{\pi }{4} + \frac{{k\pi }}{2}},{\text{ }}\left( {k \in \mathbb{Z}} ight).

  • Câu 8: Thông hiểu
    Nghiệm lớn nhất

    Nghiệm lớn nhất của phương trình - {\log ^3}x + 2{\log ^2}x = 2 - \log x  là:

    100 || 1 trăm || một trăm || Một trăm || x=100

    Đáp án là:

    Nghiệm lớn nhất của phương trình - {\log ^3}x + 2{\log ^2}x = 2 - \log x  là:

    100 || 1 trăm || một trăm || Một trăm || x=100

     Điều kiện: x>0

    - {\log ^3}x + 2{\log ^2}x = 2 - \log x \Leftrightarrow \left[ \begin{gathered} \log x = - 1 \hfill \\ \log x = 2 \hfill \\ \log x = 1 \hfill \\ \end{gathered} ight.\Leftrightarrow \left[ \begin{gathered} x = \frac{1}{{10}} \hfill \\ x = 100 \hfill \\ x = 10 \hfill \\ \end{gathered} ight.

    Vậy nghiệm lớn nhất là x =100.

  • Câu 9: Nhận biết
    Giải PT Logarit

    Phương trình {\log _3}({x^2} - 6) = {\log _3}(x - 2) + 1 có tập nghiệm là:

    Hướng dẫn:

     PT \Leftrightarrow \left\{ \begin{gathered} {x^2} - 6 > 0 \hfill \\ x - 3 > 0 \hfill \\ {x^2} - 6 = 3(x - 3) \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x < - \sqrt 6 \vee x > \sqrt 6 \hfill \\ x > 3 \hfill \\ \left[ \begin{gathered} x = 0 \hfill \\ x = 3 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Rightarrow x \in \emptyset.

  • Câu 10: Thông hiểu
    Tìm nghiệm nguyên nhỏ nhất

    Nghiệm nguyên nhỏ nhất của phương trình - {\log _{\sqrt 3 }}\left( {x - 2} ight).{\log _5}x = 2{\log _3}\left( {x - 2} ight) là?

    3 || ba || Ba

    Đáp án là:

    Nghiệm nguyên nhỏ nhất của phương trình - {\log _{\sqrt 3 }}\left( {x - 2} ight).{\log _5}x = 2{\log _3}\left( {x - 2} ight) là?

    3 || ba || Ba

    Điều kiện: x>2

    Ta có: - {\log _{\sqrt 3 }}\left( {x - 2} ight).{\log _5}x = 2{\log _3}\left( {x - 2} ight)

    \Leftrightarrow - 2{\log _3}\left( {x - 2} ight).{\log _5}x = 2{\log _3}\left( {x - 2} ight)

    \Leftrightarrow \left[ \begin{gathered} {\log _3}\left( {x - 2} ight) = 0 \hfill \\ {\log _5}x = - 1 \hfill \\ \end{gathered} ight. 

    \Leftrightarrow \left[ \begin{gathered} {\log _3}\left( {x - 2} ight) = 0 \hfill \\ {\log _5}x = - 1 \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = 3 \hfill \\ x = \frac{1}{5} \hfill \\ \end{gathered} ight.

    So điều kiện suy ra phương trình có nghiệm x=3.

  • Câu 11: Vận dụng
    Đếm số nghiệm thực

    Phương trình {\left( {\sqrt 3 - \sqrt 2 } ight)^x} + {\left( {\sqrt 3 + \sqrt 2 } ight)^x} = {\left( {\sqrt {10} } ight)^x} có tất cả bao nhiêu nghiệm thực ?

    Hướng dẫn:

     Ta có: {\left( {\sqrt 3 - \sqrt 2 } ight)^x} + {\left( {\sqrt 3 + \sqrt 2 } ight)^x} = {\left( {\sqrt {10} } ight)^x}\Leftrightarrow {\left( {\frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt {10} }}} ight)^x} + {\left( {\frac{{\sqrt 3 + \sqrt 2 }}{{\sqrt {10} }}} ight)^x} = 1

    Xét hàm số f\left( x ight) = {\left( {\frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt {10} }}} ight)^x} + {\left( {\frac{{\sqrt 3 + \sqrt 2 }}{{\sqrt {10} }}} ight)^x}

    Ta có: f\left( 2 ight) = 1

    Hàm số f (x) nghịch biến trên R do các cơ số \frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt {10} }} < 1;\frac{{\sqrt 3 + \sqrt 2 }}{{\sqrt {10} }} < 1.

    Vậy phương trình có nghiệm duy nhất là x=2.

  • Câu 12: Thông hiểu
    Tìm tập nghiệm của PT logarit

    Phương trình \log _2^2x - 4{\log _2}x + 3 = 0 có tập nghiệm là?

    Hướng dẫn:

    Điều kiện: x > 0

    \log _2^2x - 4{\log _2}x + 3 = 0 \Leftrightarrow \left[ \begin{gathered} {\log _2}x = 1 \hfill \\ {\log _2}x = 3 \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = 2 \hfill \\ x = 8 \hfill \\ \end{gathered} ight.

    Vậy PT có tập nghiệm là S={8;2}.

  • Câu 13: Vận dụng
    Đếm số nghiệm không âm

    Phương trình {3^{2x}} + 2x\left( {{3^x} + 1} ight) - {4.3^x} - 5 = 0 có tất cả bao nhiêu nghiệm không âm ?

    Hướng dẫn:

     Ta có: {3^{2x}} + 2x\left( {{3^x} + 1} ight) - {4.3^x} - 5 = 0 \Leftrightarrow \left( {{3^{2x}} - 1} ight) + 2x\left( {{3^x} + 1} ight) - \left( {{{4.3}^x} + 4} ight) = 0

    \Leftrightarrow \left( {{3^x} - 1} ight)\left( {{3^x} + 1} ight) + \left( {2x - 4} ight)\left( {{3^x} + 1} ight) = 0

    \Leftrightarrow \left( {{3^x} + 2x - 5} ight)\left( {{3^x} + 1} ight) = 0 \Leftrightarrow {3^x} + 2x - 5 = 0

    Xét hàm số f\left( x ight) = {3^x} + 2x - 5, ta có:f(1)=0.

    f'\left( x ight) = {3^x}\ln 3 + 2 > 0;\forall x \in \mathbb{R}. Do đó hàm số f(x) đồng biến trên R.

    Vậy nghiệm duy nhất của phương trình là x=1.

  • Câu 14: Thông hiểu
    Tìm tập nghiệm của PT

    Tập nghiệm của phương trình {\log _2}\frac{1}{x} = {\log _{\frac{1}{2}}}\left( {{x^2} - x - 1} ight) là:

    Hướng dẫn:

     Điều kiện: x > 0 và {x^2} - x - 1 > 0

    Với điều kiện đó thì {\log _2}\frac{1}{x} = {\log _{\frac{1}{2}}}x.

    Khi đó, phương trình đã cho tương đương phương trình:

    {\log _{\frac{1}{2}}}x = {\log _{\frac{1}{2}}}\left( {{x^2} - x - 1} ight) \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ x = {x^2} - x - 1 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ \left[ \begin{gathered} x = 1 + \sqrt 2 \hfill \\ x = 1 - \sqrt 2 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Leftrightarrow x = 1 + \sqrt 2

  • Câu 15: Nhận biết
    Số nghiệm của PT logarit

    Phương trình \log _2^2(x + 1) - 6{\log _2}\sqrt {x + 1} + 2 = 0 có số nghiệm là:

    2 || hai || 2 nghiệm || Hai nghiệm

    Đáp án là:

    Phương trình \log _2^2(x + 1) - 6{\log _2}\sqrt {x + 1} + 2 = 0 có số nghiệm là:

    2 || hai || 2 nghiệm || Hai nghiệm

     PT\Leftrightarrow \left\{ \begin{gathered} x + 1 > 0 \hfill \\ {\log ^2}_2(x + 1) - 3{\log _2}(x + 1) + 2 = 0 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} x > - 1 \hfill \\ \left[ \begin{gathered} {\log _2}(x + 1) = 1 \hfill \\ {\log _2}(x + 1) = 2 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > - 1 \hfill \\ \left[ \begin{gathered} x = 1 \hfill \\ x = 3 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ x = 3 \hfill \\ \end{gathered} ight.

    Vậy PT có 2 nghiệm.

  • Câu 16: Vận dụng cao
    Tìm m để PT vô nghiệm

    Với giá trị nào của tham số m thì phương trình {\left( {2 + \sqrt 3 } ight)^x} + {\left( {2 - \sqrt 3 } ight)^x} = m{\text{ }}vô nghiệm?

    m<2 || m nhỏ hơn 2

    Đáp án là:

    Với giá trị nào của tham số m thì phương trình {\left( {2 + \sqrt 3 } ight)^x} + {\left( {2 - \sqrt 3 } ight)^x} = m{\text{ }}vô nghiệm?

    m<2 || m nhỏ hơn 2

     Ta có nhận xét: \left( {2 + \sqrt 3 } ight)\left( {2 - \sqrt 3 } ight) = 1 \Leftrightarrow {\left( {2 + \sqrt 3 } ight)^x}{\left( {2 - \sqrt 3 } ight)^x} = 1.

    Đặt t = {\left( {2 + \sqrt 3 } ight)^x} \Rightarrow {\left( {2 - \sqrt 3 } ight)^x} = \frac{1}{t},\forall t \in \left( {0, + \infty } ight).

    Khi đó: \left( 1 ight) \Leftrightarrow t + \frac{1}{t} = m \Leftrightarrow f\left( t ight) = t + \frac{1}{t} = m{\text{ }}\left( {1'} ight),\forall t \in \left( {0, + \infty } ight).

    Xét hàm số f\left( t ight) = t + \frac{1}{t} xác định và liên tục trên \left( {0, + \infty } ight).

    Ta có: f'\left( t ight) = 1 - \frac{1}{{{t^2}}} = \frac{{{t^2} - 1}}{{{t^2}}}. Cho f'\left( t ight) = 0 \Leftrightarrow t = \pm 1.

    Bảng biến thiên:

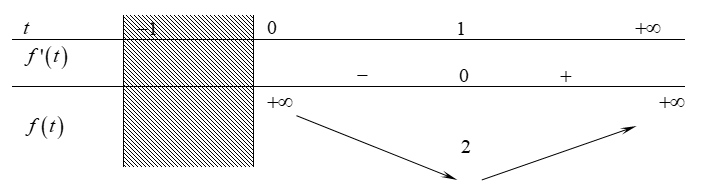
    Dựa vào bảng biến thiên:

    Phương trình (1') vô nghiệm khi và chỉ khi m < 2.

    Vậy Phương trình (1) vô nghiệm khi và chỉ khi Phương trình (1') vô nghiệm khi và chỉ khi m < 2.

  • Câu 17: Vận dụng cao
    Tính tổng các nghiệm

    Phương trình {3^{3 + 3x}} + {3^{3 - 3x}} + {3^{4 + x}} + {3^{4 - x}} = {10^3} có tổng các nghiệm là ?

    0 || không || Tổng các nghiệm bằng 0

    Đáp án là:

    Phương trình {3^{3 + 3x}} + {3^{3 - 3x}} + {3^{4 + x}} + {3^{4 - x}} = {10^3} có tổng các nghiệm là ?

    0 || không || Tổng các nghiệm bằng 0

    Ta có: {3^{3 + 3x}} + {3^{3 - 3x}} + {3^{4 + x}} + {3^{4 - x}} = {10^3} (*)

    Khi đó: \left( * ight) \Leftrightarrow {27.3^{3x}} + \frac{{27}}{{{3^{3x}}}} + {81.3^x} + \frac{{81}}{{{3^x}}} = {10^3}

    \Leftrightarrow 27.\left( {{3^{3x}} + \frac{1}{{{3^{3x}}}}} ight) + 81.\left( {{3^x} + \frac{1}{{{3^x}}}} ight) = {10^3}{\text{ }}\left( {**} ight)

    Đặt t = {3^x} + \frac{1}{{{3^x}}}\mathop \geqslant \limits^{Cauchy} 2\sqrt {{3^x}.\frac{1}{{{3^x}}}} = 2 (Áp dụng theo BĐT Cauchy cho 2 số không âm).

    \Rightarrow {t^3} = {\left( {{3^x} + \frac{1}{{{3^x}}}} ight)^3} = {3^{3x}} + {3.3^{2x}}.\frac{1}{{{3^x}}} + {3.3^x}.\frac{1}{{{3^{2x}}}} + \frac{1}{{{3^{3x}}}}

    \Leftrightarrow {3^{3x}} + \frac{1}{{{3^{3x}}}} = {t^3} - 3t

    Khi đó: \left( {**} ight) \Leftrightarrow 27\left( {{t^3} - 3t} ight) + 81t = {10^3} \Leftrightarrow {t^3} = \frac{{{{10}^3}}}{{27}} \Leftrightarrow t = \frac{{10}}{3} > 2{\text{ }}

    Với t = \frac{{10}}{3} \Rightarrow {3^x} + \frac{1}{{{3^x}}} = \frac{{10}}{3}{\text{ }}\left( {***} ight)

    Đặt y = {3^x} > 0. Khi đó: \left( {***} ight) \Leftrightarrow y + \frac{1}{y} = \frac{{10}}{3} \Leftrightarrow 3{y^2} - 10y + 3 = 0 \Leftrightarrow \left[ \begin{gathered} y = 3{\text{ }} \hfill \\ y = \frac{1}{3}{\text{ }} \hfill \\ \end{gathered} ight.

    Với y = 3 \Rightarrow {3^x} = 3 \Leftrightarrow \boxed{x = 1}

    Với y = \frac{1}{3} \Rightarrow {3^x} = \frac{1}{3} \Leftrightarrow \boxed{x = - 1}.

  • Câu 18: Thông hiểu
    Điều kiện xác định

    Điều kiện xác định của phương trình \log ({x^2} - 6x + 7) + x - 5 = \log (x - 3) là:

    Hướng dẫn:

    Điều kiện phương trình xác định:  

    \left\{ \begin{gathered} {x^2} - 6{\text{x + 7}} > 0 \hfill \\ x - 3 > 0 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} x > 3 + \sqrt 2 \hfill \\ x < 3 - \sqrt 2 \hfill \\ \end{gathered} ight. \hfill \\ x > 3 \hfill \\ \end{gathered} ight. \Leftrightarrow x > 3 + \sqrt 2

  • Câu 19: Nhận biết
    Tìm tập nghiệm PT Logarit

    Phương trình \log _2^{}x + {\log _2}(x - 1) = 1 có tập nghiệm là:

    {2} || T={2}

    Đáp án là:

    Phương trình \log _2^{}x + {\log _2}(x - 1) = 1 có tập nghiệm là:

    {2} || T={2}

     PT \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ x - 1 > 0 \hfill \\ {\log _2}\left[ {x(x - 1)} ight] = 1 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} x > 1 \hfill \\ {x^2} - x - 2 = 0 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > 1 \hfill \\ \left[ \begin{gathered} x = - 1 \hfill \\ x = 2 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Leftrightarrow x = 2.

  • Câu 20: Nhận biết
    Đếm số nghiệm

    Số nghiệm của phương trình {\log _2}({x^3} + 1) - {\log _2}({x^2} - x + 1) - 2{\log _2}x = 0 là:

    0 || PT không có nghiệm || không có nghiệm || vô nghiệm || PT vô nghiệm

    Đáp án là:

    Số nghiệm của phương trình {\log _2}({x^3} + 1) - {\log _2}({x^2} - x + 1) - 2{\log _2}x = 0 là:

    0 || PT không có nghiệm || không có nghiệm || vô nghiệm || PT vô nghiệm

     PT \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ {x^3} + 1 > 0 \hfill \\ {x^2} - x + 1 > 0 \hfill \\ {\log _{{2^{}}}}({x^3} + 1) - {\log _2}({x^2} - x + 1) - 2{\log _{{2^{}}}}x = 0 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ \frac{{{x^3} + 1}}{{{x^2}({x^2} - x + 1)}} = 0 \hfill \\ \end{gathered} ight.  \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ \frac{{(x + 1)({x^2} - x + 1)}}{{{x^2}({x^2} - x + 1)}} = 0 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ x + 1 = 0 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ x = - 1 \hfill \\ \end{gathered} ight. \Rightarrow x \in \emptyset

    Vậy số nghiệm của PT là 0.

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (30%):
    2/3
  • Thông hiểu (30%):
    2/3
  • Vận dụng (30%):
    2/3
  • Vận dụng cao (10%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 2 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 12

Đăng nhập