Lớp 11 Toán 11 - Chân trời sáng tạo

Giá trị lượng giác của một góc lượng giác CTST

1. Giá trị lượng giác của góc lượng giác

Định nghĩa: Giả sử điểm M\left( {x;y} \right) là điểm trên đường tròn lượng giác, biểu diễn góc lượng giác có số đo \alpha (như hình vẽ):

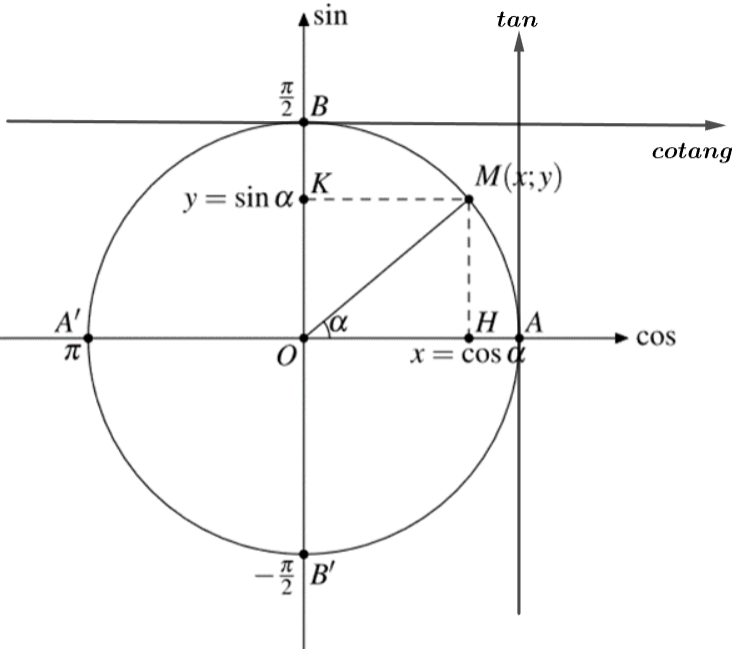
Giá trị lượng giác của một góc lượng giác CTST

  • Hoành độ x = \cos \alpha
  • Tung độ y = \sin \alpha
  • \tan \alpha = \frac{y}{x} = \frac{{\sin \alpha }}{{\cos \alpha }};\left( {x \ne 0} \right) hay \tan \alpha xác định khi \alpha \ne \frac{\pi }{2} + k\pi ;\left( {k \in \mathbb{Z}} \right)
  • \cot \alpha = \frac{x}{y} = \frac{{\cos \alpha }}{{\sin \alpha }};\left( {y \ne 0} \right) hay \cot \alpha xác định khi \alpha \ne k\pi ;\left( {k \in \mathbb{Z}} \right)

Chú ý:

 + Trục tung là trục sin, trục hoành là trục cosin.

+ Trục có gốc tại điểm A(1; 0) song song với trục sin là trục tang.

+ Trục có gốc tại điểm B(0; 1) song song với trục cosin là trục cotang.

a) Một số chú ý quan trọng

Với mọi góc lượng giác α và số nguyên k ta có:

\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \cos \left( {\alpha + k2\pi } \right) = \cos \alpha
\tan \left( {\alpha + k\pi } \right) = \tan \alpha \cot \left( {\alpha + k\pi } \right) = \cot \alpha

Chú ý: Dấu của các giá trị lượng giác của một góc lượng giác phụ thuộc vào vị trí điểm biểu diễn M trên đường tròn lượng giác.

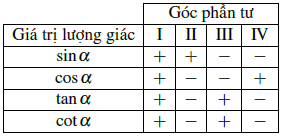
Giá trị lượng giác của một góc lượng giác CTST

b) Giá trị lượng giác của các góc đặc biệt

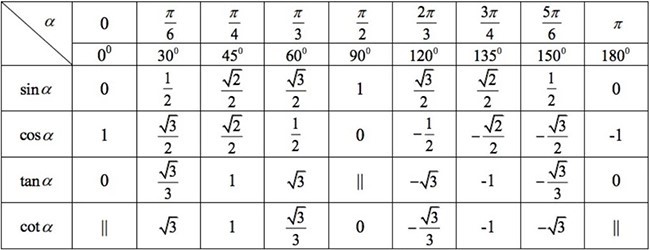
Giá trị lượng giác của một góc lượng giác CTST

Biểu diễn trên vòng tròn lượng giác

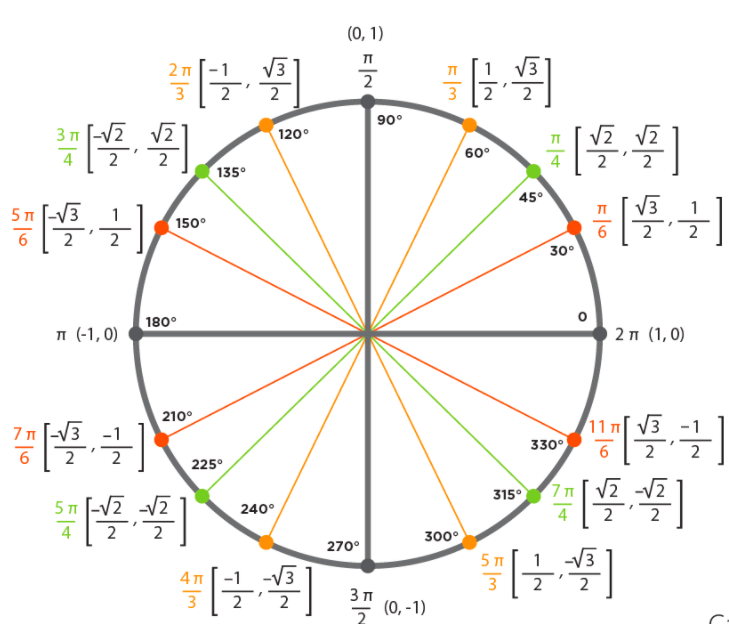
Giá trị lượng giác của một góc lượng giác CTST

Ví dụ: Cho góc {0^0} < \alpha < {90^0}. Xét dấu biểu thức: A = \sin \left( {\alpha + {{90}^0}} \right) và B = \cos \left( {{{270}^0} - \alpha } \right)?

Hướng dẫn giải

A = \sin \left( {\alpha + {{90}^0}} \right)

Ta có: {0^0} < \alpha < {90^0} \Rightarrow {90^0} < \alpha + {90^0} < {180^0}

\Rightarrow A = \sin \left( {\alpha + {{90}^0}} \right) > 0

B = \cos \left( {{{270}^0} - \alpha } \right)

Ta có:

{0^0} < \alpha < {90^0} \Rightarrow {180^0} < {270^0} - \alpha < {270^0}

\Rightarrow \cos \left( {{{270}^0} - \alpha } \right) < 0

Câu trắc nghiệm mã số: 44627,44573

2. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác

{\sin ^2}\alpha + {\cos ^2}\alpha = 1 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }};\left( {\alpha \ne \frac{\pi }{2} + k\pi ;k \in \mathbb{Z}} \right)
1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }};\left( {\alpha \ne k\pi ;k \in \mathbb{Z}} \right) \tan \alpha .\cot \alpha = 1;\left( {\alpha \ne \frac{{k\pi }}{2};k \in \mathbb{Z}} \right)

Ví dụ: Rút gọn biểu thức: B = {\left( {\frac{{\sin x + \tan x}}{{\cos x + 1}}} \right)^2} + 1

Hướng dẫn giải

Ta có:

B = {\left( {\frac{{\sin x + \tan x}}{{\cos x + 1}}} \right)^2} + 1

B = {\left( {\dfrac{{\sin x + \dfrac{{\sin x}}{{\cos x}}}}{{\cos x + 1}}} \right)^2} + 1

B = {\left[ {\frac{{\sin x\left( {\cos x + 1} \right)}}{{\cos x\left( {\cos x + 1} \right)}}} \right]^2} + 1

B = {\left( {\frac{{\sin x}}{{\cos x}}} \right)^2} + 1 = {\tan ^2}x + 1 = \frac{1}{{{{\cos }^2}x}}

Câu trắc nghiệm mã số: 33358,32852

3. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt

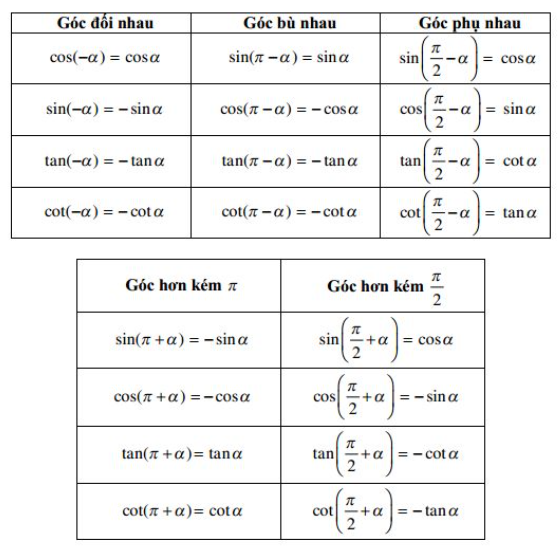
Giá trị lượng giác của một góc lượng giác CTST

Ví dụ: Rút gọn biểu thức: A = \cos \left( {3\pi + x} \right) + \cos \left( {2\pi - x} \right) + \cos \left( {\frac{\pi }{2} + x} \right)

Hướng dẫn giải

Ta có:

A = \cos \left( {3\pi + x} \right) + \cos \left( {2\pi - x} \right) + \cos \left( {\frac{\pi }{2} + x} \right)

A = - \cos x + \cos \left( { - x} \right) - \sin x

A = - \cos x + \cos x - \sin x

A = - \sin x

Câu trắc nghiệm mã số: 44581
  • 54 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CTST