Cho tứ diện O.ABC trong đó ba đường thẳng OB, OC, OA đôi một vuông góc. Trong các mệnh đề sau, mệnh đề nào sai?
Tam giác ABC luôn là tam giác nhọn
Cho tứ diện O.ABC trong đó ba đường thẳng OB, OC, OA đôi một vuông góc. Trong các mệnh đề sau, mệnh đề nào sai?

Tam giác ABC luôn là tam giác nhọn
Góc giữa hai đường thẳng bất kì trong không gian là góc nào trong các góc dưới đây?
Góc giữa hai đường thẳng m và n trong không gian, kí hiệu là (m, n) là góc giữa hai đường thẳng a và b cùng đi qua một điểm và tương ứng song song với m và n.
Cho tứ diện đều ABCD có I và J lần lượt là trung điểm của AB và CD. Tính cosin góc giữa hai cạnh AJ và CI?
Hình vẽ minh họa:
Giả sử cạnh tứ diện đều bằng a. Khi đó:
Ta có:
Vậy cosin góc giữa hai cạnh AJ và CI bằng
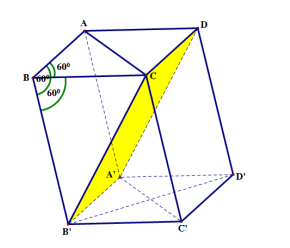
Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh bằng a (hình hộp như thế gọi là hình hộp thoi) và ![]() . Tính diện tích tứ giác A’B’CD.
. Tính diện tích tứ giác A’B’CD.
Hình vẽ minh họa:
Ta có:
=> A’B’ // CD và A’B’ = CD
=> Tứ giác A’B’CD là hình bình hành
Ngoài ra B’C = a = CD
=> => Tứ giác A’B’CD là hình thoi
Ta sẽ chứng minh tứ giác A’B’CD là hình vuông.
Ta có:
=> Tứ giác A’B’CD là hình vuông.
Diện tích hình vuông đó là a2
Trong không gian cho hai tam giác đều ABC và ABC’ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, CB, BC’ và C’A. Tứ giác MNPQ là hình gì?
Hình vẽ minh họa:
Vì M, N, P, Q lần lượt là trung điểm của các cạnh AC, CB, BC’ và C’A
=>
=> MNPQ là hình bình hành
Gọi H là trung điểm của AB
Vì hai tam giác ABC và ABC’ đều nên
=>
Ta có:
Vậy tứ giác MNPQ là hình chữ nhật
Cho hình hộp ABCD.A’B’C’D’. Giả sử tam giác AB’C và A’DC’ đều có ba góc nhọn. Góc giữa hai đường thẳng AC, A’D là góc nào sau đây?
Do ACC’A’ là hình bình hành nên AC song song với A’C’. Do đó:
Như vậy
Cho tứ diện ABCD có SC = AC = AB = ![]() , SC ⊥ (ABC), tam giác ABC vuông tạo A, các điểm M thuộc SA, N thuộc BCc sao cho AM = CN = t (0 < t < 2a). Tìm t để MN ngắn nhất.
, SC ⊥ (ABC), tam giác ABC vuông tạo A, các điểm M thuộc SA, N thuộc BCc sao cho AM = CN = t (0 < t < 2a). Tìm t để MN ngắn nhất.
Hình vẽ minh họa:
Theo giả thiết, ta có: SA = 2a, BC = 2a
Vì 0 < t < 2a
Đặt . Ta có:
Vậy
Từ đó suy ra MN nhỏ nhất khi và chỉ khi
Cho tứ diện đều ABCD, M là trung điểm của CD, N là điểm nằm trên AD sao cho BN vuông góc với AM. Tính tỉ số ![]()
Hình vẽ minh họa:
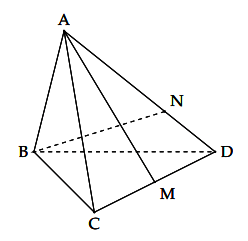
Đặt . Ta có:
Giả sử AN = k.AD. Khi đó:
Vì M là trung điểm của CD nên
Khi đó: BN ⊥ AM =>
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm của SC. Tính cosin góc giữa hai đường thẳng BM và AC.
Hình vẽ minh họa:
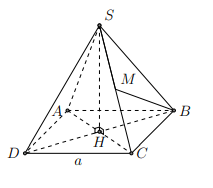
Gọi H là tâm của hình vuông ABCD khi đó
Ta có:
Vì tam giác SBC đều cạnh a và BM là trung tuyến nên
Khi đó:
Cho tứ diện ABCD có AC = a, BD = 3a. Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN.
Hình vẽ minh họa:
Gọi P là trung điểm của AB => PN, PM lần lượt là đường trung bình của tam giác ABC và tam giác ABD.
=>
Ta có:
=>
Cho hình hộp ABCD.A’B’C’D có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau. Mệnh đề nào có thể sai?
Dễ thấy các đáp án A’C’ ⊥ BD, A’B ⊥ DC’, BC’ ⊥ A’D đúng
Đáp án BB’ ⊥ BD sẽ bị sai trong trường hợp hình hộp có cạnh bên không vuông góc với mặt đáy
Cho tứ diện ABCD có ![]() . Gọi α là góc giữa AB và CD. Chọn khẳng định đúng?
. Gọi α là góc giữa AB và CD. Chọn khẳng định đúng?
Hình vẽ minh họa:
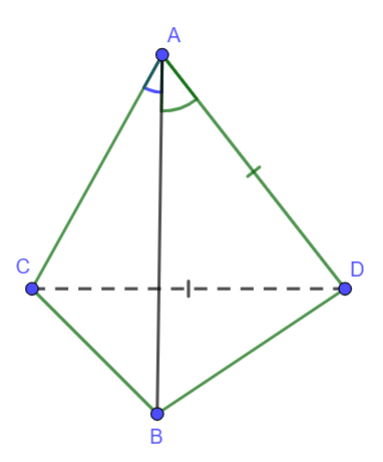
Ta có:
Mặt khác:
Trong không gian cho đường thẳng a và điểm M. Có bao nhiêu đường thẳng đi qua M, cắt a và vuông góc với a?
Có 1 nếu M không thuộc a, có vô số nếu M thuộc a
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo góc (IJ; CD) bằng:
Hình vẽ minh họa:
Gọi O là tâm của hình thoi ABCD
=> OJ là đường trung bình của tam giác BCD =>
Vì CD // OJ => (IJ; CD) = (IJ; OJ)
Xét tam giác IOJ có: => Tam giác IOJ đều
Vậy (IJ; CD) = (IJ; OJ) =
Cho tứ diện ABCD có BD vuông góc với AB và CD. Gọi P và Q lần lượt là trung điểm của các cạnh CD và AB thỏa mãn BD : CD : PQ : AB = 3 : 4 : 5 : 6. Gọi ψ là góc giữa hai đường thẳng AB và CD. Tính giá trị của cosψ
Hình vẽ minh họa:
Do AB vuông góc với BD nên AB nằm trong mặt phẳng (α) chứa AB và vuông góc với BD. Dựng hình chữ nhật BDPR thì góc giữa hai đường thẳng AB và CD cũng là góc giữa hai đường thẳng AB và BR. Ta có:
