Lớp 11 Toán 11 - Chân trời sáng tạo

Khoảng cách trong không gian CTST

1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng

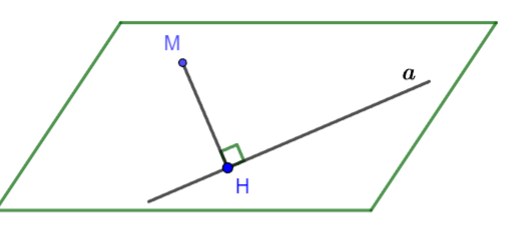
Nếu H là hình chiếu vuông góc của điểm M trên đường thẳng a thì độ dài đoạn MH được gọi là khoảng cách từ M đến đường thẳng a. Kí hiệu d(M, a).

Hình vẽ minh họa

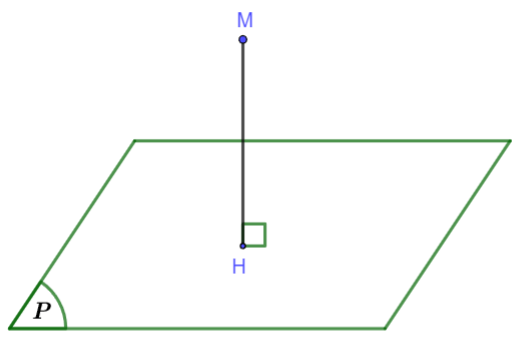
Khoảng cách trong không gian CTST

Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dài đoạn MH được gọi là khoảng cách từ M đến (P). Kí hiệu: d(M, (P)).

Hình vẽ minh họa

Khoảng cách trong không gian CTST

Quy ước:

  • d\left( {M,a} \right) = 0 \Leftrightarrow M \in a
  • d\left( {M,\left( P \right)} \right) = 0 \Leftrightarrow M \in \left( P \right)

Nhận xét:

a) Lấy điểm N tùy ý trên đường thẳng a ta luôn có d\left( {M,a} \right) \leqslant MN.

b) Lấy điểm N tùy ý trên mặt phẳng (P) ta luôn có d\left( {M,\left( P \right)} \right) \leqslant MN.

2. Khoảng cách giữa các đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song

  • Khoảng cách giữa hai đường thẳng song song a và b là khoảng cách từ một điểm bất kì trên a đến b, kí hiệu d(a, b).
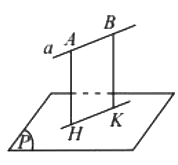
  • Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P), kí hiệu d(a, (P)).

Hình vẽ minh họa

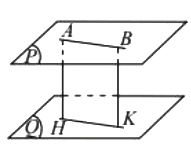
Khoảng cách trong không gian CTST

Khoảng cách giữa hai mặt phẳng song song (P) và (Q) là khoảng cách từ một điểm bất kì trên (P) đến (Q). Kí hiệu d((P), (Q)).

Hình vẽ minh họa

Khoảng cách trong không gian CTST

3. Khoảng cách giữa hai đường thẳng chéo nhau

  • Đường thẳng c vừa vuông góc, vừa cắt hai đường thẳng chéo nhau a và b được gọi là đường vuông góc chung của a và b.
  • Nếu đường vuông góc chung của hai đường thẳng chéo nhau a và b cắt chúng lần lượt tại I và J thì đoạn IJ là đoạn vuông góc chung của a và b.

Hình vẽ minh họa

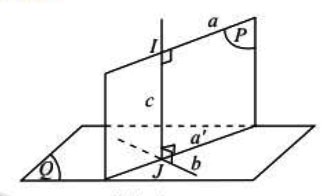
Khoảng cách trong không gian CTST

Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó. Kí hiệu d(a, b).

Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, góc ABC bằng 600, biết tam giác SBC đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính theo a khoảng cách:

a) Từ điểm S đến mặt phẳng (ABC).

b) Từ điểm B đến mặt phẳng (SAC).

c) Giữa hai đường thẳng AB và SC.

Hướng dẫn giải

Hình vẽ minh họa

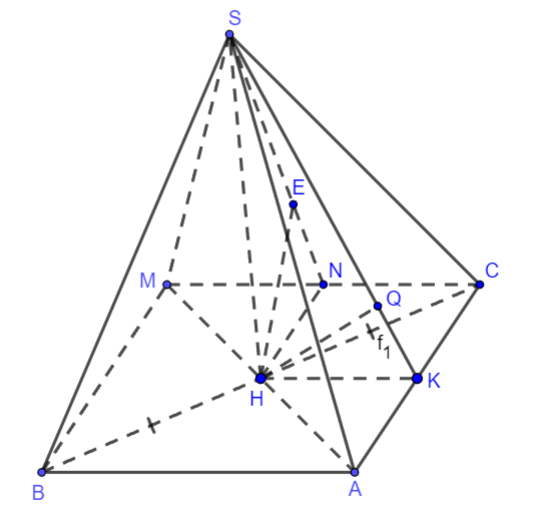
Khoảng cách trong không gian CTST

a) Kẻ SH vuông góc với BC tại H thì SH ⊥ (ABC) suy ra d\left( {S,\left( {ABC} \right)} \right) = SH = \frac{{a\sqrt 3 }}{2}

b) Kẻ HK vuông góc với AC tại K, HQ vuông góc với SK tại Q thì d\left( {H,\left( {SAC} \right)} \right) = HQ

Ta có: AB = \frac{a}{2},HK = \frac{a}{4} và tam giác SHK vuông tại H, đường cao HQ nên HQ = \frac{{SH.HK}}{{SK}} = \frac{{a\sqrt {39} }}{{26}}

Lại có H là trung điểm của BC nên d\left( {B,\left( {SAC} \right)} \right) = 2d\left( {H,\left( {SAC} \right)} \right) = \frac{{a\sqrt {39} }}{{13}}

c) Dựng hình bình hành ABMC, chứng minh được ABMC là hình chữ nhật.

Khi đó AB//(SCM) và mặt phẳng (SMC) chứa SC nên d(AB, SC)= d(AB,( SCM)= d(B,(SCM))=2d(H; (SCM))

Kẻ HN vuông góc với CM tại N, HE vuông góc với SN tại N thì HE ⊥(SCM) suy ra d(H; (SCM)= HE

Ta có: HN = \frac{{BM}}{2} = \frac{{a\sqrt 3 }}{4} tam giác SHN vuông tại H, đường cao HE nên HE = \frac{{SH.HN}}{{SN}} = \frac{{a\sqrt {15} }}{{10}}

Vậy d\left( {AB,BC} \right) = \frac{{a\sqrt {15} }}{5}

Chú ý:

a) Khoảng cách giữa hai đường thẳng chéo nhau a và b bằng khoảng cách giữa một trong hai đường đến mặt phẳng song song với nó và chứa đường còn lại.

b) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.

Câu trắc nghiệm mã số: 12695

4. Công thức tính thể tích của khối chóp, khối lăng trụ, khối hộp

Thể tích

Phát biểu

Minh họa

Công thức

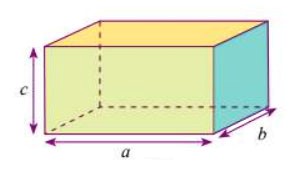
Khối hộp chữ nhật

Bằng diện tích đáy nhân với chiều cao

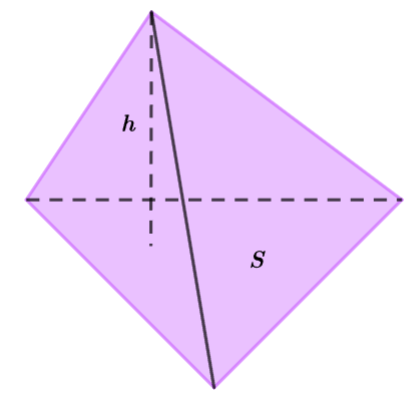
 Khoảng cách trong không gian CTST  V = a.b.c

Khối chóp

Bằng một phần ba diện tích đáy nhân với chiều cao

 Khoảng cách trong không gian CTST V = \frac{1}{3}.S.h

Khối lăng trụ

Bằng diện tích đáy nhân với chiều cao

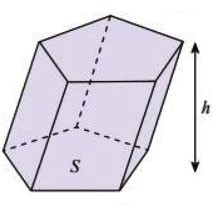 Khoảng cách trong không gian CTST V = S.h

Khối chóp cụt đều

 

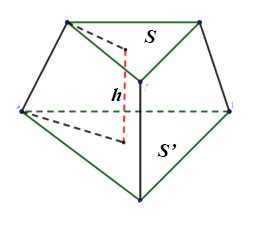 Khoảng cách trong không gian CTST V = \frac{1}{3}.h.\left( {S + S' + \sqrt {S.S'} } \right)

Ví dụ: Một hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước là 2cm, 3cm, 6 cm. Tính thể tích của khối tứ diện ACB’D’.

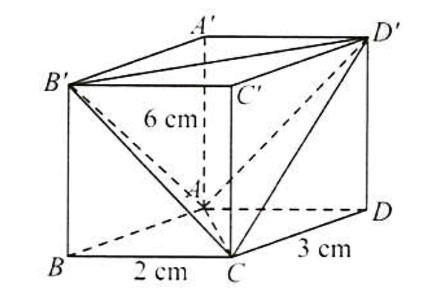
Khoảng cách trong không gian CTST

Hướng dẫn giải

Ta có:

\begin{matrix} {V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}} = {V_{BA{B^\prime }C}} + {V_{DAC{D^\prime }}} + {V_{A{B^\prime }A{D^\prime }}} + {V_{{C^\prime }{B^\prime }C{D^\prime }}} + {V_{AC{B^\prime }{D^\prime }}} \hfill \\ = 4{V_{BA{B^\prime }{C^\prime }}} + {V_{AC{B^\prime }{D^\prime }}} \hfill \\ \Rightarrow {V_{AC{B^\prime }D}} = {V_{ABCD{A^\prime }{B^\prime }{C^\prime }{D^\prime }}} - 4{V_{BA{B^\prime }C}} \hfill \\ = {V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}} - 4 \cdot \dfrac{1}{6}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}} \hfill \\ = \dfrac{1}{3}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}} = \dfrac{1}{3}.2.3.6 = 12\left( {c{m^3}} \right) \hfill \\ \end{matrix}

Chú ý: Khối lăng trụ có cạnh bên vuông góc với đáy là khối lăng trụ đứng. Chiều dài cạnh bên a của khối lăng trụ đứng bằng chiều cao h và ta có công thức V = S.a

Hình vẽ minh họa

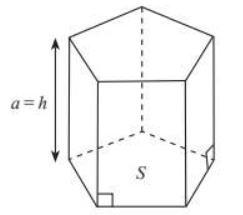
Khoảng cách trong không gian CTST

Ví dụ: Cho hình chóp cụt tam giác đều ABC.A’B’C’ có đường cao HH’ = 3a. Biết AB=2a, A’B’=a. Tính thể tích hình chóp cụt ABC.A’B’C’.

Hướng dẫn giải

Hình vẽ minh họa

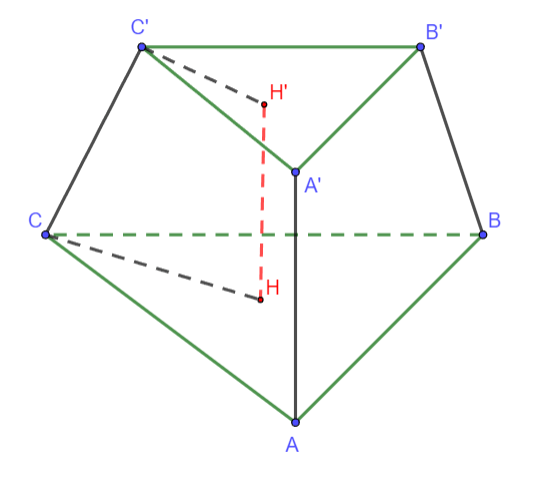
Khoảng cách trong không gian CTST

Áp dụng công thức V = \frac{1}{3}.h.\left( {S + S' + \sqrt {S.S'} } \right)

Với \left\{ \begin{gathered} S = {a^2}.\sqrt 3 \hfill \\ S' = \frac{{{a^2}.\sqrt 3 }}{4} \hfill \\ h = 3a \hfill \\ \end{gathered} \right., khi đó:

V = \frac{1}{3}.3a.\left( {{a^2}\sqrt 3 + \frac{{{a^2}\sqrt 3 }}{4} + \sqrt {{a^2}\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4}} } \right)

= \frac{{7{a^3}\sqrt 3 }}{4}

Câu trắc nghiệm mã số: 43402,43318,43316
  • 1 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CTST