Lớp 11 Toán 11 - Chân trời sáng tạo

Hàm số lượng giác và đồ thị CTST

1. Hàm số lượng giác

Loại

Định nghĩa

Kí hiệu

Tập xác định

Hàm số sin

quy tắc đặt tương ứng với mỗi số thực x với số thực sinx

y = \sin x

\mathbb{R}

Hàm số cosin

quy tắc đặt tương ứng với mỗi số thực x với số thực cosx

y = \cos x

\mathbb{R}

Hàm số tang

được cho bằng công thức  y = \frac{{\sin x}}{{\cos x}}

y = \tan x

\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}

Hàm số cotang

được cho bằng công thức y = \frac{{\cos x}}{{\sin x}}

y = \cot x

\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}

Ví dụ: Tìm tập xác định của hàm số:

a. y = \frac{{1 - 2{x^2}}}{{1 - \cos 2x}}

b. y = \sqrt {2 - 2\sin x}

c. y = \tan \left( {x + \frac{\pi }{4}} \right)

d. y = \cot \left( {\frac{\pi }{4} - 2x} \right) - \frac{2}{{1 - \cos x}}

Hướng dẫn giải

a) Hàm số y = \frac{{1 - 2{x^2}}}{{1 - \cos 2x}} xác định khi và chỉ khi

\begin{matrix} 1 - \cos 2x \ne 0 \Leftrightarrow \cos 2x \ne 1 \hfill \\ \Leftrightarrow 2x \ne k2\pi \Leftrightarrow x \ne k\pi ;\left( {k \in \mathbb{Z}} \right) \hfill \\ \end{matrix}

Vậy tập xác định của hàm số D = \mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}

b) Hàm số y = \sqrt {2 - 2\sin x} xác định khi và chỉ khi

2 - 2\sin x \geqslant 0 \Leftrightarrow \sin x \leqslant 1 luôn đúng với \forall x \in \mathbb{R}

Vậy tập xác định của hàm số D = \mathbb{R}.

c) Hàm số y = \tan \left( {x + \frac{\pi }{4}} \right) xác định khi và chỉ khi

\begin{matrix} \cos \left( {x + \dfrac{\pi }{4}} \right) \ne 0 \hfill \\ \Leftrightarrow x + \dfrac{\pi }{4} \ne \dfrac{\pi }{2} + k\pi ;\left( {k \in \mathbb{Z}} \right) \hfill \\ \Leftrightarrow x \ne \dfrac{\pi }{4} + k\pi ;\left( {k \in \mathbb{Z}} \right) \hfill \\ \end{matrix}

Vậy tập xác định của hàm số D = \mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\pi |k \in \mathbb{Z}} \right\}.

d) Hàm số y = \cot \left( {\frac{\pi }{4} - 2x} \right) - \frac{2}{{1 - \cos x}} xác định khi và chỉ khi

\begin{matrix} \left\{ \begin{gathered} \sin \left( {\dfrac{\pi }{4} - 2x} \right) \ne 0 \hfill \\ 1 - \cos x \ne 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} \dfrac{\pi }{4} - 2x \ne k\pi \hfill \\ \cos x \ne 1 \hfill \\ \end{gathered} \right. \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \ne \dfrac{\pi }{8} - \dfrac{{k\pi }}{2} \hfill \\ x \ne k2\pi \hfill \\ \end{gathered} \right.;\left( {k \in \mathbb{Z}} \right) \hfill \\ \end{matrix}

Vậy tập xác định của hàm số D = \mathbb{R}\backslash \left\{ {\frac{\pi }{8} - \frac{{k\pi }}{2};k2\pi |k \in \mathbb{Z}} \right\}.

2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

a) Hàm số chẵn, hàm số lẻ

Cho hàm số y=f(x) có tập xác định D.

  • Hàm số f\left( x \right) được gọi là hàm số chẵn nếu \forall x \in D thì \left\{ \begin{gathered} - x \in D \hfill \\ f\left( { - x} \right) = f\left( x \right) \hfill \\ \end{gathered} \right.
  • Hàm số f\left( x \right) được gọi là hàm số lẻ nếu \forall x \in D thì \left\{ \begin{gathered} - x \in D \hfill \\ f\left( { - x} \right) = - f\left( x \right) \hfill \\ \end{gathered} \right.

Chú ý:

  • Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.
  • Đồ thị của một hàm số lẻ nhận trục hoành làm trục đối xứng.

Ví dụ: Xét tính chẵn lẻ của các hàm số sau:

a) y = 2x.\sin x

b) y = \cos x + \sin 2x

c) y = \frac{{\cos 2x}}{x}

Hướng dẫn giải

a) Tập xác định D = \mathbb{R} là tập đối xứng do đó \forall x \in D \Rightarrow - x \in D\left( * \right)

Đặt y = f\left( x \right) = 2x.\sin x

Với \forall x \in D ta có:

f\left( { - x} \right) = 2\left( { - x} \right).\sin \left( { - x} \right) = 2x.\sin x = f\left( x \right)\left( {**} \right)

Từ (*) và (**) suy ra hàm số đã cho là hàm số chẵn.

b) Tập xác định D = \mathbb{R} là tập đối xứng

Đặt y = f\left( x \right) = \cos x + \sin 2x

Xét x = \frac{\pi }{3} \in D \Rightarrow x = - \frac{\pi }{3} \in D

\begin{matrix} f\left( {\dfrac{\pi }{3}} \right) = \cos \left( {\dfrac{\pi }{3}} \right) + \sin \left( {\dfrac{{2\pi }}{3}} \right) = \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2} \hfill \\ f\left( { - \dfrac{\pi }{3}} \right) = \cos \left( { - \dfrac{\pi }{3}} \right) + \sin \left( { - \dfrac{{2\pi }}{3}} \right) = \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2} \hfill \\ \end{matrix}

Ta thấy f\left( {\frac{\pi }{3}} \right) \ne f\left( { - \frac{\pi }{3}} \right) nên hàm số đã cho không là hàm số chẵn.

f\left( {\frac{\pi }{3}} \right) \ne - f\left( { - \frac{\pi }{3}} \right) nên hàm số đã cho không là hàm số lẻ.

Vậy hàm số đã cho không chẵn, không lẻ.

c) Tập xác định D = \mathbb{R}\backslash \left\{ 0 \right\} là tập đối xứng do đó \forall x \in D \Rightarrow - x \in D\left( * \right)

Đặt f\left( x \right) = \frac{{\cos 2x}}{x}

Với \forall x \in D ta có:

.f\left( { - x} \right) = \frac{{\cos \left( { - 2x} \right)}}{{ - x}} = - \frac{{\cos \left( {2x} \right)}}{x} = - f\left( x \right)\left( {**} \right)

Từ (*) và (**) suy ra hàm số đã cho là hàm số lẻ.

Câu trắc nghiệm mã số: 44585,2519

b) Hàm số tuần hoàn

Định nghĩa: Hàm số có tập xác định được gọi là hàm số tuần hoàn, nếu tồn tại một số T \ne 0 sao cho với mọi x \in D ta có:

  • \left\{ {\begin{array}{*{20}{c}} {x - T \in D} \\ {x + T \in D} \end{array}} \right.
  • f\left( {x + T} \right) = f\left( x \right)

Số dương T nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó.

Nhận xét:

  • y = \sin x tuần hoàn với chu kì T = 2\pi
  • y = \cos x tuần hoàn với chu kì T = 2\pi
  • y = \tan x tuần hoàn với chu kì T = \pi
  • y = \cot x tuần hoàn với chu kì T = \pi

Công thức mở rộng

  • Hàm số y = \sin \left( {ax + b} \right) tuần hoàn với chu kì T = \frac{{2\pi }}{{\left| a \right|}}
  • Hàm số y = \cos \left( {ax + b} \right) tuần hoàn với chu kì T = \frac{{2\pi }}{{\left| a \right|}}
  • Hàm số y = \tan \left( {ax + b} \right) tuần hoàn với chu kì T = \frac{{\pi }}{{\left| a \right|}}
  • Hàm số y = \cot \left( {ax + b} \right) tuần hoàn với chu kì T = \frac{{\pi }}{{\left| a \right|}}

Ví dụ: Xét tính tuần hoàn và chu kì cơ sở của các hàm số sau:

a. y = 1 - \sin 5x

b. y = {\cos ^2}x - 1

c. y = \sin \left( {\frac{{2x}}{5}} \right).\cos \left( {\frac{{2x}}{5}} \right)

d. y = \cos x + \cos \left( {\sqrt 3 x} \right)

Hướng dẫn giải

a) Hàm số y = 1 - \sin 5x tuần hoàn với chu kì T = \frac{{2\pi }}{5}

b) Hàm số y = {\cos ^2}x - 1 = \frac{{\cos 2x - 1}}{2} tuần hoàn với chu kì T = \pi

a) Ta có: y = \sin \left( {\frac{{2x}}{5}} \right).\cos \left( {\frac{{2x}}{5}} \right) = \frac{1}{2}\sin \left( {\frac{{4x}}{5}} \right)

Hàm số tuần hoàn với chu kì

d) Hàm số y = \cos x + \cos \left( {\sqrt 3 x} \right) không tuần hoàn.

Vì ta có hàm số y = \cos x tuần hoàn với chu kì {T_1} = 2\pi và hàm số y = \cos \left( {\sqrt 3 x} \right) tuần hoàn với chu kì {T_2} = \frac{{2\pi }}{{\sqrt 3 }} nhưng không tồn tại bội chung nhỏ nhất của {T_1} = 2\pi và {T_2} = \frac{{2\pi }}{{\sqrt 3 }}.

Câu trắc nghiệm mã số: 8766

3. Đồ thị của các hàm số lượng giác

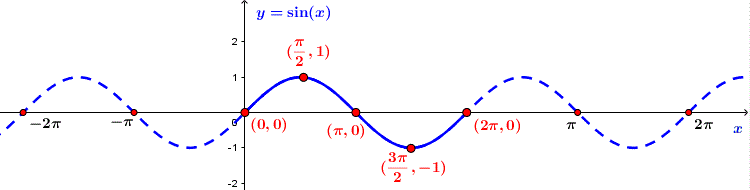
a) Hàm số y = sinx

- Tập xác định: D = \mathbb{R}

- Tập giá trị [-1; 1] hay - 1 \leqslant \operatorname{sinx} \leqslant 1,\forall x \in \mathbb{R}

- Hàm số là hàm số lẻ tuần hoàn với chu kì T = 2\pi

- Đồng biến trên mỗi khoảng \left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right) và nghịch biến trên mỗi khoảng \left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right), k \in \mathbb{Z}

- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.

Đồ thị hàm số y = \sin x

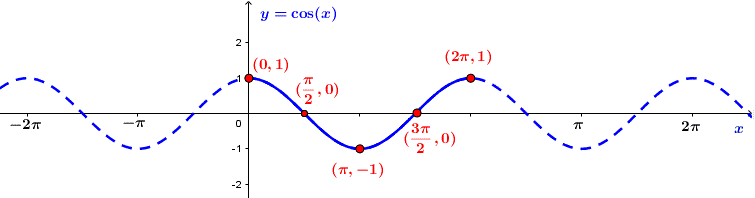
Hàm số lượng giác và đồ thị CTST

b) Hàm số y = cosx

- Tập xác định: D = \mathbb{R}

- Tập giá trị [-1; 1] hay - 1 \leqslant \operatorname{cosx} \leqslant 1,\forall x \in \mathbb{R}

- Hàm số là hàm chẵn tuần hoàn với chu kì T = 2\pi

- Đồng biến trên mỗi khoảng \left( { - \pi + k2\pi ;k2\pi } \right) và nghịch biến trên mỗi khoảng \left( {k2\pi ;\pi + k2\pi } \right), k \in \mathbb{Z}

- Có đồ thị là một đường hình sin đối xứng qua trục tung.

Đồ thị hàm số y = \cos x

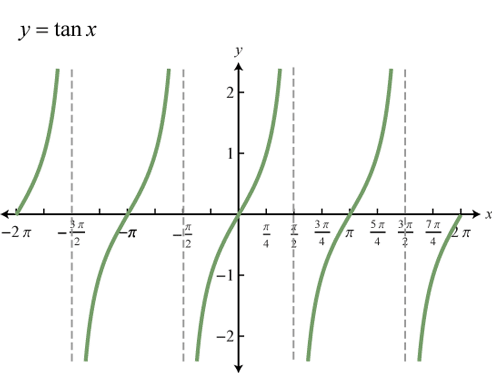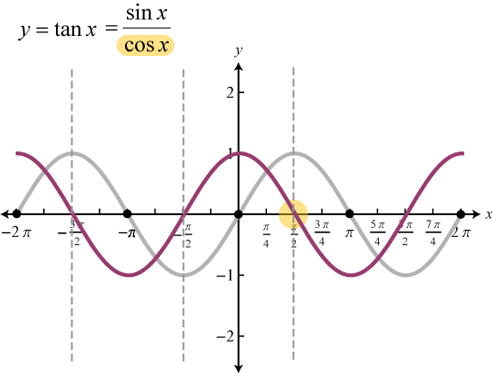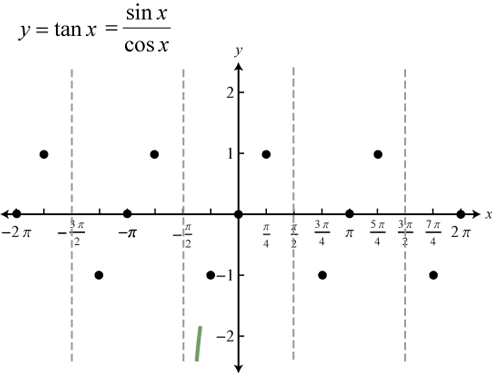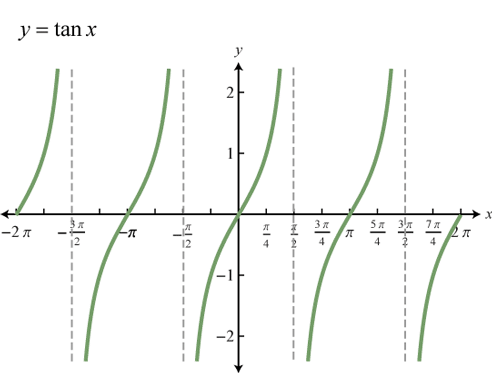
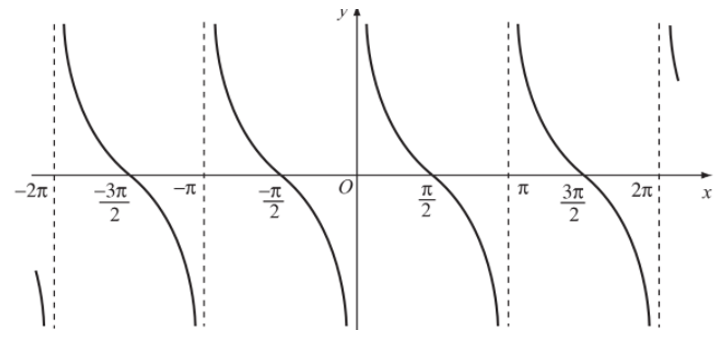
Hàm số lượng giác và đồ thị CTST

c) Hàm số y = tanx

- Tập xác định: D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}

- Tập giá trị: \mathbb{R}

- Hàm số là hàm lẻ tuần hoàn với chu kì T = \pi

- Đồng biến trên mỗi khoảng \left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)

- Có đồ thị đối xứng qua gốc tọa độ.

Đồ thị hàm số y = \tan x

Hàm số lượng giác và đồ thị CTST

d) Hàm số y = cotx

- Tập xác định: D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}

- Tập giá trị: \mathbb{R}

- Hàm số là hàm lẻ tuần hoàn với chu kì T = \pi

- Nghịch biến trên mỗi khoảng \left( {k\pi ;\pi + k\pi } \right),k \in \mathbb{Z}

- Có đồ thị đối xứng qua gốc tọa độ.

Đồ thị hàm số y = \cot x

Hàm số lượng giác và đồ thị CTST

 

  • 18 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11 CTST