Lớp 10 Toán 10 - Kết nối tri thức

Dấu của tam thức bậc hai

1. Dấu của tam thức bậc hai

  • Tam thức bậc hai là biểu thức có dạng f(x)=a{{x}^{2}}+bx+c(a\ne 0), a,b,c được gọi là các hệ số.
  • Nghiệm của phương trình bậc hai a{{x}^{2}}+bx+c=0 cũng được gọi là nghiệm của tam thức bậc hai a{{x}^{2}}+bx+c.

Cho tam thức bậc hai f(x)=a{{x}^{2}}+bx+c(a\ne 0). Ta có:

  • Nếu \Delta <0 thì f(x) cùng dấu với hệ số a với mọi x thuộc \mathbb{R}.
  • Nếu \Delta =0 thì f(x) cùng dấu với hệ số a với mọi x\ne -\frac{b}{2a} và f\left( -\frac{b}{2a} \right)=0.
  • Nếu \Delta >0 thì f(x) có hai nghiệm phân biệt {{x}_{1}};{{x}_{2}}({{x}_{1}}<{{x}_{2}}). Khi đó: f(x) cùng dấu với hệ số a với mọi x\in \left( -\infty ;{{x}_{1}} \right)\cup \left( {{x}_{2}};+\infty \right); f(x) trái dấu với hệ số a với mọi x\in \left( {{x}_{1}};{{x}_{2}} \right).

(Trong định lý trên, có thể thay \Delta bằng \Delta ').

Ví dụ:

Xét dấu các tam thức bậc hai sau:

a. {{x}^{2}}+x+2;

b. 2{{x}^{2}}+x-3.

Hướng dẫn giải

a. f(x)={{x}^{2}}+x+2 có \Delta =-7<0 và a=1>0 nên f(x)>0\,\,\forall x\in R.

b. g(x)=2{{x}^{2}}+x-3 có \Delta =25>0, a=2>0. g(x) có hai nghiệm phân biệt {x}_{1}=1,{x}_{2}=-\frac{3}{2}.

Bảng xét dấu:

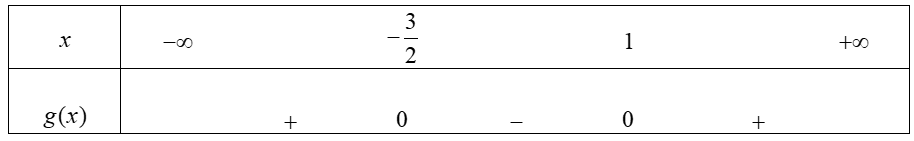
Suy ra g(x)>0\,\,\forall x\in \left( -\infty ;-\frac{3}{2} \right)\cup \left( \frac{3}{2};+\infty \right) và g(x)<0\,\,\forall x\in \left( -\frac{3}{2};1 \right).

2. Bất phương trình bậc hai

Bất phương trình bậc hai một ẩn là bất phương trình có một trong các dạng sau:

 a{x^2} + bx + c > 0{\mkern 1mu} {\rm{ }};{\mkern 1mu} a{x^2} + bx + c \ge 0{\mkern 1mu} ;{\mkern 1mu} a{x^2} + bx + c < 0{\mkern 1mu} ;{\mkern 1mu} a{x^2} + bx + c \le 0 với a\neq0.

  • Nghiệm của bất phương trình bậc hai một ẩn là các giá trị x mà khi thay vào bất phương trình thì ta được bất đẳng thức đúng.
  • Tập hợp tất cả các nghiệm của bất phương trình được gọi là tập nghiệm của bất phương trình.

Nhận xét:

  1. Để giải bất phương trình a{{x}^{2}}+bx+c>0\,(tương tự với các bất phương trình còn lại) thì ta cần xét dấu của tam thức a{{x}^{2}}+bx+c, từ đó suy ra tập nghiệm.
  2. Cho tam thức bậc hai f(x)=a{{x}^{2}}+bx+c (a\neq0). Đặt \Delta = {b^2} - 4ac, khi đó:
  • f(x) \ge 0{\mkern 1mu} {\mkern 1mu} \forall x \in R \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {\Delta \le 0}\\ {a > 0} \end{array}} \right.; f(x) > 0{\mkern 1mu} {\mkern 1mu} \forall x \in R \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {\Delta < 0}\\ {a > 0} \end{array}} \right..
  • f(x) \le 0{\mkern 1mu} {\mkern 1mu} \forall x \in R \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {\Delta \le 0}\\ {a < 0} \end{array}} \right.; f(x) < 0{\mkern 1mu} {\mkern 1mu} \forall x \in R \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {\Delta < 0}\\ {a < 0} \end{array}} \right..

Ví dụ 1: Giải bất phương trình 6{{x}^{2}}+7x-5>0.

Xét f(x)=6{{x}^{2}}+7x-5. Ta có: \Delta =169>0 và a=6>0. f(x)=0 có hai nghiệm phân biệt {{x}_{1}}=-\frac{5}{3} và {{x}_{2}}=\frac{1}{2}.

Bảng xét dấu:

Suy ra bất phương trình 6{{x}^{2}}+7x-5>0 có nghiệm khi x\in \left( -\infty ;-\frac{5}{3} \right)\cup \left( \frac{1}{2};+\infty \right).

Ví dụ 2: Tìm m để tam thức bậc hai sau dương với mọi x\in \mathbb{R}: 2{{x}^{2}}+(m-2)x+4-m.

Hướng dẫn giải

Đặt f(x)=2{{x}^{2}}+(m-2)x+4-m.

Ta có:f(x)>0 \forall x\in R\Leftrightarrow \left\{ \begin{matrix}\Delta <0 \\a>0 \\\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}{{(m-2)}^{2}}-4.2.(4-m)<0 \\2>0 \\\end{matrix} \right.

 

\Leftrightarrow {(m - 2)^2} - 8(4 - m) < 0\Leftrightarrow {m^2} + 4m - 28 < 0\Leftrightarrow - 2 - 4\sqrt 2 < m < - 2 + 4\sqrt 2

Vậy để tam thức bậc hai dương với mọi x\in \mathbb{R} thì - 2 - 4\sqrt 2 < m < - 2 + 4\sqrt 2.

Câu trắc nghiệm mã số: 7912,7914,7915,7916,7917,7919,7920,7921,7923,7976,7979,7982
  • 22 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 KNTT