Luyện tập Phương trình quy về phương trình bậc hai (Trung bình)

ĐK: x ∈ [5; 7]

Đặt t = x − 6 , t ∈ [ − 1; 1].

Phương trình trở thành .

Ta có VT(*) ≤ 4, VP(*) ≥ 4 nên (*) ⇔ VT(*) = VP(*) = 4 ⇔ t = 0 ⇒ x = 6(TM).

Vậy phương trình có một nghiệm.

Phương trình .

Vậy S = {2}.

ĐKXĐ: 2x(x²+1) ≥ 0 ⇔ x ≥ 0

Đặt , a  ≥ 0, b ≥ 0

Suy ra a² + b² = 2x + x² + 1 = (x+1)²

Phương trình trở thành a² + b² − 2ab = 0 ⇔ (a−b)² = 0 ⇔ a = b

Suy ra (thỏa mãn)

Vậy phương trình có một nghiệm là x = 1 .

Ta thấy không là nghiệm của phương trình

Xét , phương trình đã cho

Đến đây, chú ý

Nên phương trình có nghiệm phải thỏa mãn

Do đó phương trình đã cho

Nhưng x =  − 1 không thoả mãn nên phương trình có nghiệm x = 1

* TH2:

(thỏa mãn)

Vậy phương trình có nghiệm duy nhất x = 1.

ĐKXĐ: x ≥ 1 .

Chia cả hai vế cho ta có

Đặt

Phương trình trở thành  − 3t² + 2t = m (*)

Xét hàm số y =  − 3t² + 2t trên [0; 1) , ta có ,

Bảng biến thiên

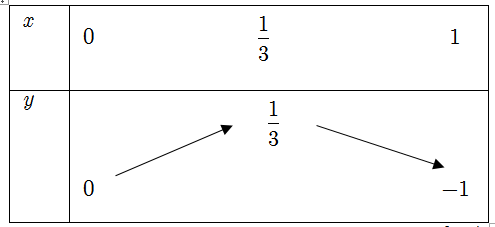
Phương trình ban đầu có nghiệm ⇔ phương trình (*) có nghiệm t∈ [0; 1)

⇔ đồ thị hàm số y =  − 3t² + 2t trên [0; 1) cắt đường thẳng

Vậy phương trình ban đầu có nghiệm khi và chỉ khi .

.

Vậy phương trình có một nghiệm.

Đặt (t≥0).Phương trình trở thành:

Với t = 1 ta được .

Vậy phương trình có hai nghiệm.

Xét phương trình: (1)

Điều kiện :

Thay x = 8 ta thấy (1) thoả mãn. Vậy, phương trình (1) có tập nghiệm là S = {8}.

ĐKXĐ: .

Thay x = 1 vào , ta được: .

Vậy phương trình vô nghiệm.

.

Vậy phương trình vô nghiệm.

.

Vậy S = {2;4}.

Xét phương trình:

Điều kiện:

Vậy phương trình vô nghiệm.

ĐKXĐ: x³ + 1 ≥ 0 ⇔ x ≥  − 1.

Phương trình

Đặt , a ≥ 0,  b ≥ 0

Suy ra a² + b² = x² + 2 khi đó

Phương trình trở thành

Với 3a = b ta có

(thỏa mãn điều kiện)

Với a = 3b ta có

 ⇔ 9x² − 10x + 8 = 0 (phương trình vô nghiệm).

Vậy phương trình có nghiệm là .

ĐK:

.

Đặt , (t≥0)Phương trình thành .

t = 1 ⇒ x² − 2x − 1 = 0

.

Vậy phương trình đã cho có hai nghiệm là .

Xét phương trình:

Điều kiện: .

Vậy phương trình vô nghiệm.

Ta có

.

Tổng các bình phương của các nghiệm của phương trình là .

Ta thấy x =  − 3 không là nghiệm của phương trình.

Xét x ≠  − 3, phương trình

Phương trình (*)

(thỏa mãn)

Vậy phương trình đã cho có hai nghiệm x = 0 và .

Đặt . Phương trình trở thành:

t³ − 2t + 4 = 0 ⇔ (t+2)(t²−2t+2) = 0 ⇔ t =  − 2

Ta được

.

Tổng các nghiệm của phương trình là  − 5.

ĐK x > 2

.

Phương trình (1) có nghiệm duy nhất .