Vectơ trong mặt phẳng tọa độ
1. Tọa độ của vectơ
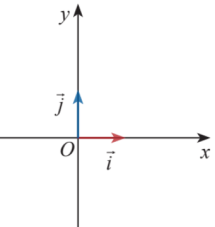
Cho hệ trục ![]() , ta có:
, ta có:
- Vectơ đơn vị của trục hoành là

- Vectơ đơn vị của trục tung là

- Với mỗi vectơ
 , ta luôn có:
, ta luôn có:  . Trong đó
. Trong đó  được gọi là hoành độ, tung độ của
được gọi là hoành độ, tung độ của  .
. - Cho hai điểm
 và
và  , khi đó
, khi đó  .
. - Hai vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau, tức là:
![]()
2. Biểu thức tọa độ của các phép toán vectơ
Cho hai vectơ ![]() . Khi đó:
. Khi đó:
 .
. với
với  .
.
Nhận xét:
- Hai vectơ
 cùng phương khi và chỉ khi
cùng phương khi và chỉ khi  . (điều kiện
. (điều kiện  )
) - Nếu điểm
 có tọa độ
có tọa độ  thì vectơ
thì vectơ  và có độ dài
và có độ dài  .
. - Vectơ
 cũng có độ dài
cũng có độ dài  .
. - Cho
 thì độ dài đoạn thẳng
thì độ dài đoạn thẳng  .
.
Chú ý:
- Trung điểm
 của đoạn thẳng
của đoạn thẳng  có tọa độ là:
có tọa độ là:  .
. - Trọng tâm
 của tam giác
của tam giác  có tọa độ là:
có tọa độ là:  .
.
Ví dụ 1: Trong mặt phẳng tọa độ ![]() , cho
, cho ![]() .
.
a) Tìm tọa độ trọng tâm ![]() của tam giác
của tam giác ![]() .
.
b) Tìm ![]() sao cho tứ giác
sao cho tứ giác ![]() là hình bình hành.
là hình bình hành.
Hướng dẫn giải
a) Ta có: ![]() .
.
Suy ra ![]() .
.
b) Vì tứ giác ![]() là hình bình hành nên
là hình bình hành nên ![]() .
.
Áp dụng công thức tính tọa độ vectơ khi biết hai điểm, ta có: ![]() và
và ![]() .
.
Ta có:![]()
![]()
![]() .
.
Vậy ![]() .
.
Ví dụ 2: Trong mặt phẳng tọa độ ![]() , cho
, cho ![]() . Tính độ dài đoạn thẳng
. Tính độ dài đoạn thẳng ![]() và tìm tọa độ trung điểm
và tìm tọa độ trung điểm ![]() của
của ![]() .
.
Hướng dẫn giải
Áp dụng công thức tính độ dài đoạn thẳng, ta có:
![]()
![]() .
.
Trung điểm ![]() của có tọa độ thỏa mãn:
của có tọa độ thỏa mãn:
![]() . Suy ra
. Suy ra ![]() .
.
Ví dụ 3: Trong mặt phẳng tọa độ ![]() , cho
, cho ![]() . Tìm
. Tìm ![]() để ba điểm
để ba điểm ![]() thẳng hàng.
thẳng hàng.
Hướng dẫn giải
Ta có: ![]() và
và ![]() .
.
Để ba điểm ![]() thẳng hàng thì:
thẳng hàng thì: ![]() .
.
Vậy để ![]() thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.
Sắp xếp theo
Xóa
Gửi bình luận
-
Chương 1: Mệnh đề và tập hợp
-
Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
-
Chương 3: Hệ thức lượng trong tam giác
-
Chương 4: Vectơ
-
Chương 5: Các số đặc trưng của mẫu số liệu không ghép nhóm
-
Đề thi học kì 1
-
Chương 6: Hàm số, đồ thị và ứng dụng
-
Chương 7: Phương pháp tọa độ trong mặt phẳng
-
Đề thi giữa học kì 2
-
Chương 8: Đại số tổ hợp
-
Chương 9: Tính xác suất theo định nghĩa cổ điển
-
Đề thi học kì 2







