Tích của vectơ với một số

1. Tích của một số với một vectơ

Quy ước: và .

Nhận xét:

• và .
• là trung điểm đoạn thẳng thì (với điểm tùy ý).
• là trọng tâm tam giác thì (với điểm tùy ý).

2. Tính chất

Với hai vectơ bất kì và mọi số thực ta có:

3. Điều kiện để hai vectơ cùng phương

Ví dụ 1: Cho hình bình hành . Gọi là trung điểm . Hãy biểu thị vectơ theo hai vectơ và .

Hướng dẫn giải

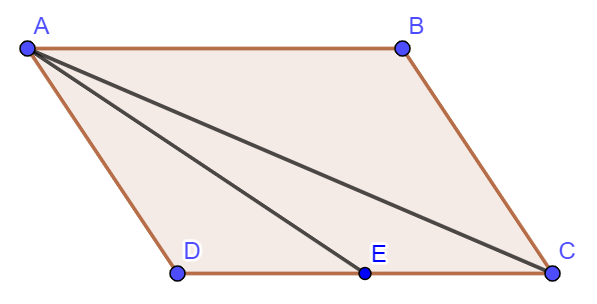
Vì là trung điểm nên hay .

Áp dụng quy tắc hình bình hành: .

Do đó: .

Ví dụ 2: Cho tam giác có lần lượt là trung điểm . Chứng minh:

a) ;

b) .

Hướng dẫn giải

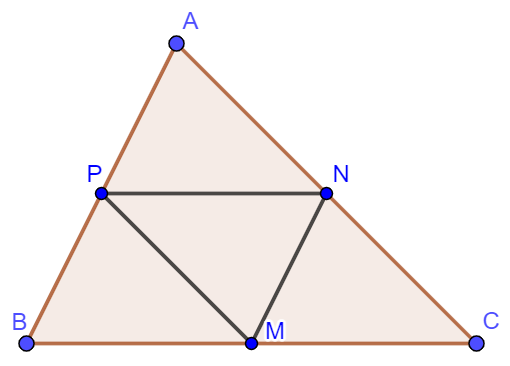
a) Ta có: (Vì ).

b) Ta có: (Vì là đường trung bình trong tam giác nên ).

Ví dụ 3: Cho tam giác . Hãy tìm các điểm thỏa mãn:

a) ;

b) .

Hướng dẫn giải

a) (2 vectơ ngược hướng).

Suy ra điểm nằm giữa đoạn thẳng sao cho . 

Hình vẽ biểu diễn điểm :

b)

(2 vectơ cùng hướng).

Suy ra điểm nằm giữa đoạn sao cho .

Hình vẽ biểu diễn điểm :