Đồ thị của hàm số nào sau đây là parabol có đỉnh I(−1; 3).
Đỉnh Parabol là .
Do đó chỉ có đáp án y = 2x2 + 4x + 5 thỏa mãn.
Hãy cùng Luyện tập bài Hàm số bậc hai các em nhé!
Đồ thị của hàm số nào sau đây là parabol có đỉnh I(−1; 3).
Đỉnh Parabol là .
Do đó chỉ có đáp án y = 2x2 + 4x + 5 thỏa mãn.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ − 7; 7] để phương trình mx2 − 2(m+2)x + m − 1 = 0 có hai nghiệm phân biệt?
TH1:; phương trình chỉ có một nghiệm duy nhất nên loại m = 0
TH2: m ≠ 0
Để mx2 − 2(m+2)x + m − 1 = 0với m ∈ [ − 7; 7]có hai nghiệm phân biệt thì
đồng thời m ∈ [ − 7; 7].
Vậy m = {1; 2;3;4;5;6;7}→ có 7 giá trị nguyên của m thỏa mãn.
Parabol y = − x2 + 2x + 3 có phương trình trục đối xứng là
Parabol y = − x2 + 2x + 3 có trục đối xứng là đường thẳng ⇔ x = 1.
Trục đối xứng của parabol y = − x2 + 5x + 3 là đường thẳng có phương trình
Trục đối xứng của parabol y = ax2 + bx + c là đường thẳng .
Trục đối xứng của parabol y = − x2 + 5x + 3 là đường thẳng .
Cho parabol (P) : y = x2 − 4x + 3 và đường thẳng d : y = mx + 3. Tìm tất cả các giá trị thực của m để d cắt (P) tại hai điểm phân biệt A, B sao cho diện tích tam giác OAB bằng ![]() .
.
Phương trình hoành độ giao điểm của (P) và d là x2 − 4x + 3 = mx + 3
.
Để d cắt (P) tại hai điểm phân biệt A, B khi và chỉ khi 4 + m ≠ 0 ⇔ m ≠ − 4.
Với .
Với .
Gọi H là hình chiếu của B lên OA. Suy ra BH = |xB| = |4+m|.
Theo giả thiết bài toán, ta có
.
Giá trị lớn nhất của hàm số ![]() bằng:
bằng:
Ta có
Vậy giá trị lớn nhất của hàm số bằng
.
Cho hàm số f(x) = ax2 + bx + c đồ thị như hình bên. Hỏi với những giá trị nào của tham số thực m thì phương trình |f(x)| = m có đúng 4 nghiệm phân biệt.
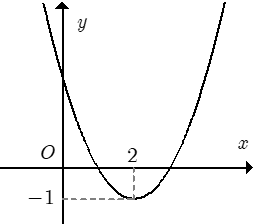
Ta có . Từ đó suy ra cách vẽ đồ thị hàm số (C) từ đồ thị hàm số y = f(x) như sau:
Giữ nguyên đồ thị y = f(x) phía trên trục hoành.
Lấy đối xứng phần đồ thị y = f(x) phía dưới trục hoành qua trục hoành ( bỏ phần dưới ).
Kết hợp hai phần ta được đồ thị hàm số y = |f(x)| như hình vẽ.
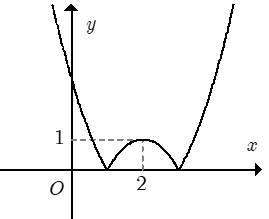
Phương trình |f(x)| = m là phương trình hoành độ giao điểm của đồ thị hàm số y = |f(x)| và đường thẳng y = m (song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có ycbt ⇔ 0 < m < 1.
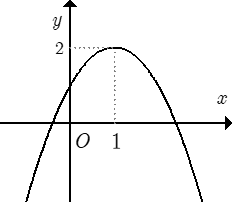
Đồ thị hình bên dưới là đồ thị của hàm số nào?
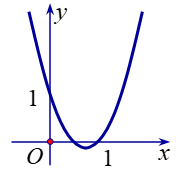
Đồ thị cắt trục tung tại điểm có tung độ bằng 1.
Đồ thị cắt trục hoành tại điểm có hoành độ bằng 1, phương trình hoành độ giao điểm phải có nghiệm x = 1, ta chỉ có phương trình .
Tìm khẳng định đúng trong các khẳng định sau?
* Theo định nghĩa tam thức bậc hai thì f(x) = 3x2 + 2x − 5 là tam thức bậc hai.
Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng [ − 10; − 4) để đường thẳng d : y = − (m+1)x + m + 2 cắt Parabol (P) : y = x2 + x − 2 tại hai điểm phân biệt cùng phía với trục tung?
Xét phương trình: − (m+1)x + m + 2 = x2 + x − 2 ⇔ x2 + x(m+2) − m − 4 = 0
Để đường thẳng d cắt Parabol(P) tại hai điểm phân biệt cùng phía với trục tung vậy điều kiện là
Vậy trong nửa khoảng[ − 10; − 4) có 6 giá trị nguyên m.
Biết rằng hàm số y = ax2 + bx + c(a≠0) đạt giá trị lớn nhất bằng ![]() tại
tại ![]() và tổng lập phương các nghiệm của phương trình y = 0 bằng 9. Tính P = abc.
và tổng lập phương các nghiệm của phương trình y = 0 bằng 9. Tính P = abc.
Hàm số y = ax2 + bx + c(a≠0) đạt giá trị lớn nhất bằng tại
nên ta có
và điểm
thuộc đồ thị
Gọi x1, x2 là hai nghiệm của phương trình y = 0. Theo giả thiết: x13 + x23 = 9
.
Từ đó ta có hệ
Một chiếc cổng hình parabol có phương trình ![]() . Biết cổng có chiều rộng d = 5 mét (như hình vẽ). Hãy tính chiều cao h của cổng.
. Biết cổng có chiều rộng d = 5 mét (như hình vẽ). Hãy tính chiều cao h của cổng.
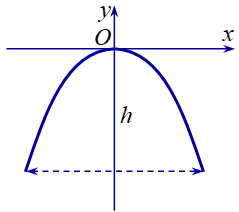
Gọi Avà Blà hai điểm ứng với hai chân cổng như hình vẽ.
Vì cổng hình parabol có phương trình và cổng có chiều rộng d = 5 mét nên:
AB = 5 và .
Vậy chiều cao của cổng làmét.
Cho hàm số f(x) = ax2 + bx + c có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + m − 2018 = 0 có duy nhất một nghiệm.
Phương trình Đây là phương trình hoành độ giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = 2018 − m (có phương song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có ycbt 2018 − m = 2 ⇔ m = 2016.
Biết đường thẳng d : y = mx cắt Parabol (P) : y = x2 − x + 1 tại hai điểm phân biệt A, B. Khi đó tọa độ trung điểm I của đoạn thẳng AB là
Xét phương trình hoành độ giao điểm của d và (P):
mx = x2 − x + 1 ⇔ x2 − (m+1)x + 1 = 0
Vì hoành độ giao điểm xA, xB là hai nghiệm của phương trình nên ta có tọa độ trung điểm I là
.
Tìm tất cả các giá trị thực của tham số m để phương trình x2 − 5x + 7 + 2m = 0 có nghiệm thuộc đoạn [1; 5].
Ta có x2 − 5x + 7 + 2m = 0 ⇔ x2 − 5x + 7 = − 2m. (*)
Phương trình (*) là phương trình hoành độ giao điểm của parabol (P) : x2 − 5x + 7 và đường thẳng y = − 2m (song song hoặc trùng với trục hoành).
Ta có bảng biến thiên của hàm số y = x2 − 5x + 7 trên [1; 5] như sau:
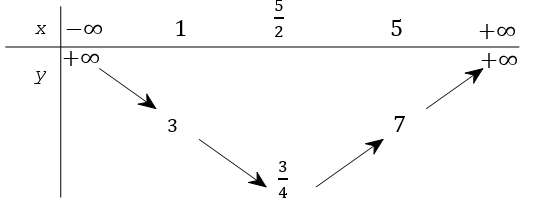
Dựa vào bảng biến ta thấy x ∈ [1; 5] thì .
Do đo để phương trình (*) có nghiệm
Xác định parabol (P): y = ax2 + bx + c, a ≠ 0 biết (P) cắt trục tung tại điểm có tung độ bằng 1 và có giá trị nhỏ nhất bằng ![]() khi
khi ![]() .
.
Ta có (P) cắt trục tung tại điểm có tung độ bằng 1: Khi x = 0 thì y = 1 ⇒ c = 1.
(P)có giá trị nhỏ nhất bằng khi
nên:
⇔
.
Vậy (P): y = x2 − x + 1.
Tìm parabol (P) : y = ax2 + 3x − 2, biết rằng parabol có trục đối xứng x = − 3.
Trục đối xứng của (P) có dạng:
.
Vậy (P) có phương trình: .
Tìm tất cả các giá trị thực của m để phương trình x4 − 2x2 + 3 − m = 0 có nghiệm.
Đặt t = x2 (t≥0).
Khi đó, phương trình đã cho trở thành: t2 − 2t + 3 − m = 0. (*)
Để phương trình đã cho có nghiệm khi và chỉ khi (*) có nghiệm không âm.
Phương trình (*) vô nghiệm khi và chỉ khi Δ′ < 0 ⇔ m − 2 < 0 ⇔ m < 2.
Phương trình (*) có 2 nghiệm âm khi và chỉ khi .
Do đó, phương trình (*) có nghiệm không âm khi và chỉ khi m ≥ − 2.
Cho hai hàm số y1 = x2 + (m−1)x + m, y2 = 2x + m + 1. Khi đồ thị hai hàm số cắt nhau tại hai điểm phân biệt thì m có giá trị là
Phương trình hoành độ giao điểm: x2 + (m−1)x + m = 2x + m + 1 ⇔ x2 + (m−3)x − 1 = 0 (1).
Khi đồ thị hai hàm số cắt nhau tại hai điểm phân biệt thì pt(1) có hai nghiệm phân biệt
⇔ Δ = (m−3)2 + 4 > 0 luôn đúng ∀m ∈ ℝ.
