Lớp 10 Toán 10 - Kết nối tri thức

Giá trị lượng giác của một góc từ 0 đến 180 độ

1. Giá trị lượng giác

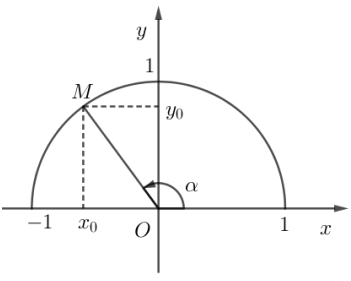
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành có bán kính R=1 được gọi là nửa đường tròn đơn vị.

Với mỗi góc \alpha (0^{\circ} \le \alpha \le 180^{\circ}) ta xác định một điểm M trên nửa đường tròn đơn vị sao cho \widehat {xOM} = \alpha và điểm M có tọa độ M(x_0;y_0). Khi đó:

  • \sin của góc \alpha là y_0, kí hiệu \sin \alpha = {y_0}.
  • côsin của góc \alpha là x_0, kí hiệu \cos \alpha =x_0.
  • tang của góc \alpha là \frac{y_0}{x_0} (x_0 \neq 0), kí hiệu \tan \alpha = \frac{y_0}{x_0}.
  • côtang của góc \alpha là \frac {x_0}{y_0} (y_0 \neq 0), kí hiệu \cot \alpha = \frac {x_0}{y_0}.

Các số \sin \alpha ; \cos \alpha; \tan \alpha ; \cot \alpha là các giá trị lượng giác của góc \alpha.

2. Quan hệ giữa các giá trị lượng giác bù nhau

  • \sin \alpha = \sin (180^{\circ} -\alpha)
  • \cos \alpha = -\cos (180^{\circ} -\alpha)
  • \tan \alpha = -\tan (180^{\circ} -\alpha)
  • \cot \alpha = -\cot (180^{\circ} -\alpha)

Ví dụ: Đơn giản hóa các biểu thức sau:

a) \sin 110^{\circ} +\cos 50^{\circ} -\sin70^{\circ} +\cos130^{\circ};

b) -2\sin (180^{\circ} -\beta).\cot \beta + 3\cos \beta +\cos(180^{\circ} -\beta).

Hướng dẫn giải

a) \sin 110^{\circ} +\cos 50^{\circ} -\sin70^{\circ} +\cos130^{\circ}= (\sin 110^{\circ} -\sin70^{\circ}) +(\cos130^{\circ}+\cos 50^{\circ})= (\sin (180^\circ - 110^{\circ}) -\sin70^{\circ})+(\cos130^{\circ}-\cos (180^{\circ} -50^{\circ}))=(\sin 70^{\circ} -\sin 70^{\circ} )+(\cos 130^{\circ} -\cos 130^{\circ} )=0.

b) -2\sin (180^{\circ} -\beta).\cot \beta + 3\cos \beta +\cos(180^{\circ} -\beta)=-2\sin \beta.\cot \beta + 3\cos \beta -\cos\beta-2\sin \beta. \frac {\cos\beta} {\sin \beta} + 3\cos \beta -\cos\beta =-2\cos\beta + 3\cos \beta -\cos\beta=0.

3. Giá trị lượng giác của các góc đặc biệt

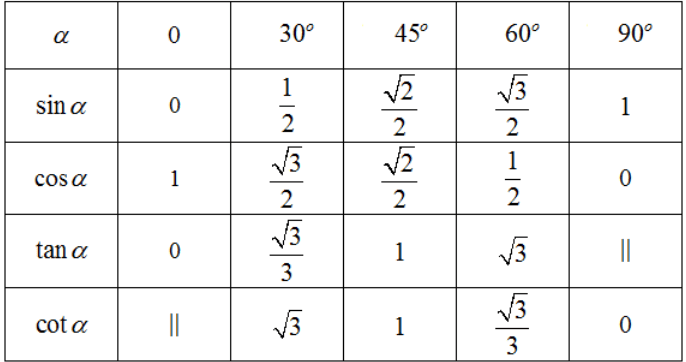
Chú ý: Trong bảng trên, kí hiệu || để chỉ các giá trị lượng giác không xác định.

 

Ví dụ: Cho góc \alpha (0^{\circ} < \alpha <180^{\circ}) thỏa mãn \tan \alpha =2. Hãy tính giá trị biểu thức S= \frac {3\sin\alpha +2\cos\alpha}{2\sin\alpha -3\cos\alpha}.

Hướng dẫn giải

Vì \tan \alpha =\frac {\sin\alpha}{\cos\alpha} nên:

Chia cả tử cả mẫu cho \cos\alpha, ta được: S= \frac {3\tan\alpha +2}{2\tan\alpha -3}= \frac {3.2+2}{2.2 -3}=8.

 

 

  • 24 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 KNTT